题目内容
11.一水池水深H=3m,现从水面上方h=1.8m高处由静止释放一个硬质小球,测得小球从释放到落至水池底部用时t=1.1s.已知小球直径远小于水池深度,不计空气及水的阻力,进入水池过程中浮力变化不计,取g=10m/s2,求:(1)小球在水中运动的时间和加速度;
(2)从水面上方多高处由静止释放小球,才能使小球从释放到落至池底所用时间最短.
分析 (1)通过空中自由落体的时间,求出在水中运动的时间,根据落水的速度、在水中运动的时间、位移,求出在水中运动的加速度,即可分析小球在水中的运动情况.
(2)列出下落总时间与水面上方高度的关系式,通过数学方法求极小值.
解答 解:(1)水面上 $h=\frac{1}{2}g{t}_{1}^{2}$ ①
解得${t}_{1}^{\;}=0.6$s
设水中做匀变速运动的加速度为a,时间为${t}_{2}^{\;}$,则${t}_{2}^{\;}=t-{t}_{1}^{\;}=0.5$s ②
$H=(g{t}_{1}^{\;}){t}_{2}^{\;}+\frac{1}{2}a{t}_{2}^{2}$ ③
解得a=0,即水中做匀速直线运动
(2)设释放点距水面x,则
总时间${t}_{x}^{\;}=\sqrt{\frac{2x}{g}}+\frac{H}{\sqrt{2gx}}$④
当$\sqrt{\frac{2x}{g}}=\frac{H}{\sqrt{2gx}}$时,即$x=\frac{H}{2}$=1.5m
答:(1)小球在水中运动的时间0.6s和加速度为0;
(2)从水面上方1.5m处由静止释放小球,才能使小球从释放到落至池底所用时间最短
点评 解决本题要掌握自由落体运动的位移公式,速度公式求时间求速度.关键要能运用数学知识求解时间最短的条件.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
1.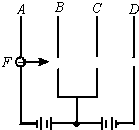 如图所示,从P处释放一个无初速度的电子向B板方向运动,指出下列对电子运动的描述中哪项是正确的(设电源电动势E)( )
如图所示,从P处释放一个无初速度的电子向B板方向运动,指出下列对电子运动的描述中哪项是正确的(设电源电动势E)( )
 如图所示,从P处释放一个无初速度的电子向B板方向运动,指出下列对电子运动的描述中哪项是正确的(设电源电动势E)( )
如图所示,从P处释放一个无初速度的电子向B板方向运动,指出下列对电子运动的描述中哪项是正确的(设电源电动势E)( )| A. | 电子到达B板时的动能是Ee | B. | 电子从B板到达C板动能变化量为零 | ||
| C. | 电子到达D板时动能是2Ee | D. | 电子在A板和D板之间做往复运动 |
2.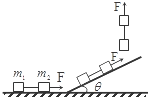 如图所示,质量为m1和m2的两个材料相同的物体用细线相连,在大小恒定的拉力F作用下,先沿水平面,再沿斜面,最后竖直向上匀加速运动,不计空气阻力,在三个阶段的运动中,线上拉力的大小( )
如图所示,质量为m1和m2的两个材料相同的物体用细线相连,在大小恒定的拉力F作用下,先沿水平面,再沿斜面,最后竖直向上匀加速运动,不计空气阻力,在三个阶段的运动中,线上拉力的大小( )
 如图所示,质量为m1和m2的两个材料相同的物体用细线相连,在大小恒定的拉力F作用下,先沿水平面,再沿斜面,最后竖直向上匀加速运动,不计空气阻力,在三个阶段的运动中,线上拉力的大小( )
如图所示,质量为m1和m2的两个材料相同的物体用细线相连,在大小恒定的拉力F作用下,先沿水平面,再沿斜面,最后竖直向上匀加速运动,不计空气阻力,在三个阶段的运动中,线上拉力的大小( )| A. | 由大变小 | B. | 由小变大 | ||
| C. | 始终不变且大小为$\frac{m}{{m}_{1}+{m}_{2}}$F | D. | 由大变小再变大 |
19. 滑板A放在光滑水平面上,质量为M,质量为m的滑块B(可视为质点)放在滑板右端,滑块与滑板间动摩擦因数为μ,滑板和滑块均静止.现对滑板施加向右的水平恒力F,滑块从滑板右端滑到左端的时间为t.下列判断正确的是( )
滑板A放在光滑水平面上,质量为M,质量为m的滑块B(可视为质点)放在滑板右端,滑块与滑板间动摩擦因数为μ,滑板和滑块均静止.现对滑板施加向右的水平恒力F,滑块从滑板右端滑到左端的时间为t.下列判断正确的是( )
 滑板A放在光滑水平面上,质量为M,质量为m的滑块B(可视为质点)放在滑板右端,滑块与滑板间动摩擦因数为μ,滑板和滑块均静止.现对滑板施加向右的水平恒力F,滑块从滑板右端滑到左端的时间为t.下列判断正确的是( )
滑板A放在光滑水平面上,质量为M,质量为m的滑块B(可视为质点)放在滑板右端,滑块与滑板间动摩擦因数为μ,滑板和滑块均静止.现对滑板施加向右的水平恒力F,滑块从滑板右端滑到左端的时间为t.下列判断正确的是( )| A. | 滑块与滑板间动摩擦因数应满足$μ<\frac{F}{Mg}$ | |
| B. | 若仅减小M,时间t会缩短 | |
| C. | 若仅减小m,时间t会缩短 | |
| D. | 若仅减小F,时间t会缩短 | |
| E. | 若在滑板A右端与B平齐地再放一个同样的滑块C,则两滑块在滑板上的运动时间t不变 |
6. 如图所示,质量为m的球置于斜面上,被一个竖直挡板挡住.现用一个恒力F拉斜面,使斜面在水平面上向右做加速度为a的匀加速直线运动,忽略一切摩擦,以下说法中正确的是( )
如图所示,质量为m的球置于斜面上,被一个竖直挡板挡住.现用一个恒力F拉斜面,使斜面在水平面上向右做加速度为a的匀加速直线运动,忽略一切摩擦,以下说法中正确的是( )
 如图所示,质量为m的球置于斜面上,被一个竖直挡板挡住.现用一个恒力F拉斜面,使斜面在水平面上向右做加速度为a的匀加速直线运动,忽略一切摩擦,以下说法中正确的是( )
如图所示,质量为m的球置于斜面上,被一个竖直挡板挡住.现用一个恒力F拉斜面,使斜面在水平面上向右做加速度为a的匀加速直线运动,忽略一切摩擦,以下说法中正确的是( )| A. | 若加速度足够小,竖直挡板对球的弹力可能为零 | |
| B. | 若加速度足够大,斜面对球的弹力可能为零 | |
| C. | 斜面对球的弹力大小与加速度大小无关 | |
| D. | 挡板对球的弹力大小与加速度大小无关 |
16. 如图所示,木板静止于水平地面上,在其最右端放一可视为质点的木块.已知木块的质量m=1kg,木板的质量M=4kg,长L=2.5m,下表面与地面之间的动摩擦因数μ1=0.2,上表面与木块之间的动摩擦因数为μ2.现用水平恒力F拉木板,g取10m/s2.下列说法正确的是( )
如图所示,木板静止于水平地面上,在其最右端放一可视为质点的木块.已知木块的质量m=1kg,木板的质量M=4kg,长L=2.5m,下表面与地面之间的动摩擦因数μ1=0.2,上表面与木块之间的动摩擦因数为μ2.现用水平恒力F拉木板,g取10m/s2.下列说法正确的是( )
 如图所示,木板静止于水平地面上,在其最右端放一可视为质点的木块.已知木块的质量m=1kg,木板的质量M=4kg,长L=2.5m,下表面与地面之间的动摩擦因数μ1=0.2,上表面与木块之间的动摩擦因数为μ2.现用水平恒力F拉木板,g取10m/s2.下列说法正确的是( )
如图所示,木板静止于水平地面上,在其最右端放一可视为质点的木块.已知木块的质量m=1kg,木板的质量M=4kg,长L=2.5m,下表面与地面之间的动摩擦因数μ1=0.2,上表面与木块之间的动摩擦因数为μ2.现用水平恒力F拉木板,g取10m/s2.下列说法正确的是( )| A. | 若μ2=0,F=20 N,为了使木块能够滑离木板,则F作用的最短时间为1s | |
| B. | 若μ2=0,F=20 N,为了使木块尽快滑离木板,则F作用的最短时间为2s | |
| C. | 若μ2=0.3,为了能抽出木板,则F至少为25N | |
| D. | 若μ2=0.3,F=30 N且一直作用在木板上,则木块滑离木板需要的时间2s |
 如图,用两根绳子把质量为10千克的物体W吊在水平杆子AB上,∠ACW=150°,∠BCW=120°,如果绳子的质量忽略不计,求A处和B处所受力的大小.
如图,用两根绳子把质量为10千克的物体W吊在水平杆子AB上,∠ACW=150°,∠BCW=120°,如果绳子的质量忽略不计,求A处和B处所受力的大小. 为了减少汽车刹车失灵造成的危害,如图所示为高速路上在下坡路段设置的可视为斜面的紧急避险车道.一辆货车在倾角θ=30°的连续长直下坡高速路上,以v0=7m/s的速度在刹车状态下匀速行驶(在此过程及后面过程中,可认为发动机不提供牵引力),突然汽车刹车失灵,形如加速运动,此时汽车所受到的摩擦和空气阻力共为车重的0.2.在加速前进了x0=96m,货车冲上了平滑连接的倾角α=53°避险车道,已知货车在避险车道上所受到的摩擦和空气阻力共为车重的0.45.货车的各个运动过程均可视为直线运动.取
为了减少汽车刹车失灵造成的危害,如图所示为高速路上在下坡路段设置的可视为斜面的紧急避险车道.一辆货车在倾角θ=30°的连续长直下坡高速路上,以v0=7m/s的速度在刹车状态下匀速行驶(在此过程及后面过程中,可认为发动机不提供牵引力),突然汽车刹车失灵,形如加速运动,此时汽车所受到的摩擦和空气阻力共为车重的0.2.在加速前进了x0=96m,货车冲上了平滑连接的倾角α=53°避险车道,已知货车在避险车道上所受到的摩擦和空气阻力共为车重的0.45.货车的各个运动过程均可视为直线运动.取 如图,在宽为l,足够长的水平虚线内有垂直纸面向里的匀强磁场,其上方距上边界h处有一导线框(各边长如图中标注),现将导线框由静止释放,从线框下边进入磁场开始计时至线框完全离开磁场(整个过程线框保持竖直且不翻转).该过程中v-t图线可能正确的是( )
如图,在宽为l,足够长的水平虚线内有垂直纸面向里的匀强磁场,其上方距上边界h处有一导线框(各边长如图中标注),现将导线框由静止释放,从线框下边进入磁场开始计时至线框完全离开磁场(整个过程线框保持竖直且不翻转).该过程中v-t图线可能正确的是( )


