题目内容
16.如图所示的是四种电容式传感器: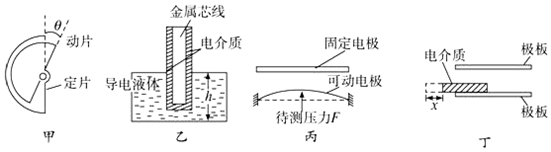
(1)图甲是测θ大小的电容式传感器,原理是θ变化,引起正对面积变化,从而引起C变化,由C可确定θ大小;
(2)图乙是测高度h的电容式传感器,原理是高度h变化,引起两极面积变化,相应C变化,由C可确定h大小;
(3)图丙是测压力F的电容式传感器,原理是压力F增加,造成两电极距离d减小,相应C变化,由C可确定F大小;
(4)图丁是测极板长度L的电容式传感器,原理是极板长度L变化,造成相应C变化,由C可确定L大小.
分析 电容器的决定式C=$\frac{?s}{4πkd}$,当电容器两极间正对面积变化时会引起电容的变化,其他条件不变的情况下成正比.
解答 解:(1)、图示电容器为可变电容器,通过转动动片改变正对面积,改变电容,可以用来测量角度θ 大小,其原理是θ 变化,引起正对面积变化,从而引起C变化,由C可确定 θ 大小.
(2)、图示电容器的一个极板时金属芯线,另一个极板是导电液,液面高度的变化影响电容器的正对面积,故是通过改变电容器两极间正对面积而引起电容变化的,可以用来测量液面的高度h,因此其原理是高度h变化,引起两极面积变化,相应C变化,由C可确定h大小;
(3)、丙图是通过改变极板间的距离,改变电容器的,而对极板的压力的大小能改变可变电极与另一个极板之间的距离,所以可以用来测量压力F,其原理是压力 F 增加,造成两电极距离 d 减小,相应C变化,由C可确定 F 大小;
(4)、可变电容器,通过改变电介质的位置,改变电容,所以可以用来测量极板长度 L,其原理是极板长度 L 变化,造成相应C变化,由C可确定 L 大小;
故答案为:(1)θ 大小;θ 变化,引起正对面积变化,从而引起C变化,由C可确定 θ 大小;
(2)高度h;高度h变化,引起两极面积变化,相应C变化,由C可确定h大小;
(3)压力 F;压力 F 增加,造成两电极距离 d 减小,相应C变化,由C可确定 F 大小;
(4)极板长度 L;极板长度 L 变化,造成相应C变化,由C可确定 L 大小.
点评 该题结合传感器的电路的特点来考查了影响电容器电容的因素,解答的关键是掌握如何改变电容器的电容,以及电容传感器的特点.

练习册系列答案
相关题目
4.关于洛伦兹力,以下说法正确的是( )
| A. | 带电粒子在磁场中一定会受到洛伦兹力的作用 | |
| B. | 若带电粒子在某点不受洛伦兹力,则该点的磁感应强度一定为零 | |
| C. | 洛伦兹力不改变运动电荷的速度 | |
| D. | 仅受洛伦兹力作用的运动电荷,动能一定不改变 |
5.哪位科学家终于在1831年发现了电磁感应现象,进一步揭示了电现象与磁现象之间的密切联系,奏响了电气化时代的序曲( )
| A. | 法拉第 | B. | 奥斯特 | C. | 爱迪生 | D. | 斯旺 |
2. 如图所示为一绕地球运行的人造地球卫星运行轨迹,卫星近地点P近似认为贴近地球表面,远地点Q距地面的高度为h,已知地球半径为R,地球表面重力加速度为g,则( )
如图所示为一绕地球运行的人造地球卫星运行轨迹,卫星近地点P近似认为贴近地球表面,远地点Q距地面的高度为h,已知地球半径为R,地球表面重力加速度为g,则( )
 如图所示为一绕地球运行的人造地球卫星运行轨迹,卫星近地点P近似认为贴近地球表面,远地点Q距地面的高度为h,已知地球半径为R,地球表面重力加速度为g,则( )
如图所示为一绕地球运行的人造地球卫星运行轨迹,卫星近地点P近似认为贴近地球表面,远地点Q距地面的高度为h,已知地球半径为R,地球表面重力加速度为g,则( )| A. | 该卫星的运动周期为2π$\sqrt{\frac{(R+\frac{h}{2})^{2}}{g{R}^{2}}}$ | |
| B. | 该卫星的发射速度大于第一宇宙速度 | |
| C. | 该卫星在P点的速度大小为$\sqrt{gR}$ | |
| D. | 该卫星在P点的加速度大于地球表面的重力加速度g |
3. 如图所示,a、b是截面为等腰直角三角形的两个相同的楔形物体,分别在垂直于斜边的大小相等的恒力F1、F2作用下静止在相同的竖直墙面上.则( )
如图所示,a、b是截面为等腰直角三角形的两个相同的楔形物体,分别在垂直于斜边的大小相等的恒力F1、F2作用下静止在相同的竖直墙面上.则( )
 如图所示,a、b是截面为等腰直角三角形的两个相同的楔形物体,分别在垂直于斜边的大小相等的恒力F1、F2作用下静止在相同的竖直墙面上.则( )
如图所示,a、b是截面为等腰直角三角形的两个相同的楔形物体,分别在垂直于斜边的大小相等的恒力F1、F2作用下静止在相同的竖直墙面上.则( )| A. | a受到摩擦力可能为零 | B. | b受到摩擦力可能为零 | ||
| C. | 墙面对a的弹力大于墙面对b的弹力 | D. | 墙面对a的弹力小于墙面对b的弹力 |
 如图所示,光滑水平直轨道上有三个滑块A、B、C,质量分别为mA=mC=2kg,mB=1kg,A、B用细绳连接,中间有一压缩的轻弹簧(弹簧与滑块不栓接).开始时A、B以初速度v0=10m/s运动,C静止.某时刻细绳突然断开,A、B被弹开,然后B又与C发生碰撞并粘在一起,最终三滑块速度恰好相同.求:
如图所示,光滑水平直轨道上有三个滑块A、B、C,质量分别为mA=mC=2kg,mB=1kg,A、B用细绳连接,中间有一压缩的轻弹簧(弹簧与滑块不栓接).开始时A、B以初速度v0=10m/s运动,C静止.某时刻细绳突然断开,A、B被弹开,然后B又与C发生碰撞并粘在一起,最终三滑块速度恰好相同.求:

 如图所示,足够长的水平传送带以速度v1=3m/s向左运动,t=0时刻质量m=5kg的物体P以v2=9m/s的初速度沿传动带的最左端开始往右运动,物体P与传动带间的动摩擦因数μ=0.5,拉力F=50N通过定滑轮且不可伸长的轻绳与物体P相连,设最低静摩擦力等于滑动摩擦力,P与定滑轮间的绳水平,不计定滑轮质量和摩擦,绳足够长.
如图所示,足够长的水平传送带以速度v1=3m/s向左运动,t=0时刻质量m=5kg的物体P以v2=9m/s的初速度沿传动带的最左端开始往右运动,物体P与传动带间的动摩擦因数μ=0.5,拉力F=50N通过定滑轮且不可伸长的轻绳与物体P相连,设最低静摩擦力等于滑动摩擦力,P与定滑轮间的绳水平,不计定滑轮质量和摩擦,绳足够长.