题目内容
2. 如图所示为一绕地球运行的人造地球卫星运行轨迹,卫星近地点P近似认为贴近地球表面,远地点Q距地面的高度为h,已知地球半径为R,地球表面重力加速度为g,则( )
如图所示为一绕地球运行的人造地球卫星运行轨迹,卫星近地点P近似认为贴近地球表面,远地点Q距地面的高度为h,已知地球半径为R,地球表面重力加速度为g,则( )| A. | 该卫星的运动周期为2π$\sqrt{\frac{(R+\frac{h}{2})^{2}}{g{R}^{2}}}$ | |
| B. | 该卫星的发射速度大于第一宇宙速度 | |
| C. | 该卫星在P点的速度大小为$\sqrt{gR}$ | |
| D. | 该卫星在P点的加速度大于地球表面的重力加速度g |
分析 求出卫星椭圆轨道的半长轴,抓住椭圆的周期与圆轨道半径等于半长轴的周期相等,结合万有引力提供向心力求出周期.在P点,卫星的速度大于第一宇宙速度,做离心运动.根据牛顿第二定律,结合万有引力等于重力比较卫星在P点的加速度与地球表面重力加速度的大小关系.
解答 解:A、近地卫星的周期为${T}_{0}^{\;}$,由$mg=m\frac{4{π}_{\;}^{2}}{{T}_{0}^{2}}R$,得${T}_{0}^{\;}=2π\sqrt{\frac{{R}_{\;}^{3}}{GM}}$=$2π\sqrt{\frac{{R}_{\;}^{3}}{g{R}_{\;}^{2}}}=2π\sqrt{\frac{R}{g}}$,图示卫星的周期为T,半长轴为$r=(R+\frac{h}{2})$,由开普勒第三定律得$\frac{{R}_{\;}^{3}}{{T}_{0}^{2}}=\frac{{r}_{\;}^{3}}{{T}_{\;}^{2}}$,解得$T=2π\sqrt{\frac{(g+\frac{h}{2})_{\;}^{3}}{g{R}_{\;}^{2}}}$,故A正确;
C、因卫星的轨道为椭圆,故卫星的发射速度大于$\sqrt{gR}$,故C错误;
B、发射速度大于第一宇宙速度,故B正确;
D、由万有引力定律和牛顿第二定律知卫星在P点的加速度在P点,加速度a=$\frac{G\frac{Mm}{{R}_{\;}^{2}}}{m}=\frac{GM}{{R}_{\;}^{2}}$,地球表面的重力加速度g=$\frac{GM}{{R}_{\;}^{2}}$,即P点加速度等于地球表面的重力加速度,故D错误;
故选:AB
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,运用开普勒第三定律必须对于同一个中心天体.

| A. | 库仑用扭秤测出了万有引力常量 | |
| B. | 牛顿通过理想斜面实验发现了物体的运动不需要力来维持 | |
| C. | 法拉第通过实验发现了电磁感应现象 | |
| D. | 奥斯特通过实验发现了电流的热效应 |
| A. | 15 m/s2 | B. | 20 m/s2 | C. | 25 m/s2 | D. | 0m/s2 |
 如图所示,弹簧的一端固定在竖直墙上,质量为M 的光滑弧形槽静止在光滑水平面上,底部与水平面平滑连接,一个质量为m(m<M)的小球从槽高h 处开始自由下滑,下列说法正确的是( )
如图所示,弹簧的一端固定在竖直墙上,质量为M 的光滑弧形槽静止在光滑水平面上,底部与水平面平滑连接,一个质量为m(m<M)的小球从槽高h 处开始自由下滑,下列说法正确的是( )| A. | 在以后的运动过程中,小球和槽的水平方向动量始终守恒 | |
| B. | 被弹簧反弹后,小球和槽的机械能守恒,但小球不能回到槽高h处 | |
| C. | 全过程小球和槽、弹簧所组成的系统机械能守恒,且水平方向动量守恒 | |
| D. | 在下滑过程中小球和槽之间的相互作用力始终不做功? |
 木块 A、B 分别重 50N 和 30N,它们与水平地面之间的动摩擦因数均为 0.2.与 A、B 相连接的轻弹簧被压缩了 5cm,系统置于水平地面上静止不动.已知弹 簧的劲度系数为 100N/m.用 F=1N 的水平力作用在木块 A 上,如图所示,力 F 作用后( )
木块 A、B 分别重 50N 和 30N,它们与水平地面之间的动摩擦因数均为 0.2.与 A、B 相连接的轻弹簧被压缩了 5cm,系统置于水平地面上静止不动.已知弹 簧的劲度系数为 100N/m.用 F=1N 的水平力作用在木块 A 上,如图所示,力 F 作用后( )| A. | 木块 A 所受摩擦力大小是 4 N,方向向右 | |
| B. | 木块 A 所受摩擦力大小是 5 N,方向向右 | |
| C. | 木块 B 所受摩擦力大小是 4 N,方向向左 | |
| D. | 木块 B 所受摩擦力大小是 5 N,方向向左 |

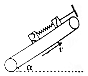 如图所示,倾角为α的传送带上有质量均为m的两个木块1、2,它们之间用原长为L、劲度系数为k的轻弹簧连接起来,木块与传送带间的动摩擦因数均为μ,其中木块1被与传送带平行的细线拉住,传动带按图示方向匀速运动,两个木块均处于平衡状态.求:
如图所示,倾角为α的传送带上有质量均为m的两个木块1、2,它们之间用原长为L、劲度系数为k的轻弹簧连接起来,木块与传送带间的动摩擦因数均为μ,其中木块1被与传送带平行的细线拉住,传动带按图示方向匀速运动,两个木块均处于平衡状态.求: