题目内容
15. 如图所示,斜面固定于水平面上,物体A置于光滑斜面上,斜面倾角α=30°,小滑轮1的上端正好与悬点O相平且相距为2d,两光滑滑轮通过细绳连接着A、B两物体,质量分别为M和m;刚开始时两物体均处于静止状态,夹角β=120°.然后用力F将物体B向下缓慢拉一小段距离,使夹角β变为60°时撤去拉力F,下拉过程中,物体A始终没有接触斜面上的滑轮,下滑过程中物体A也没有滑到水平面上,则从撤掉拉力到物体A运动到最低点的过程中,下列说法正确的是( )
如图所示,斜面固定于水平面上,物体A置于光滑斜面上,斜面倾角α=30°,小滑轮1的上端正好与悬点O相平且相距为2d,两光滑滑轮通过细绳连接着A、B两物体,质量分别为M和m;刚开始时两物体均处于静止状态,夹角β=120°.然后用力F将物体B向下缓慢拉一小段距离,使夹角β变为60°时撤去拉力F,下拉过程中,物体A始终没有接触斜面上的滑轮,下滑过程中物体A也没有滑到水平面上,则从撤掉拉力到物体A运动到最低点的过程中,下列说法正确的是( )| A. | 质量关系M=2m,撤掉力F后绳子的拉力越来越大 | |
| B. | 刚撤掉拉力的瞬间物体B的加速度大小是($\sqrt{3}$-1)g | |
| C. | B向上运动的过程中,滑轮1左侧的绳子一定能伸直 | |
| D. | 物体B向上运动的最大速度大小为vm=$\sqrt{\frac{4(2-\sqrt{3})}{3}gd}$ |
分析 根据刚开始时两物体均处于静止状态,由平衡条件求解M与m的关系.分析刚撤掉拉力的瞬间物体B的合力,由牛顿第二定律求解其加速度.当B的合力为零时速度最大,由系统的机械能守恒和几何关系结合求解最大速度.
解答 解:AC、刚开始时两物体均处于静止状态,则有:
2Tcos60°=mg,
T=Mgsin30°,
得 M=2m
设B向上运动的过程中上升的最大高度为h,根据两个物体组成的系统机械能守恒得:
mgh=Mgsinα•($\frac{d}{sin30°}$-$\sqrt{{d}^{2}+(dcot30°-h)^{2}}$)
解得:h=2$\sqrt{3}$d>dvot30°,所以B向上运动的过程中,滑轮1左侧的绳子一定能伸直,绳子的拉力先越来越大,当滑轮1左侧的绳子伸直后拉力越来越小.故A错误,C正确.
B、刚撤掉拉力前的瞬间F的大小为:
F=2Mgcos30°-mg=(2$\sqrt{3}$-1)mg
刚撤掉拉力的瞬间物体B的合力大小等于F,则刚撤掉拉力的瞬间物体B的加速度大小是:
a=$\frac{F}{m}$=(2$\sqrt{3}$-1)g.故B错误.
C、D、当β=120°时,物体B向上运动的速度最大,由系统的机械能守恒得:
Mg($\frac{d}{sin30°}$-$\frac{d}{sin60°}$)=mg(dcot30°-dcot60°)+$\frac{1}{2}m{v}_{m}^{2}$+$\frac{1}{2}M{v}_{A}^{2}$
又 由速度的分解可知:vA=vmcos60°
联立解得:vm=$\sqrt{\frac{4(2-\sqrt{3})}{3}gd}$.故D正确.
故选:CD.
点评 本题是共点力平衡、牛顿第二定律和机械能守恒定律的综合,关键要正确分析物体的受力情况,明确系统的机械能是守恒的.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案 如图所示,水平地面上有一坑,其竖直截面为半圆,ab为沿水平方向的直径,O为球心,若在a点以某一初速度沿ab方向抛出一小球,小球击中坑壁,不计空气阻力,则( )
如图所示,水平地面上有一坑,其竖直截面为半圆,ab为沿水平方向的直径,O为球心,若在a点以某一初速度沿ab方向抛出一小球,小球击中坑壁,不计空气阻力,则( )| A. | 小球的初速度越大,在坑中运动的时间一定越长 | |
| B. | 小球的初速度不同,在坑中的运动时间可能相同 | |
| C. | 小球与坑壁相撞时速度方向的反向延长线可能过O点 | |
| D. | 小球与坑壁相撞时速度方向的反向延长线不可能过O点 |
 如图所示,实现为沿x轴传播的一列简谐横波在t=0时刻的波形图,质点P恰好在平衡位置,虚线是这列波在t=0.2s时刻的波形图.已知该波的波速是0.8m/s,那么,则下列说法中正确的是( )
如图所示,实现为沿x轴传播的一列简谐横波在t=0时刻的波形图,质点P恰好在平衡位置,虚线是这列波在t=0.2s时刻的波形图.已知该波的波速是0.8m/s,那么,则下列说法中正确的是( )| A. | 这列波可能是沿x轴正方向传播的 | |
| B. | 在t=0时,x=4cm处的质点P的速度沿y轴负方向 | |
| C. | 质点P在0.6s时间内经过的路程为0.48m | |
| D. | 质点P在t=0.31s时刻速度方向与加速度方向相同 |
| A. | 同一次实验过程中,O点位置允许变动 | |
| B. | 实验中,弹簧秤必须保持与木板平行,读数时视线要正对弹簧秤刻度 | |
| C. | 实验中,把橡皮条的另一端拉到O点时,两个弹簧秤之间夹角应取90°,以方便计算合力 | |
| D. | 实验中两绳套应该长一些,以便方便确定弹簧秤拉力的方向,但它们的必须长度相同 | |
| E. | 实验时,量弹簧秤拉力的方向的夹角尽量大些,记录拉力方向时铅笔应尽量细些,以便记录拉力方向,减少作图带来的相对误差 |
 如图所示,V1、V2是理想电压表,当闭合开关,将滑动变阻器的触片由左端向右滑动时,下列说法中正确的是( )
如图所示,V1、V2是理想电压表,当闭合开关,将滑动变阻器的触片由左端向右滑动时,下列说法中正确的是( )| A. | 小灯泡L2变暗,V1表的读数变小,V2表的读数变大 | |
| B. | 小灯泡L1变亮,V1表的读数变大,V2表的读数变小 | |
| C. | 小灯泡L2变亮,V1表的读数变大,V2表的读数变小 | |
| D. | 小灯泡L1变暗,V1表的读数变小,V2表的读数变大 |

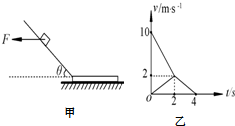 如图甲所示,有一倾角为30°的光滑固定斜面,斜面底端的水平面上放一质量为M的木板.开始时质量为m=1kg的滑块在水平向左的力F作用下静止在斜面上,今将水平力F变为水平向右,当滑块滑到木板上时撤去力F,滑块滑上木板的过程不考虑能量损失.此后滑块和木板在水平上运动的v-t图象如图乙所示,g=10m/s2.求
如图甲所示,有一倾角为30°的光滑固定斜面,斜面底端的水平面上放一质量为M的木板.开始时质量为m=1kg的滑块在水平向左的力F作用下静止在斜面上,今将水平力F变为水平向右,当滑块滑到木板上时撤去力F,滑块滑上木板的过程不考虑能量损失.此后滑块和木板在水平上运动的v-t图象如图乙所示,g=10m/s2.求 一列简谐横波以5m/s的速度沿x轴正方向传播,在t=0时刻,波恰好传到x=4m处,波形如图所示,则波源起振方向沿y轴正方向(填“正”或“负”),质点P的坐标为(18,0),t=3s时,质点P第一次到达波峰.
一列简谐横波以5m/s的速度沿x轴正方向传播,在t=0时刻,波恰好传到x=4m处,波形如图所示,则波源起振方向沿y轴正方向(填“正”或“负”),质点P的坐标为(18,0),t=3s时,质点P第一次到达波峰.