题目内容
10. 如图所示,粗糙水平地面与半径为R=0.4m的光滑半圆轨道BCD相连接,且在同一竖直平面内,O是BCD的圆心,BOD在同一竖直线上,质量为m的小物块在水平拉力F的作用下,由静止开始从A点开始做加速直线运动,当小物块运动到B点时撤去F,小物块沿半圆轨道运动恰好能通过D点,重力加速度g=10m/s2,求:
如图所示,粗糙水平地面与半径为R=0.4m的光滑半圆轨道BCD相连接,且在同一竖直平面内,O是BCD的圆心,BOD在同一竖直线上,质量为m的小物块在水平拉力F的作用下,由静止开始从A点开始做加速直线运动,当小物块运动到B点时撤去F,小物块沿半圆轨道运动恰好能通过D点,重力加速度g=10m/s2,求:(1)小物块离开D点后落到地面上的点与B点之间的距离;
(2)小物块经过B点时的速度.
分析 (1)对物块进行受力分析,小物块恰好能通过D点,所以在D点小物块所受重力等于向心力,根据牛顿第二定律求解D点的速度,设小物块落地点距B点之间的距离为x,下落时间为t,根据平抛运动的规律即可求解;
(2)物块由B点运动到D点的过程中机械能守恒,根据机械能守恒定律列式即可求解;
解答 解:(1)设小物块离开D点时速度为vD,则有:
$mg=m\frac{{{v_D}^2}}{R}$
代入数据解得:vD=2m/s
且$t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×0.8}{10}}=0.4s$
则小物块落点与B点间的距离为:
x=vDt=2×0.4=0.8m
(2)设小物块经过B点时的速度为vB,则有:
$\frac{1}{2}m{v_B}^2=\frac{1}{2}m{v_D}^2+mg2R$
解得:${v_B}=\sqrt{{v_D}^2+4gR}=\sqrt{{2^2}+4×10×0.4}=2\sqrt{5}m/s$
答:(1)小物块离开D点后落到地面上的点与B点之间的距离是0.8m;
(2)小物块经过B点时的速度是$2\sqrt{5}$m/s.
点评 本题是机械能守恒定律、牛顿第二定律和平抛运动规律的综合应用,关键是确定运动过程,分析运动规律.

练习册系列答案
相关题目
20. 长为L的长木板水平放置,在木板的A端放置一个质量为m的小物块(可视为质点),现缓慢地抬高A端,使木板以左端为轴转动,当木板转到与水平面的夹角为α时小物块开始滑动(如图所示),此时停止转动木板,小物块滑到底端的速度为v,则对整个过程,下列说法不正确的是( )
长为L的长木板水平放置,在木板的A端放置一个质量为m的小物块(可视为质点),现缓慢地抬高A端,使木板以左端为轴转动,当木板转到与水平面的夹角为α时小物块开始滑动(如图所示),此时停止转动木板,小物块滑到底端的速度为v,则对整个过程,下列说法不正确的是( )
 长为L的长木板水平放置,在木板的A端放置一个质量为m的小物块(可视为质点),现缓慢地抬高A端,使木板以左端为轴转动,当木板转到与水平面的夹角为α时小物块开始滑动(如图所示),此时停止转动木板,小物块滑到底端的速度为v,则对整个过程,下列说法不正确的是( )
长为L的长木板水平放置,在木板的A端放置一个质量为m的小物块(可视为质点),现缓慢地抬高A端,使木板以左端为轴转动,当木板转到与水平面的夹角为α时小物块开始滑动(如图所示),此时停止转动木板,小物块滑到底端的速度为v,则对整个过程,下列说法不正确的是( )| A. | 木板对物块的力所做的总功为$\frac{1}{2}$mv2 | |
| B. | 木板对小物块的摩擦力所做的功为mgLsinα | |
| C. | 木板对小物块的支持力所做的功为mgLsinα | |
| D. | 木块对小物块的滑动摩擦力所做的功为$\frac{1}{2}$mv2-mgLsinα |
1. 如图所示,一个卫星围绕某行星做匀速圆周运动,此行星的质量和半径分别是地球质量M和半径R的a倍和b倍,万有引力常量为G,则下列说法正确的是( )
如图所示,一个卫星围绕某行星做匀速圆周运动,此行星的质量和半径分别是地球质量M和半径R的a倍和b倍,万有引力常量为G,则下列说法正确的是( )
 如图所示,一个卫星围绕某行星做匀速圆周运动,此行星的质量和半径分别是地球质量M和半径R的a倍和b倍,万有引力常量为G,则下列说法正确的是( )
如图所示,一个卫星围绕某行星做匀速圆周运动,此行星的质量和半径分别是地球质量M和半径R的a倍和b倍,万有引力常量为G,则下列说法正确的是( )| A. | 卫星在轨道上运动的速度大于第一宇宙速度 | |
| B. | 此行星的第一宇宙的速度是地球第一宇宙的$\sqrt{\frac{a}{b}}$倍 | |
| C. | 卫星轨道上运动时,如果速度减小,卫星将到达高轨道运动 | |
| D. | 如果卫星公转周期等于行星的自转周期,则卫星是该行星的同步卫星 |
5.某物体运动的v-t图象如图所示,则下列说法正确的是( )


| A. | 物体在第1s末运动方向发生改变 | |
| B. | 物体在第2s内、第3s内的加速度是相同的 | |
| C. | 物体在第2s末离出发点最远,且最大位移为1m | |
| D. | 物体在第5s时离出发点最远,且最大位移为0.5m |
15. 如图所示,小球在竖直向下的力F作用下,将竖直轻弹簧压缩,若将力F撤去,小球将向上弹起并离开弹簧直到速度为零.在小球向上运动的整个过程中,下列说法正确的是( )
如图所示,小球在竖直向下的力F作用下,将竖直轻弹簧压缩,若将力F撤去,小球将向上弹起并离开弹簧直到速度为零.在小球向上运动的整个过程中,下列说法正确的是( )
 如图所示,小球在竖直向下的力F作用下,将竖直轻弹簧压缩,若将力F撤去,小球将向上弹起并离开弹簧直到速度为零.在小球向上运动的整个过程中,下列说法正确的是( )
如图所示,小球在竖直向下的力F作用下,将竖直轻弹簧压缩,若将力F撤去,小球将向上弹起并离开弹簧直到速度为零.在小球向上运动的整个过程中,下列说法正确的是( )| A. | 小球的动能先增大后减小 | |
| B. | 小球的机械能守恒,小球和弹簧组成的系统机械能不守恒 | |
| C. | 小球离开弹簧时动能最大 | |
| D. | 小球动能最大时弹性势能不为零 |
2.某实验小组采用如图甲所示的装置探究功与速度变化的关系.
(1)在一次实验中得到了一条如图乙所示的纸带,图中数据为相邻两点的距离,下列说法正确的是BDE
A.纸带的左端是与小车相连的
B.纸带的右端是与小车相连的
C.利用C、D、E、F这些点之间的距离来确定小车的速度
D.利用A、B、C、D这些点之间的距离来确定小车的速度
E.实验中木板略微倾斜,这样做的目的是可使得橡皮筋做的功等于合外力对小车做的功
(2)下面是本实验的数据记录表:
为进一步直观反映功与速度变化的关系,请根据如表数据,选择恰当的物理量在图丙所示的坐标系中作出相应的图象.
由图象得出的结论在误差范围允许内,橡皮筋对小车做的功等于小车动能的改变量.
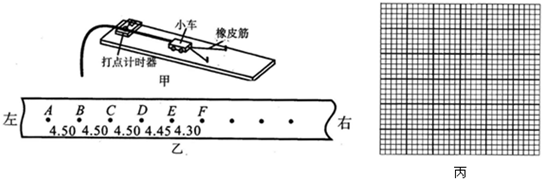
(1)在一次实验中得到了一条如图乙所示的纸带,图中数据为相邻两点的距离,下列说法正确的是BDE
A.纸带的左端是与小车相连的
B.纸带的右端是与小车相连的
C.利用C、D、E、F这些点之间的距离来确定小车的速度
D.利用A、B、C、D这些点之间的距离来确定小车的速度
E.实验中木板略微倾斜,这样做的目的是可使得橡皮筋做的功等于合外力对小车做的功
(2)下面是本实验的数据记录表:
| 数据 项目 次数 | 橡皮筋做的功 | 10个均匀间隔的距离xn(m) | 10个间隔的时间t(s) | 小车获得的速度vn(m/s) | 小车速度的平方vn2(m2/s2) |
| 1 | W | 0.288 | 0.2 | 1.44 | 2.07 |
| 2 | 2W | 0.417 | 0.2 | 2.09 | 4.37 |
| 3 | 3W | 0.489 | 0.2 | 2.45 | 6.00 |
| 4 | 4W | 0.590 | 0.2 | 2.95 | 8.70 |
| 5 | 5W | 0.648 | 0.2 | 3.24 | 10.50 |
由图象得出的结论在误差范围允许内,橡皮筋对小车做的功等于小车动能的改变量.

19.关于电磁波,下列说法中正确的是( )
| A. | 电磁波中最容易表现出衍射现象的是无线电波 | |
| B. | 紫外线可使钞票上的荧光物质发光 | |
| C. | 电磁波的传播不需要介质,机械波的传播需要介质 | |
| D. | 红外线的显著作用是热效应,温度较低的物体不能辐射红外线 |
20.地球半径为R,地面重力加速度为g,地球自转周期为T,地球同步卫星离地面的高度为h,则地球同步卫星的线速度大小为( )
| A. | $\sqrt{(R+h)g}$ | B. | $\sqrt{\frac{{R}^{2}g}{R+h}}$ | C. | $\frac{2π(R+h)}{T}$ | D. | $\frac{2πR}{T}$ |