题目内容
20.地球半径为R,地面重力加速度为g,地球自转周期为T,地球同步卫星离地面的高度为h,则地球同步卫星的线速度大小为( )| A. | $\sqrt{(R+h)g}$ | B. | $\sqrt{\frac{{R}^{2}g}{R+h}}$ | C. | $\frac{2π(R+h)}{T}$ | D. | $\frac{2πR}{T}$ |
分析 万有引力提供向心力,应用牛顿第二定律可以求出线速度;已知周期与轨道半径,应用线速度与周期的关系可以求出线速度.
解答 解:A地球同步卫星绕地球做圆周运动,万有引力提供向心力,由牛顿第二定律得:G$\frac{Mm}{(R+h)^{2}}$=m$\frac{{v}^{2}}{R+h}$,在地球表面:m′g=G $\frac{Mm}{{R}^{2}}$,解得:v=$\sqrt{\frac{g{R}^{2}}{R+h}}$,故A错误,B正确;
C、由于地球同步卫星的运动周期等于地球自转的周期,故地球同步卫星的运动周期等于T,地球同步卫星的线速度大小为:v=ωr=$\frac{2π}{T}$×(R+h)=$\frac{2π(R+h)}{T}$,故C正确,D错误;
故选:BC.
点评 本题考查了万有引力提供向心力公式,黄金代换公式,同步卫星的特点和线速度的定义式,是一道不可多得的好题.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
11.两个分别带有电荷量-Q和+4Q的相同金属小球(均可视为点电荷),固定在相距为r的两处,它们间库仑力的大小为F,两小球相互接触后将其固定距离变为$\frac{1}{2}$r,则两球间库仑力的大小为( )
| A. | 12F | B. | 9F | C. | $\frac{9}{4}$F | D. | F |
8.下列说法中正确的是( )
| A. | 氢原子从激发态向基态跃迁只能辐射特定频率的光子 | |
| B. | 原子核所含核子单独存在时的总质量小于该原子核的质量 | |
| C. | 一个动量为p的电子对应的物质波波长为hp(h为普朗克常量) | |
| D. | 在研究光电效应实验中所测得的遏制电压与入射光的强度有关 |
15.一轻杆一端固定一质量为m的小球,以另一端O为圆心,使小球在竖直平面内做半径为R的圆周运动,以下说法正确的( )
| A. | 小球过最高点时,杆所受的弹力不可以为零 | |
| B. | 小球过最高点时最小速度为$\sqrt{gR}$ | |
| C. | 小球过最高点时,杆对球的作用力一定与小球所受重力方向相同 | |
| D. | 小球过最高点时,杆对球的作用力方向可以与小球所受重力方向相反 |
9.如图所示的金属圆环放在有界匀强磁场中,将它从磁场中匀速拉出的过程中,下列说法正确的是( )
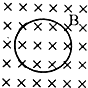

| A. | 向左拉出和向右拉出,其感应电流方向相反 | |
| B. | 不管从什么方向拉出,环中的感应电流总是逆时针方向 | |
| C. | 不管从什么方向拉出,环中的感应电流总是顺时针方向 | |
| D. | 在匀速拉出过程中感应电流大小不变 |
10.下列关于物理学史的说法正确的是( )
| A. | 汤姆孙利用气体放电管研究阴极射线时发现了电子 | |
| B. | 查德威克利用a粒子轰击氮原子核发现了质子 | |
| C. | 玻尔的原子理论成功地解释了光电效应的实验规律 | |
| D. | 爱因斯坦的光电效应方程成功地解释了氢原子光谱的实验规律 |
 如图所示,粗糙水平地面与半径为R=0.4m的光滑半圆轨道BCD相连接,且在同一竖直平面内,O是BCD的圆心,BOD在同一竖直线上,质量为m的小物块在水平拉力F的作用下,由静止开始从A点开始做加速直线运动,当小物块运动到B点时撤去F,小物块沿半圆轨道运动恰好能通过D点,重力加速度g=10m/s2,求:
如图所示,粗糙水平地面与半径为R=0.4m的光滑半圆轨道BCD相连接,且在同一竖直平面内,O是BCD的圆心,BOD在同一竖直线上,质量为m的小物块在水平拉力F的作用下,由静止开始从A点开始做加速直线运动,当小物块运动到B点时撤去F,小物块沿半圆轨道运动恰好能通过D点,重力加速度g=10m/s2,求:
 A、B两个小球半径相同,质量不同,并排悬挂在同样长度的绳子上,彼此相互接触,把质量为m0的A球拉开后由静止释放,当A球与B球相碰前其速度为v0,碰撞后量小球的动量相等,则:
A、B两个小球半径相同,质量不同,并排悬挂在同样长度的绳子上,彼此相互接触,把质量为m0的A球拉开后由静止释放,当A球与B球相碰前其速度为v0,碰撞后量小球的动量相等,则: