题目内容
11. 如图所示,水平传送带AB的长L=18m,传送带以v0=2m/s的速度匀速转动,现将一质量m=2.5kg的小物块(可视为质点)无初速度地放于传送带的A点,最后从B处离开传送带,物块与传送带间的动摩擦因数μ=0.4,取重力加速度昏g=10m/s2.物块由A到B的过程中,求:
如图所示,水平传送带AB的长L=18m,传送带以v0=2m/s的速度匀速转动,现将一质量m=2.5kg的小物块(可视为质点)无初速度地放于传送带的A点,最后从B处离开传送带,物块与传送带间的动摩擦因数μ=0.4,取重力加速度昏g=10m/s2.物块由A到B的过程中,求:(1)摩擦力对物块做的功Wf;
(2)传送带克服摩擦力做的功Wf′以及系统内摩擦力做的总功W.
分析 (1)根据牛顿第二定律求出物块刚开始运动时的加速度.根据匀变速直线运动速度时间公式求出求出小物块加速运动的时间,结合位移公式求出加速运动的位移,从而求出摩擦力做的功;
(2)求出传送带的位移,从而求出传送带克服摩擦力做的功,摩擦力对滑块和对传送带做功的代数和即系统内摩擦力做的总功.
解答 解:(1)对物块刚开始运动时,根据牛顿第二定律,有:μmg=ma,
解得:$a=μg=4m/{s}_{\;}^{2}$
匀加速运动的时间为:$t=\frac{{v}_{0}^{\;}}{a}=\frac{2}{4}=0.5s$
匀加速运动的位移为:$x=\frac{1}{2}a{t}_{\;}^{2}=\frac{1}{2}×4×0.{5}_{\;}^{2}=0.5m$
摩擦力对物块所做的功为:${W}_{f}^{\;}=fx=μmgx=5J$
(2)传送带位移为:$x′={v}_{0}^{\;}t=2×0.5=1m$
传送带克服摩擦力做的功为:${W}_{f}^{′}=fx′=μmgx′=10J$
系统内摩擦力做的总功为:$W=-{W}_{f}^{′}+{W}_{f}^{\;}=-10+5=-5J$
答:(1)摩擦力对物块做的功${W}_{f}^{\;}$为5J;
(2)传送带克服摩擦力做的功${W}_{f}^{′}$为10J以及系统内摩擦力做的总功W为-5J.
点评 解决本题的关键理清煤块在传送带上的运动规律,结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
7. 如图所示,物体A的质量是B的2倍,中间有一压缩的弹簧,放在光滑水平面上,由静止同时放开两手后的一小段时间后,下列结论正确的是( )
如图所示,物体A的质量是B的2倍,中间有一压缩的弹簧,放在光滑水平面上,由静止同时放开两手后的一小段时间后,下列结论正确的是( )
 如图所示,物体A的质量是B的2倍,中间有一压缩的弹簧,放在光滑水平面上,由静止同时放开两手后的一小段时间后,下列结论正确的是( )
如图所示,物体A的质量是B的2倍,中间有一压缩的弹簧,放在光滑水平面上,由静止同时放开两手后的一小段时间后,下列结论正确的是( )| A. | A的速率是B的一半 | B. | A的动量和B的动量相同 | ||
| C. | A受的力大于B受的力 | D. | A和B的总动量为零 |
2. 如图,甲、乙两颗卫星以相同的轨道半径分别绕质量为M和2M的行星做匀速圆周运动,且甲、乙的质量分别为2m、m,下列说法正确的是 ( )
如图,甲、乙两颗卫星以相同的轨道半径分别绕质量为M和2M的行星做匀速圆周运动,且甲、乙的质量分别为2m、m,下列说法正确的是 ( )
 如图,甲、乙两颗卫星以相同的轨道半径分别绕质量为M和2M的行星做匀速圆周运动,且甲、乙的质量分别为2m、m,下列说法正确的是 ( )
如图,甲、乙两颗卫星以相同的轨道半径分别绕质量为M和2M的行星做匀速圆周运动,且甲、乙的质量分别为2m、m,下列说法正确的是 ( )| A. | 甲的向心力比乙的小 | B. | 两卫星的向心加速度大小相等 | ||
| C. | 甲的运行周期比乙的大 | D. | 甲的角速度比乙的大 |
16.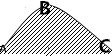 用弹射器从A点竖直向上弹出一质量为m的小球,因受水平方向恒定风力的作用,轨迹如图所示,B、C为小球运动经过的两点,B为轨迹的最高点,C点与A点等高,小球在A、B两点时的速率均为v,不计空气阻力,则( )
用弹射器从A点竖直向上弹出一质量为m的小球,因受水平方向恒定风力的作用,轨迹如图所示,B、C为小球运动经过的两点,B为轨迹的最高点,C点与A点等高,小球在A、B两点时的速率均为v,不计空气阻力,则( )
 用弹射器从A点竖直向上弹出一质量为m的小球,因受水平方向恒定风力的作用,轨迹如图所示,B、C为小球运动经过的两点,B为轨迹的最高点,C点与A点等高,小球在A、B两点时的速率均为v,不计空气阻力,则( )
用弹射器从A点竖直向上弹出一质量为m的小球,因受水平方向恒定风力的作用,轨迹如图所示,B、C为小球运动经过的两点,B为轨迹的最高点,C点与A点等高,小球在A、B两点时的速率均为v,不计空气阻力,则( )| A. | 小球受水平风力的大小为2mg | |
| B. | AB的水平距离与BC的水平距离之比为1:3 | |
| C. | 小球从A到C的过程中最小动能为$\frac{1}{4}$mv2 | |
| D. | 小球从A到C的过程中机械能增加为$\frac{3}{2}$mv2 |
3.李明在教学楼顶用玩具手枪向楼前广场水平射出一颗子弹,若不计空气阻力,则( )
| A. | 子弹在空中做变加速曲线运动 | |
| B. | 子弹在空中运动时间与子弹发射速度成正比 | |
| C. | 子弹落地时的速度方向仍是水平向前 | |
| D. | 子弹落地点距发射点的水平距离与教学楼高度有关 |
20.下列几种情况中,甲、乙两物体的动能相等的是( )
| A. | 甲的速度是乙的2倍,乙的质量是甲的2倍 | |
| B. | 甲的质量是乙的2倍,乙的速度是甲的2倍 | |
| C. | 甲的质量是乙的4倍,乙的速度是甲的2倍 | |
| D. | 以上说法都不对 |
1. “太极球”是近年来在广大市民中较流行的一种健身器材.做该项运动时,健身者半马步站立,手持太极球拍,拍上放一橡胶太极球,健身者舞动球拍时,球却不会掉落地上.现将太极球简化成如图所示的平板和小球,熟练的健身者让球在竖直面内始终不脱离板而做匀速圆周运动,且在运动到图中的A、B、C、D位置时球与板间无相对运动趋势.A为圆周的最高点,C为最低点,B、D与圆心O等高且在B、D处板与水平面夹角为θ.设球的质量为m,圆周的半径为R,重力加速度为g,不计拍的重力,若运动过程到最高点时拍与小球之间作用力恰为mg,则( )
“太极球”是近年来在广大市民中较流行的一种健身器材.做该项运动时,健身者半马步站立,手持太极球拍,拍上放一橡胶太极球,健身者舞动球拍时,球却不会掉落地上.现将太极球简化成如图所示的平板和小球,熟练的健身者让球在竖直面内始终不脱离板而做匀速圆周运动,且在运动到图中的A、B、C、D位置时球与板间无相对运动趋势.A为圆周的最高点,C为最低点,B、D与圆心O等高且在B、D处板与水平面夹角为θ.设球的质量为m,圆周的半径为R,重力加速度为g,不计拍的重力,若运动过程到最高点时拍与小球之间作用力恰为mg,则( )
 “太极球”是近年来在广大市民中较流行的一种健身器材.做该项运动时,健身者半马步站立,手持太极球拍,拍上放一橡胶太极球,健身者舞动球拍时,球却不会掉落地上.现将太极球简化成如图所示的平板和小球,熟练的健身者让球在竖直面内始终不脱离板而做匀速圆周运动,且在运动到图中的A、B、C、D位置时球与板间无相对运动趋势.A为圆周的最高点,C为最低点,B、D与圆心O等高且在B、D处板与水平面夹角为θ.设球的质量为m,圆周的半径为R,重力加速度为g,不计拍的重力,若运动过程到最高点时拍与小球之间作用力恰为mg,则( )
“太极球”是近年来在广大市民中较流行的一种健身器材.做该项运动时,健身者半马步站立,手持太极球拍,拍上放一橡胶太极球,健身者舞动球拍时,球却不会掉落地上.现将太极球简化成如图所示的平板和小球,熟练的健身者让球在竖直面内始终不脱离板而做匀速圆周运动,且在运动到图中的A、B、C、D位置时球与板间无相对运动趋势.A为圆周的最高点,C为最低点,B、D与圆心O等高且在B、D处板与水平面夹角为θ.设球的质量为m,圆周的半径为R,重力加速度为g,不计拍的重力,若运动过程到最高点时拍与小球之间作用力恰为mg,则( )| A. | 圆周运动的周期为:T=π$\sqrt{\frac{2R}{g}}$ | |
| B. | 圆周运动的周期为:T=2π$\sqrt{\frac{R}{g}}$ | |
| C. | 在B、D处球拍对球的作用力为$\frac{2mg}{sinθ}$ | |
| D. | 在B、D处球拍对球的作用力为5mg |
 如图所示的物体静止在水平桌面上,当用F1=25N的力水平向右拉物体时,物体静止不动,这时物体所受到的摩擦力大小为25N,方向向左;当用F2=50N的水平力向右拉物体时,物体恰能开始滑动,则物体所受到的最大静摩擦力大小为50N.
如图所示的物体静止在水平桌面上,当用F1=25N的力水平向右拉物体时,物体静止不动,这时物体所受到的摩擦力大小为25N,方向向左;当用F2=50N的水平力向右拉物体时,物体恰能开始滑动,则物体所受到的最大静摩擦力大小为50N. 在质量为0.5kg的重物上安装-极轻的细棒(设细棒足够长).如图所示的那样.用手在靠近重物处握住细棒.使重物静止.握细棒的手不动.稍稍减小握力,使手和细棒间保持-定的摩擦力.让重物和细棒保持-定的加速度下落.在起初的1.0s的时间里.重物落下了0.50m.在此过程中手和细棒之间所产生的热量是多少?(g取10m/s2)
在质量为0.5kg的重物上安装-极轻的细棒(设细棒足够长).如图所示的那样.用手在靠近重物处握住细棒.使重物静止.握细棒的手不动.稍稍减小握力,使手和细棒间保持-定的摩擦力.让重物和细棒保持-定的加速度下落.在起初的1.0s的时间里.重物落下了0.50m.在此过程中手和细棒之间所产生的热量是多少?(g取10m/s2)