题目内容
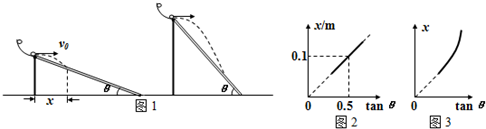
16. 用弹射器从A点竖直向上弹出一质量为m的小球,因受水平方向恒定风力的作用,轨迹如图所示,B、C为小球运动经过的两点,B为轨迹的最高点,C点与A点等高,小球在A、B两点时的速率均为v,不计空气阻力,则( )
用弹射器从A点竖直向上弹出一质量为m的小球,因受水平方向恒定风力的作用,轨迹如图所示,B、C为小球运动经过的两点,B为轨迹的最高点,C点与A点等高,小球在A、B两点时的速率均为v,不计空气阻力,则( )| A. | 小球受水平风力的大小为2mg | |
| B. | AB的水平距离与BC的水平距离之比为1:3 | |
| C. | 小球从A到C的过程中最小动能为$\frac{1}{4}$mv2 | |
| D. | 小球从A到C的过程中机械能增加为$\frac{3}{2}$mv2 |
分析 运用运动的分解法,分别研究水平和竖直两个方向,由牛顿第二定律和位移公式列式,可求水平风力.小球竖直方向做竖直上抛运动,根据对称性确定A到B与B到C的时间关系,由水平方向小球做匀加速运动,求AB的水平距离与BC的水平距离之比.根据动能与时间的关系,由数学知识求最小的速率,从而得到最小动能.由功能关系求小球从A到C的过程中机械能增加量.
解答 解:A、小球从A到B的过程中,竖直方向做竖直上抛运动,水平方向做初速度为零的匀加速直线运动,则
水平方向有:v=at=$\frac{F}{m}$t
竖直方向有:v=gt,联立得:a=g,水平风力 F=mg.故A错误.
B、根据竖直上抛运动的对称性,可知,小球A到B与B到C的时间相等,由于小球水平方向做初速度为零的匀加速直线运动,所以根据匀变速直线运动的推论,可得,AB的水平距离与BC的水平距离之比为1:3,故B正确.
C、小球运动时间t时,速率为 vt=$\sqrt{(v-gt)^{2}+(at)^{2}}$=$\sqrt{(v-gt)^{2}+(gt)^{2}}$,动能为 Ek=$\frac{1}{2}m{v}_{t}^{2}$=$\frac{1}{2}m[(v-gt)^{2}+(gt)^{2}]$=$\frac{1}{2}m(2{g}^{2}{t}^{2}-2vgt+{v}^{2})$
根据数学知识可得,当t=-$\frac{b}{2a}$=$\frac{2vg}{2×2{g}^{2}}$=$\frac{v}{2g}$时Ek有最小值,最小值为 Ekmin=$\frac{1}{4}$mv2.故C正确.
D、小球从A到B的过程中,风力做功 WAB=F•$\overline{AB}$
小球从A到C的过程中,风力做功 WAC=F•$\overline{AC}$,所以WAC=4WAB.
由动能定理得:WAB=$\frac{1}{2}m{v}^{2}$,所以得WAC=2mv2.
由功能关系可得,小球从A到C的过程中机械能增加量等于风力做功,为2mv2.故D错误.
故选:BC
点评 决本题的关键将小球的运动分解为水平方向和竖直方向,理清两个方向上的运动规律,结合牛顿第二定律、动能定理和运动学公式进行求解.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案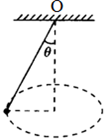 如图所示,长为L的细线拴一个质量为M的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向的夹角为θ,关于小球的受力情况,下列说法正确的是( )
如图所示,长为L的细线拴一个质量为M的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向的夹角为θ,关于小球的受力情况,下列说法正确的是( )| A. | 小球受到重力、线的拉力和向心力三个力 | |
| B. | 向心力由细绳拉力与重力的合力提供 | |
| C. | 向心力的方向指向悬挂点O | |
| D. | 向心力的大小等于$\frac{Mg}{cosθ}$ |
| A. | 开普勒确切描述了行星的运动 | B. | 牛顿发现了万有引力定律 | ||
| C. | 卡文迪许测出了引力常量 | D. | 阿基米德被称为称出地球质量的人 |
| A. | 丹麦天文学家第谷用了20年的时间研究了德国天文学家开普勒的行星观测记录,发现了开普勒行星运动定律 | |
| B. | 德国天文学家伽勒在英国剑桥大学学生亚当斯利用万有引力定律计算出的轨道附近发现了海王星 | |
| C. | 英国物理学家牛顿在实验室里通过几个铅球之间万有引力测量,比较准确地测出了万有引力常量G | |
| D. | 牛顿在思考月球绕地球运行的原因时,苹果偶然落地引起了他的遐想,卡文迪许通过“月-地检验”确立了万有引力定律 |
 如右图所示,木块a、b用一轻弹簧连接起来,放在光滑水平面上,a紧靠在墙壁上,在b上施加向左的水平力F使弹簧压缩,当撤去外力后,下列说法中正确的是( )
如右图所示,木块a、b用一轻弹簧连接起来,放在光滑水平面上,a紧靠在墙壁上,在b上施加向左的水平力F使弹簧压缩,当撤去外力后,下列说法中正确的是( )| A. | a尚未离开墙壁前,a、b与弹簧组成的系统动量守恒 | |
| B. | a尚未离开墙壁前,a、b与弹簧组成的系统机械能不守恒 | |
| C. | a离开墙壁后,a、b与弹簧组成的系统动量守恒 | |
| D. | a离开墙壁后,a、b组成的系统机械能守恒 |

| A. | 落在a点的小球水平速度最小 | |
| B. | 落在b点的小球竖直速度最小 | |
| C. | 落在c点的小球飞行时间最短 | |
| D. | a、b、c三点速度方向的反向延长线交于一点 |
 如图所示,水平传送带AB的长L=18m,传送带以v0=2m/s的速度匀速转动,现将一质量m=2.5kg的小物块(可视为质点)无初速度地放于传送带的A点,最后从B处离开传送带,物块与传送带间的动摩擦因数μ=0.4,取重力加速度昏g=10m/s2.物块由A到B的过程中,求:
如图所示,水平传送带AB的长L=18m,传送带以v0=2m/s的速度匀速转动,现将一质量m=2.5kg的小物块(可视为质点)无初速度地放于传送带的A点,最后从B处离开传送带,物块与传送带间的动摩擦因数μ=0.4,取重力加速度昏g=10m/s2.物块由A到B的过程中,求: