题目内容
10．
一气缸质量为M=60kg（气缸的厚度忽略不计且透热性良好），开口向上放在水平面上，气缸中有横截面积为S=100cm2的光滑活塞，活塞质量m=10kg．气缸内封闭了一定质量的理想气体，此时气柱长度为L1=0.4m．已知大气压为po=1×105Pa．现用力缓慢向上拉动活塞，若使气缸能离开地面，气缸的高度至少是多少？（取重力加速度g=l0m/s2．）
分析 设汽缸足够长，F达最大值时活塞仍在气缸内，根据玻意耳定律求解出拉伸后的长度后比较即可．
解答 解：未加拉力时，活塞受力平衡有：p0S+mg=p1S
代入数据得：${P}_{1}=1.1×1{0}^{5}$Pa，V1=0.4S
设F达到最大值时活塞仍在气缸中，设此时气柱长为L2，气体压强为p2，根据活塞受力平衡，
有：p0S+mg=F+p2S
代入数据得：${P}_{2}=0.4×1{0}^{5}$Pa，V2=L2•S
根据玻意耳定律有：p1SL1=p2SL2
解得：L2=1.1m
答：使气缸能离开地面，气缸的高度至少是1.1m．
点评 本题考查理想气体状态方程应用，关键是找出对应状态的状态参量，明确压强、温度、体积三个量中有几个量变化．
练习册系列答案
中考解读考点精练系列答案
相关题目
20．某辆汽车以相同功率在两种不同的水平路面上行驶，受到的阻力分别为车重的k1和k2倍，最大速率分别为v1和v2，则（ ）
| A． | v2=k1v1 | B． | v2=k2v1 | C． | v2=$\frac{{k}_{2}}{{k}_{1}}$v1 | D． | v2=$\frac{{k}_{1}}{{k}_{2}}$v1 |
如图所示，质量为mA=2kg的滑块A与轻质弹簧拴接在一起．把A、B两滑块拉至最近，使弹簧处于最大压缩状态后用一轻绳绑紧，然后置于光滑水平面上．现将绳烧断，两滑块分开后的速度大小分别为vA=1.5m/s和vB=3m/s．当B与挡板碰撞后原速返回，运动一段时间后再次与弹簧发生相互作用，并拴接在一起．求：
5．
如图所示，有A、B两颗卫星绕地心O做圆周运动，旋转方向相同．A卫星的周期为T1，B卫星的周期为T2，在某一时刻两卫星相距最近，则（引力常量为G）（ ）
如图所示，有A、B两颗卫星绕地心O做圆周运动，旋转方向相同．A卫星的周期为T1，B卫星的周期为T2，在某一时刻两卫星相距最近，则（引力常量为G）（ ）| A． | 两卫星经过时间t=T1+T2再次相距最近 | |
| B． | 两颗卫星的轨道半径之比T22：T12 | |
| C． | 若己知两颗卫星相距最近时的距离，可求出地球的质量 | |
| D． | 若己知两颗卫星相距最近时的距离，可求出地球表面的重力加速度 |
15．
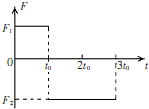一静止的物体所受到的合外力随时间的变化关系如图所示，图中F1、F2未知．已知物体从t=0时刻出发，在3t0时刻恰又返回到出发点，则（ ）
一静止的物体所受到的合外力随时间的变化关系如图所示，图中F1、F2未知．已知物体从t=0时刻出发，在3t0时刻恰又返回到出发点，则（ ）| A． | O～to物体做匀加速直线运动，to-3to物体做匀减速直线运动 | |
| B． | 物体在F1作用下的位移与在F2作用下的位移相等 | |
| C． | t0时刻物体的速度与3t0时刻物体的速度大小之比为$\frac{2}{3}$ | |
| D． | F1与F2大小之比为$\frac{6}{5}$ |
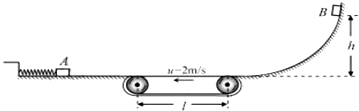
地磁场会对精密仪器中的显像管产生影响．在电子显像管内部，由炽热的灯丝上发射出的电子（可视为初速度为0），在经过电压为U的电场加速后，在不加偏转电场、磁场时，电子（质量为m、电荷量为e，不计重力）应沿直线运动打在荧光屏的正中心位置O．在南极，科考队设备中的显像管由于地磁场的影响，在未加偏转磁场时电子束也会偏离直线运动．设显像管水平放置，地磁场磁感强度的方向竖直向上，大小为B（俯视图如图所示），忽略地磁场对电子在加速过程中的影响，加速电场边缘到荧光屏的距离为l．求在地磁场的影响下：