��Ŀ����
1�� ��ͼ��ʾ�����Ϊ��=37�㣬���L=0.30m���㹻����ƽ�н���������費�ƣ����ڴŸ�ǿ��B=1.0T������ֱ�ڵ���ƽ�����ǿ�ų��У��������˸���һ����ֵR0=2.0���ĵ��裮��ƽ�е������һ������������������m=1.0kg������r=2.0�����뵼���Ķ�Ħ��������=0.50����������ƽ���ڵ������ϵij��ٶ�v0=10m/s�ϻ�����֪����������ߵ�Ĺ����У�ͨ���϶˵���ĵ���q=0.10C��ȡg=10m/s2����
��ͼ��ʾ�����Ϊ��=37�㣬���L=0.30m���㹻����ƽ�н���������費�ƣ����ڴŸ�ǿ��B=1.0T������ֱ�ڵ���ƽ�����ǿ�ų��У��������˸���һ����ֵR0=2.0���ĵ��裮��ƽ�е������һ������������������m=1.0kg������r=2.0�����뵼���Ķ�Ħ��������=0.50����������ƽ���ڵ������ϵij��ٶ�v0=10m/s�ϻ�����֪����������ߵ�Ĺ����У�ͨ���϶˵���ĵ���q=0.10C��ȡg=10m/s2������1���������������ٶȣ�
��2�����������������߶�h��
��3�����������������϶˵���R0���ͷŵĽ����ȣ�
���� ��1����������»��������У��ܵ������������֧����������Ħ�����Ͱ������������������ٶȵ����������֪��ab�տ�ʼ�˶�ʱ�����ļ��ٶȣ�
��2��Ӧ�õ����Ķ���ʽ����������Ȼ���������������˶������λ�ƣ���������������߶ȣ�
��3��������������˶�ʱ���ٶ�����������غ㶨����������в�����������
��� �⣺��1���������������Ĺ��̣��и�Ÿ��߲����ĸ�Ӧ�綯��Ϊ��E=BL�ԣ�
��·���ܵ���Ϊ��R=r+$\frac{{R}_{0}}{2}$=2+$\frac{2}{2}$=3����
��·�еĸ�Ӧ����Ϊ��I=$\frac{E}{R}$=$\frac{BLv}{R}$��
�������ܵ�ƽ���ڵ������µİ�����Ϊ��F����=BIL=$\frac{{B}^{2}{L}^{2}v}{R}$��
���������ܵ�ƽ���ڵ������µ�����mgsin�ȡ�����Ħ����Ϊ��f=��mgcos�ȣ�
��ţ���˶����ɿ�֪��mgsin��+��mgcos��+$\frac{{B}^{2}{L}^{2}v}{R}$=ma��
���������������е������ٶȶ�Ӧ���ǽ�����������ٶȣ����������������������˶���
���Խ��������������е������ٶȾ����ٶ�Ϊ��0��˲���У�amax=g��sin��+��gcos�ȣ�+$\frac{{B}^{2}{L}^{2}{v}_{0}}{mR}$��
��ã������ٶ�Ϊ��amax=10.3m/s2��
��2����������������ߵ�Ĺ����У�ͨ���϶˵���ĵ�����q=0.1C��
��������ͨ���ĵ���Ϊ��2q=$\overline{I}$��t=$\frac{\overline{E}}{R}$��t=$\frac{\frac{����}{��t}}{R}$��t=$\frac{BLs}{R}$��
�������ص���������������Ϊ��s=$\frac{2qR}{BL}$=$\frac{2��0.1��3}{1��0.3}$=2m��
���������������߶ȣ�h=ssin��=2��sin37��=1.2m��
��3���϶˵������¶˵�����ȣ����������Ϊ1��������������ĵ���r=2��������
���·�Dz����Ľ�����Ϊȫ��·�����ȵ�$\frac{1}{3}$���϶˵���Ľ�����Q��Ϊ���·�����ȵ�$\frac{1}{2}$��
ȫ��·�����Ľ�����Ϊ6Q���������غ��֪��mg��sin��+��cos�ȣ�s+6Q=$\frac{1}{2}$mv02����ã�Q=5J��
�𣺣�1���������������ٶ�Ϊ10.3m/s2��
��2�����������������߶�hΪ1.2m��
��3�����������������϶˵���R0���ͷŵĽ�����Ϊ5J��
���� ��Ÿ�Ӧ�е����и�����ĸ�Ӧ�綯���ڿ������漰�϶࣬�ؼ�Ҫ��ȷ����������������������ƽ�����������ܹ�ϵ������⣮

 ��ͼ��ʾ�����ν�����������ǿ�ų��У�efΪһ�����������ab��cd�们�����Ӵ����ã���Ÿ�Ӧǿ��ΪB��ac��ΪL���ڡ�tʱ�����������ٻ��������d���ɷ����ڵ�Ÿ�Ӧ����E=n$\frac{����}{��t}$��֪������˵����ȷ���ǣ�������
��ͼ��ʾ�����ν�����������ǿ�ų��У�efΪһ�����������ab��cd�们�����Ӵ����ã���Ÿ�Ӧǿ��ΪB��ac��ΪL���ڡ�tʱ�����������ٻ��������d���ɷ����ڵ�Ÿ�Ӧ����E=n$\frac{����}{��t}$��֪������˵����ȷ���ǣ�������| A�� | ��ef����ʱ������������L��d���Ҳ��������L��d�����E=$\frac{2BL��d}{��t}$ | |
| B�� | ��ef����ʱ������������L��d���Ҳ��������L��d��������������E=0 | |
| C�� | �ڹ�ʽE=n$\frac{����}{��t}$�У����и�Ÿ�������£�����=B��S����SӦ�ǵ�����и�Ÿ���ɨ������������E=$\frac{BL��d}{��t}$ | |
| D�� | ���и�Ÿ��ߵ�����£�ֻ����E=BLv���㣬������E=n$\frac{����}{��t}$���� |
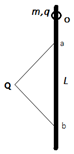 ��ͼ��ʾ��LΪ��ֱ�̶��Ĺ⻬��Ե�ˣ�����O������һ����Ϊm�������Ϊq�Ĵ�����С�����ڸ˵����̶�һ�����ΪQ�������ɣ�����ab���㵽���ɵľ�����ȣ���С����ͼʾλ�õ�O���ɾ�ֹ�ͷţ�������˵����ȷ���ǣ�������
��ͼ��ʾ��LΪ��ֱ�̶��Ĺ⻬��Ե�ˣ�����O������һ����Ϊm�������Ϊq�Ĵ�����С�����ڸ˵����̶�һ�����ΪQ�������ɣ�����ab���㵽���ɵľ�����ȣ���С����ͼʾλ�õ�O���ɾ�ֹ�ͷţ�������˵����ȷ���ǣ�������| A�� | С����O�㵽b����˶������п��ܴ�������ƽ��� | |
| B�� | С����O�㵽b����˶����̣��糡�����Ĺ�����Ϊ�� | |
| C�� | С����O��a��֮����ٶ�һ����������С | |
| D�� | С����O��b��֮����ٶ�һ���ȼ�С������ |
| A�� | �綯����Ȧ����������ΪI2Rt | B�� | �綯����Ȧ����������Ϊ$\frac{{U}^{2}t}{R}$ | ||
| C�� | �綯�����ĵĵ���Ϊ$\frac{{U}^{2}t}{R}$ | D�� | �綯������Ļ�е��ΪUIt |
| A�� | $\frac{{{a_1}{t_1}+{a_2}{t_2}}}{4}$ | B�� | $\frac{{{a_2}{t_2}}}{2}$ | ||
| C�� | $\frac{{{a_1}{t_1}^2+{a_2}{t_2}^2}}{{2��{{t_1}+{t_2}}��}}$ | D�� | $\frac{{{a_1}{t_1}+{a_2}{t_2}}}{2}$ |
 ��ͼ��ʾ����ˮƽ����������ƽ�н�������MN��PQ��������Ϊd����ǿ�ų���ֱ�ڵ������ڵ�ƽ������Ÿ�Ӧǿ�ȴ�СΪB��������ȫ��ͬ�Ľ�����1��2���һ���ľ���ڷ��ڵ����ϣ����뵼�촹ֱ�����ǵĵ����ΪR�������뵼��Ӵ����ã�������費�ƣ������˵�Ħ�����ƣ���1�Գ��ٶ�v0�����2��Ϊʹ���˲����������2�̶��벻�̶���������£�����ڷ�����ʱ�����پ���֮��Ϊ��������
��ͼ��ʾ����ˮƽ����������ƽ�н�������MN��PQ��������Ϊd����ǿ�ų���ֱ�ڵ������ڵ�ƽ������Ÿ�Ӧǿ�ȴ�СΪB��������ȫ��ͬ�Ľ�����1��2���һ���ľ���ڷ��ڵ����ϣ����뵼�촹ֱ�����ǵĵ����ΪR�������뵼��Ӵ����ã�������費�ƣ������˵�Ħ�����ƣ���1�Գ��ٶ�v0�����2��Ϊʹ���˲����������2�̶��벻�̶���������£�����ڷ�����ʱ�����پ���֮��Ϊ��������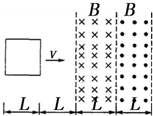 �⻬��ˮƽ�����Ϸ����ڿ��Ⱦ�ΪL=0.5m���Ÿ�Ӧǿ�Ⱦ�ΪB=1T�����������෴���н���ǿ�ų����ų�����ֱ���ֱ���º����ϣ���ͼ��ʾ���ڴų�����������һ�߳�L=0.5m�������ε����߿��߿��Ҳ��ų��߽�ҲΪL=0.5m���߿��ܵ���ΪR=2������ʹ�߿���������v=2m/s���ٶ����ٴ����ų����涨�߿�����ʱ�뷽��ĵ����͵綯��Ϊ������ͨ����������Ϊ������������߿��еĸ�Ӧ�綯�ơ���Ӧ�������繦�ʺʹ����߿�Ĵ�ͨ��������ͼ����ȷ���ǣ�������
�⻬��ˮƽ�����Ϸ����ڿ��Ⱦ�ΪL=0.5m���Ÿ�Ӧǿ�Ⱦ�ΪB=1T�����������෴���н���ǿ�ų����ų�����ֱ���ֱ���º����ϣ���ͼ��ʾ���ڴų�����������һ�߳�L=0.5m�������ε����߿��߿��Ҳ��ų��߽�ҲΪL=0.5m���߿��ܵ���ΪR=2������ʹ�߿���������v=2m/s���ٶ����ٴ����ų����涨�߿�����ʱ�뷽��ĵ����͵綯��Ϊ������ͨ����������Ϊ������������߿��еĸ�Ӧ�綯�ơ���Ӧ�������繦�ʺʹ����߿�Ĵ�ͨ��������ͼ����ȷ���ǣ�������


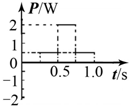
 ��1����ͼ1��ʾ���̶���ˮƽ���ϵĽ������abcd��������ֱ���µ���ǿ�ų��У�������MN�ؿ�����ٶ�v�����������˶�����ܵ�ab��dcƽ�У�bc��ab��dc��ֱ��MN��bc�ij��Ⱦ�Ϊl�����˶�������MNʼ����bcƽ�У������ܱ������ýӴ����ų��ĴŸ�Ӧǿ��ΪB��
��1����ͼ1��ʾ���̶���ˮƽ���ϵĽ������abcd��������ֱ���µ���ǿ�ų��У�������MN�ؿ�����ٶ�v�����������˶�����ܵ�ab��dcƽ�У�bc��ab��dc��ֱ��MN��bc�ij��Ⱦ�Ϊl�����˶�������MNʼ����bcƽ�У������ܱ������ýӴ����ų��ĴŸ�Ӧǿ��ΪB�� ��ͼ�ǰ���ʾ��ͼ����CEˮƽ��CA��ֱ������DE��ˮƽ����ɦ��ǣ���BC����ֱ����ɦ½ǣ�����E��ʩ����ֱ���µĴ�СΪF���������ã���CA�����ϰ������Ĵ�СΪ$\frac{F}{tan��•tan��}$��
��ͼ�ǰ���ʾ��ͼ����CEˮƽ��CA��ֱ������DE��ˮƽ����ɦ��ǣ���BC����ֱ����ɦ½ǣ�����E��ʩ����ֱ���µĴ�СΪF���������ã���CA�����ϰ������Ĵ�СΪ$\frac{F}{tan��•tan��}$��