题目内容
11. 两列简谐横波分别沿x轴正方向和负方向传播,波速均为v=1m/s,波源的振幅均为A=2cm,如图所示为t=0时刻两列波的图象,此刻平衡位置在x=0.2m和x=0.8m的P、Q两质点恰好开始振动,质点M的平衡位置位于x=0.5m处,求:
两列简谐横波分别沿x轴正方向和负方向传播,波速均为v=1m/s,波源的振幅均为A=2cm,如图所示为t=0时刻两列波的图象,此刻平衡位置在x=0.2m和x=0.8m的P、Q两质点恰好开始振动,质点M的平衡位置位于x=0.5m处,求:(ⅰ)两列波相遇的时刻t为多少?
(ⅱ)当t=0.6s时,质点M的位移.
分析 (i)两列简谐波的传播速度相等,在介质中都匀速传播,由运动学公式求解时间.
(ii)M位于PQ的中点,两列波相遇时M点振动加强,结合M点开始振动时间,从而求得M点的位移.
解答 解:(i)两列简谐波的波前相距 s=0.6m,
由s=2vt得:t=$\frac{s}{2v}$=$\frac{0.6}{2×1}$s=0.3s
即两列波相遇的时刻 t=0.3s
(ii)由于两列波波速、波长均相等,所以周期也相等,
周期为 T=$\frac{λ}{v}$=$\frac{0.4}{1}$=0.4s,M点起振方向向下.
当t=0.6s时,质点M已经振动了0.3s=$\frac{3}{4}$T
所以当t=0.6s时,质点M到达波峰,其位移为 y=4cm
答:(ⅰ)两列波相遇的时刻t为0.3s.
(ⅱ)当t=0.6s时,质点M的位移是4cm.
点评 本题要理解波的叠加原理,知道当该波的波峰与波峰相遇时,此处相对平衡位置的位移为振幅的二倍;当波峰与波谷相遇时此处的位移为零,注意第二问是求得M点的位移,不是M点的路程.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
16.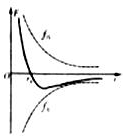 分子力F随分子之间的距离变化的关系如图所示,下列关于分子力f和分子势能的说法正确的是( )
分子力F随分子之间的距离变化的关系如图所示,下列关于分子力f和分子势能的说法正确的是( )
 分子力F随分子之间的距离变化的关系如图所示,下列关于分子力f和分子势能的说法正确的是( )
分子力F随分子之间的距离变化的关系如图所示,下列关于分子力f和分子势能的说法正确的是( )| A. | 当r=r0时,分子力为零,分子势能最大 | |
| B. | 当r<r0时,随r减小,分子力增大,分子势能减小 | |
| C. | 当r>r0时,随r增大,分子力减小,分子势能增大 | |
| D. | 当r>r0时,随r增大,分子力先增大后减小,分子势能增大 |
3.做曲线运动的物体一定改变的是( )
| A. | 速度的大小 | B. | 速度的方向 | C. | 加速度的大小 | D. | 加速度的方向 |
20. 质量为2kg的物体在水平面xoy上运动,在y方向的速度-时间图象和x方向的位移-时间图象如图所示,下列说法正确的是( )
质量为2kg的物体在水平面xoy上运动,在y方向的速度-时间图象和x方向的位移-时间图象如图所示,下列说法正确的是( )
 质量为2kg的物体在水平面xoy上运动,在y方向的速度-时间图象和x方向的位移-时间图象如图所示,下列说法正确的是( )
质量为2kg的物体在水平面xoy上运动,在y方向的速度-时间图象和x方向的位移-时间图象如图所示,下列说法正确的是( )| A. | 物体的合运动是匀加速直线运动 | B. | 物体所受的合外力为12N | ||
| C. | 物体的初速度大小为4m/s | D. | 1s末物体速度大小为5m/s |
 如图所示,在匀强电场中,用一根绝缘的细线悬挂一质量为m的小球,小球带正电,电量为q,静止时细线与竖直方向的夹角为θ,求所加匀强电场的场强最小值为多少?方向怎样?
如图所示,在匀强电场中,用一根绝缘的细线悬挂一质量为m的小球,小球带正电,电量为q,静止时细线与竖直方向的夹角为θ,求所加匀强电场的场强最小值为多少?方向怎样? 如图,在真空中有一平行玻璃砖,一束单色光从光源P发出与界面成θ=30°角从ab面中点射入,测得折射角α=45°,在玻璃砖的某个侧面射出,假设光源P到ab面上O的传播时间和它在玻璃砖中传播的时间相等,已知光在真空中的传播速度C=3.0×108m/s,ab长为$\sqrt{3}$×10cm.求:
如图,在真空中有一平行玻璃砖,一束单色光从光源P发出与界面成θ=30°角从ab面中点射入,测得折射角α=45°,在玻璃砖的某个侧面射出,假设光源P到ab面上O的传播时间和它在玻璃砖中传播的时间相等,已知光在真空中的传播速度C=3.0×108m/s,ab长为$\sqrt{3}$×10cm.求: