题目内容
3. 如图所示,极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道,地球看作均匀球体).若已知一颗极地卫星从北纬300的正上方,按图示方向第一次运行至赤道正上方时所用的时间为0.25h,则同步卫星的线速度v1和该极地卫星的线速度v2大小之比为( )
如图所示,极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道,地球看作均匀球体).若已知一颗极地卫星从北纬300的正上方,按图示方向第一次运行至赤道正上方时所用的时间为0.25h,则同步卫星的线速度v1和该极地卫星的线速度v2大小之比为( )| A. | $\frac{1}{\sqrt{2}}$ | B. | $\frac{\sqrt{2}}{1}$ | C. | $\frac{1}{2}$ | D. | 2 |
分析 根据极地卫星的运动轨迹,判断极地卫星的周期,卫星运动的向心力由地球对卫星的万有引力提供,解出卫星的周期与轨道半径的关系和线速度与轨道板机的关系,据此进行解答.
解答 解:从北纬30°的正上方按图示方向第一次运行至南纬60°正上方转过的圆心角为θ=$\frac{π}{2}$,用时0.75h,故该极地卫星的周期为 T2=3h.
而同步卫星的周期为T1=24h,
由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$得,v=$\sqrt{\frac{GM}{r}}$
可得:$\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{{r}_{2}}{{r}_{1}}}$
由开普勒第三定律得:$\frac{{T}_{1}^{2}}{{T}_{2}^{2}}$=$\frac{{r}_{1}^{3}}{{r}_{2}^{3}}$=64
故有:$\frac{{r}_{1}}{{r}_{2}}$=$\frac{4}{1}$
解得:$\frac{{v}_{1}}{{v}_{2}}$=$\frac{1}{2}$
故选:C.
点评 卫星的线速度v=$\sqrt{\frac{GM}{r}}$和周期公式T=$\frac{2πr}{v}$.灵活运运用万有引力提供圆周运动的向心力,要能够熟练的解出轨道半径与周期和线速度的关系是解决本题的关键.

练习册系列答案
相关题目
19.均匀小球A、B质量分别为m,4m,球心相距为R,引力常量为G,则A球受到B球的万有引力大小是( )
| A. | G$\frac{{4{m^2}}}{R^2}$ | B. | G$\frac{{4{m^2}}}{{{R^{\;}}}}$ | C. | G$\frac{m^2}{{{R^{\;}}}}$ | D. | G$\frac{m^2}{R^2}$ |
18.质量为m的跳水运动员,从离水面高h的跳台上以速度v1斜向上跳起,跳起的最大高度为H(离跳台),最后又以速度v2进入水池中,不计空气阻力,则运动员起跳时所做的功是( )
| A. | $\frac{1}{2}$mv12 | B. | mg(H+h) | C. | $\frac{1}{2}$mv12+mgh | D. | $\frac{1}{2}$mv22-mgh |
8.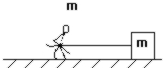 一只猴子用绳子拉着一块与其等质量的石块,在光滑水平面上运动(如图),开始时猴子和石块都静止,然后猴子以相对于绳子的速度u拉石块,则石块的速度为( )
一只猴子用绳子拉着一块与其等质量的石块,在光滑水平面上运动(如图),开始时猴子和石块都静止,然后猴子以相对于绳子的速度u拉石块,则石块的速度为( )
 一只猴子用绳子拉着一块与其等质量的石块,在光滑水平面上运动(如图),开始时猴子和石块都静止,然后猴子以相对于绳子的速度u拉石块,则石块的速度为( )
一只猴子用绳子拉着一块与其等质量的石块,在光滑水平面上运动(如图),开始时猴子和石块都静止,然后猴子以相对于绳子的速度u拉石块,则石块的速度为( )| A. | $\frac{u}{2}$ | B. | u | C. | $\frac{3}{2}u$ | D. | 2u |
15.近年我国高速铁路技术得到飞速发展,国产新型CRH380D动车组列车在沪宁高铁上载客运行,其设计最高运营时速为380公里.对提高铁路运行速度的以下说法,错误的是( )
| A. | 减少路轨阻力,有利于提高列车最高时速 | |
| B. | 当列车保持最高时速行驶时,其牵引力与阻力大小相等 | |
| C. | 列车的最高时速取决于其最大功率、阻力及相关技术 | |
| D. | 将列车车头做成流线形,减小空气阻力,有利于提高列车功率 |
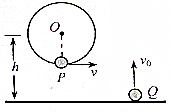 如图所示,小球P固定于圆盘上,小球Q位于地面上,开始时小球P从圆盘的最低点绕圆盘的圆心做匀速圆周运动,同时小球Q以初速度v0=8m/s做竖直上抛运动,已知圆盘的圆心离地面的高h=2.4m,g=10m/s2,在运动过程中发现两小球在同一高度有速度相等的情况存在,问圆盘的半径是多大?
如图所示,小球P固定于圆盘上,小球Q位于地面上,开始时小球P从圆盘的最低点绕圆盘的圆心做匀速圆周运动,同时小球Q以初速度v0=8m/s做竖直上抛运动,已知圆盘的圆心离地面的高h=2.4m,g=10m/s2,在运动过程中发现两小球在同一高度有速度相等的情况存在,问圆盘的半径是多大?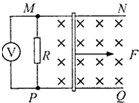 如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距l=0.2m,电阻R=0.4Ω,导轨上静止放置一质量m=0.1kg、电阻r=0.1Ω的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度B=0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,杆以加速度a=2m/s2匀加速运动5秒
如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距l=0.2m,电阻R=0.4Ω,导轨上静止放置一质量m=0.1kg、电阻r=0.1Ω的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度B=0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,杆以加速度a=2m/s2匀加速运动5秒