题目内容
11.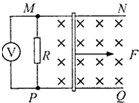 如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距l=0.2m,电阻R=0.4Ω,导轨上静止放置一质量m=0.1kg、电阻r=0.1Ω的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度B=0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,杆以加速度a=2m/s2匀加速运动5秒
如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距l=0.2m,电阻R=0.4Ω,导轨上静止放置一质量m=0.1kg、电阻r=0.1Ω的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度B=0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,杆以加速度a=2m/s2匀加速运动5秒(1)5s末时电阻R上消耗的电功率;
(2)金属杆在5s末的运动速率;
(3)5s末时外力F的功率.
(4)5秒整个过程中,整个闭合电路中产生的热量.
分析 (1)(2)杆以加速度a=2m/s2匀加速运动5秒,由v=at求出速度,由E=BLv求出电动势,由闭合电路的欧姆定律求出电流值,由公式P=I2R求R上消耗的电功率;
(3)由F安=BIL求出安培力,由牛顿第二定律和运动学公式求出外力F,外力功率P=Fv.
(4)拉力做的功转化为棒的动能和整个闭合电路中产生的热量,由功能关系即可求得结果.
解答 解:(1)(2)由题意,5s末时杆的速度:v=at=2×5=10m/s
产生的电动势:E=Blv=0.5×0.2×10=1V
回路中的电流:I=$\frac{E}{R+r}=\frac{1}{0.4+0.1}=2$A
电阻R上消耗的电功率:PR=I2R=22×0.4=1.6W
(3)5s末时杆所受的安培力为 F安=BIl=0.5×2×0.2=0.2N
根据牛顿第二定律得
F-F安=ma,
代入数据解得,F=0.4N
则外力F的功率为 P=Fv=0.4×10=4W
(4)5s内拉力做的功转化为棒的动能和整个闭合电路中产生的热量,由功能关系得:
$Pt=Q+\frac{1}{2}m{v}^{2}$
所以:Q=Pt-$\frac{1}{2}m{v}^{2}$=4×5-$\frac{1}{2}×0.1×1{0}^{2}$=15J
答:(1)5s末时电阻R上消耗的电功率是1.6W.
(2)金属杆在5s末的运动速度是10m/s.
(3)5s末时外力F的功率是4W.
(4)5秒整个过程中,整个闭合电路中产生的热量是15J.
点评 本题是电磁感应与电路、力学知识的综合,由电路的串联关系先求出电动势,再求出速度;由加速度的定义,求出加速度;根据瞬时功率的表达式,求出第5秒末外力F的功率.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7. 如图所示,质量为m的冰壶,与水平冰面间动摩擦因数为μ,被运动员以初速度v推出后,沿直线走了距离s后停止,下列说法中正确的有( )
如图所示,质量为m的冰壶,与水平冰面间动摩擦因数为μ,被运动员以初速度v推出后,沿直线走了距离s后停止,下列说法中正确的有( )
 如图所示,质量为m的冰壶,与水平冰面间动摩擦因数为μ,被运动员以初速度v推出后,沿直线走了距离s后停止,下列说法中正确的有( )
如图所示,质量为m的冰壶,与水平冰面间动摩擦因数为μ,被运动员以初速度v推出后,沿直线走了距离s后停止,下列说法中正确的有( )| A. | 摩擦力对冰壶做正功μmgs | B. | 冰壶克服摩擦力做功 | ||
| C. | 冰壶加速度大小为μg | D. | 合外力对冰壶做正功 |
16. 如图所示,cb为固定在小车上的水平横杆,物块M穿在杆上,靠摩擦力保持相对杆静止,M又通过轻细线悬吊着一个小铁球m,此时小车正以大小为a的加速度向右做匀加速运动,而M、m均相对小车静止,细线与竖直方向的夹角为θ.小车的加速度逐渐增大,M始终和小车保持相对静止,当加速度增加到2a时,下列说法正确的是( )
如图所示,cb为固定在小车上的水平横杆,物块M穿在杆上,靠摩擦力保持相对杆静止,M又通过轻细线悬吊着一个小铁球m,此时小车正以大小为a的加速度向右做匀加速运动,而M、m均相对小车静止,细线与竖直方向的夹角为θ.小车的加速度逐渐增大,M始终和小车保持相对静止,当加速度增加到2a时,下列说法正确的是( )
 如图所示,cb为固定在小车上的水平横杆,物块M穿在杆上,靠摩擦力保持相对杆静止,M又通过轻细线悬吊着一个小铁球m,此时小车正以大小为a的加速度向右做匀加速运动,而M、m均相对小车静止,细线与竖直方向的夹角为θ.小车的加速度逐渐增大,M始终和小车保持相对静止,当加速度增加到2a时,下列说法正确的是( )
如图所示,cb为固定在小车上的水平横杆,物块M穿在杆上,靠摩擦力保持相对杆静止,M又通过轻细线悬吊着一个小铁球m,此时小车正以大小为a的加速度向右做匀加速运动,而M、m均相对小车静止,细线与竖直方向的夹角为θ.小车的加速度逐渐增大,M始终和小车保持相对静止,当加速度增加到2a时,下列说法正确的是( )| A. | 横杆对M的摩擦力增加到原来的2倍 | |
| B. | 横杆对M的弹力增大 | |
| C. | 细线与竖直方向的夹角增加到原来的2倍 | |
| D. | 细线的拉力增加到原来的2倍 |
3. 如图所示,极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道,地球看作均匀球体).若已知一颗极地卫星从北纬300的正上方,按图示方向第一次运行至赤道正上方时所用的时间为0.25h,则同步卫星的线速度v1和该极地卫星的线速度v2大小之比为( )
如图所示,极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道,地球看作均匀球体).若已知一颗极地卫星从北纬300的正上方,按图示方向第一次运行至赤道正上方时所用的时间为0.25h,则同步卫星的线速度v1和该极地卫星的线速度v2大小之比为( )
 如图所示,极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道,地球看作均匀球体).若已知一颗极地卫星从北纬300的正上方,按图示方向第一次运行至赤道正上方时所用的时间为0.25h,则同步卫星的线速度v1和该极地卫星的线速度v2大小之比为( )
如图所示,极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道,地球看作均匀球体).若已知一颗极地卫星从北纬300的正上方,按图示方向第一次运行至赤道正上方时所用的时间为0.25h,则同步卫星的线速度v1和该极地卫星的线速度v2大小之比为( )| A. | $\frac{1}{\sqrt{2}}$ | B. | $\frac{\sqrt{2}}{1}$ | C. | $\frac{1}{2}$ | D. | 2 |
20.两颗人造地球卫星离地面的高度不同,则下列说法正确的是( )
| A. | 离地面高的周期小 | B. | 离地面高的周期大 | ||
| C. | 它们的周期一样大 | D. | 无法确定 |
1.如图所示,一个球绕中心轴OO′以角速度ω转动,则( )


| A. | A、B两点的加速度相等 | B. | A、B两点的线速度大小相等 | ||
| C. | 若α=30°,则vA:vB=$\sqrt{3}$:2 | D. | 若α=30°,则VA:VB=1:2 |

 半圆形光滑轨道半径为R,固定在水平地面上,并使其轨道平面与地面垂直,如图所示,物体m1、m2同时由轨道左、右最高点释放,二者碰后粘在一起向上运动,求它们能上升的最大高度?
半圆形光滑轨道半径为R,固定在水平地面上,并使其轨道平面与地面垂直,如图所示,物体m1、m2同时由轨道左、右最高点释放,二者碰后粘在一起向上运动,求它们能上升的最大高度?