题目内容
13. 如图,用“碰撞实验器”研究两个小球在轨道水平部分碰撞前后的动量关系.
如图,用“碰撞实验器”研究两个小球在轨道水平部分碰撞前后的动量关系.(1)关于入射小球在斜槽上释放点的高低对实验的影响,下列说法正确的是C.
A.释放点越低,小球受阻力越小,入射小球速度越小,误差越小
B.释放点越低,两球碰后水平位移越小,水平位移测量的相对误差越小,两球速度的测量越准确
C.释放点越高,两球相碰时相互作用的内力越大,碰撞前后动量之差越小,误差越小
D.释放点越高,入射小球对被碰小球的作用力越大,轨道对被碰小球的阻力越小
(2)已知入射球与被碰小球的质量分别为m1、m2,图中O点是小球抛出点在地面上的垂直投影,图中P点是入射球m1单独释放时的平均落点,M、N两点是入射球m1与被碰小球m2碰撞后落点的平均位置,测得OP、OM、ON的距离分别为x1、x2、x3.
若两球相碰前后的动量守恒,其表达式可表示为m1•OM+m2•ON=m1•OP;
若碰撞是弹性碰撞,那么还应满足的表达式为${m}_{1}•{\overline{OM}}^{2}+{m}_{2}•{\overline{ON}}^{2}={m}_{1}•{\overline{OP}}^{2}$.
分析 (1)通过实验的原理知道小球碰撞后做平抛运动,抓住平抛运动的时间相等,小球飞行的水平距离来代表小球的水平速度来验证动量守恒定律.
释放点越低,入射小球速度小,读数的相对误差大,
释放点越高,两球相碰时相互作用的内力越大,碰撞前后系统的动量之差越小,误差越小.
(2)根据实验的原理好,结合平抛运动的特点列式即可.
解答 解:(1)A、释放点越低,入射小球速度小,两球碰后水平位移越小,水平位移测量的相对读数的相对误差大,故AB错误;
C、释放点越高,两球相碰时,相互作用的内力越大,碰撞前后动量之差越小,误差越小,故C正确,
D、释放点越高,入射小球对被碰小球的作用力越大,支柱对被碰小球的阻力不变,阻力的影响相对越小,可以较好地满足动量守恒的条件,也有利于减小测量水平位移时的相对误差,从而使实验的误差减小,故D错误;
故选:C.
(2)设落地时间为t,则v1=$\frac{OP}{t}$,${v′}_{1}=\frac{OM}{t}$,${v′}_{2}=\frac{ON}{t}$
而动量守恒的表达式是m1v1=m1v1′+m2v2′
所以若两球相碰前后的动量守恒,则m1•OM+m2•ON=m1•OP 成立
若碰撞是弹性碰撞,动能是守恒的,则有:$\frac{1}{2}$m1v12=$\frac{1}{2}$m1v1′2+$\frac{1}{2}$m2v2′2
即${m}_{1}•{\overline{OM}}^{2}+{m}_{2}•{\overline{ON}}^{2}={m}_{1}•{\overline{OP}}^{2}$成立
故答案为:(1)C;(2)m1•OM+m2•ON=m1•OP;${m}_{1}•{\overline{OM}}^{2}+{m}_{2}•{\overline{ON}}^{2}={m}_{1}•{\overline{OP}}^{2}$
点评 本实验主要是要把动量守恒用水平方向的位移表示出来,同学们一定要注意掌握,因为这是本实验的一个重要的技巧.

 小学课时特训系列答案
小学课时特训系列答案| A. | 电源电动势的大小,等于电源没有接入电路时电源两极间的电压的大小,所以当电源接入电路时,电动势大小将发生变化 | |
| B. | 闭合电路中,并联在电源两端的电压表的示数就是电源电动势的值 | |
| C. | 电源的电动势是表示电源把其它形式的能转化为电能的本领的大小的物理量 | |
| D. | 在闭合电路中,电源的内电压就等于电源两端的电压 |
| A. | 月球表面上物体的重力加速度和地球公转的向心加速度 | |
| B. | 月球表面上物体的重力加速度和地球表面上物体的重力加速度 | |
| C. | 月球公转的向心加速度和地球公转的向心加速度 | |
| D. | 月球公转的向心加速度和地球表面上物体的重力加速度 |
| A. | 彗星绕太阳运动的角速度不变 | |
| B. | 彗星在近日点处的线速度大于远日点处的线速度 | |
| C. | 彗星在近日点处的加速度大于远日点处的加速度 | |
| D. | 彗星在近日点处的机械能小于远日点处的机械能 |
| A. | 光电效应现象表明光具有粒子性 | |
| B. | 裂变物质体积小于临界体积时,链式反应不能进行 | |
| C. | 电子可以在原子核外任意半径的圆轨道上运动 | |
| D. | 温度升高时原子运动加剧,半衰期变短 |
 如图所示,曲轴上挂一个弹簧振子,转动摇把曲轴可带动弹簧振子上下振动,开始时不转动摇把,让振子自由振动,测得其频率为2Hz,现匀速转动摇把且转速为4r/s,当弹簧振子稳定振动时,其振动频率为4Hz;若要使其振动稳定时振幅最大,摇把的转速需为2r/s.
如图所示,曲轴上挂一个弹簧振子,转动摇把曲轴可带动弹簧振子上下振动,开始时不转动摇把,让振子自由振动,测得其频率为2Hz,现匀速转动摇把且转速为4r/s,当弹簧振子稳定振动时,其振动频率为4Hz;若要使其振动稳定时振幅最大,摇把的转速需为2r/s.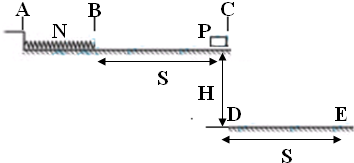
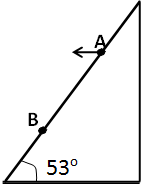 如图所示,在倾角为53°的斜坡上,从A点水平抛出一个物体,物体落在斜坡的B点,测得AB两点间的距离是S=25m,求:(sin53°=0.8,cos53°=0.6,g=10m/s2)
如图所示,在倾角为53°的斜坡上,从A点水平抛出一个物体,物体落在斜坡的B点,测得AB两点间的距离是S=25m,求:(sin53°=0.8,cos53°=0.6,g=10m/s2)