题目内容
4. “拔火罐”是一种中医疗法,为了探究“火罐”内的温度,某人设计了如图实验.圆柱状薄壁气缸(横截面积为S)被固定在铁架台上,轻质活塞通过细线与重物m相连,将一团燃烧的轻质酒精棉球从缸底的开关K处扔到气缸内,酒精棉球熄灭时密闭开关K,此时活塞下的细线刚好拉直且拉力为零,而这时活塞距缸底为L.由于气缸传热良好,随后重物会被吸起,最后重物稳定在距地面$\frac{L}{10}$处.已知环境温度为27℃不变,$\frac{mg}{s}$与$\frac{1}{6}$大气压强相当,气缸内的气体可看做理想气体,问酒精棉球熄灭时气缸内的温度为多少摄氏度?
“拔火罐”是一种中医疗法,为了探究“火罐”内的温度,某人设计了如图实验.圆柱状薄壁气缸(横截面积为S)被固定在铁架台上,轻质活塞通过细线与重物m相连,将一团燃烧的轻质酒精棉球从缸底的开关K处扔到气缸内,酒精棉球熄灭时密闭开关K,此时活塞下的细线刚好拉直且拉力为零,而这时活塞距缸底为L.由于气缸传热良好,随后重物会被吸起,最后重物稳定在距地面$\frac{L}{10}$处.已知环境温度为27℃不变,$\frac{mg}{s}$与$\frac{1}{6}$大气压强相当,气缸内的气体可看做理想气体,问酒精棉球熄灭时气缸内的温度为多少摄氏度?
分析 酒精棉球熄灭后,以活塞为研究对象可求出封闭气体初末状态压强,利用理想气体状态方程列式即可求解.
解答 解:设酒精棉球熄灭时气缸内的温度为t,气缸内封闭气体的状态为:
P1=P0 V1=LS T1=237+t
重物稳定气缸内封闭气体的状态为:
${P}_{2}={P}_{0}-\frac{mg}{S}=\frac{5}{6}{P}_{0}$ ${V}_{2}=\frac{9}{10}$LS,T2=300 K
由理想气体状态方程:$\frac{{P}_{1}{V}_{1}}{{T}_{1}}=\frac{{P}_{2}{V}_{2}}{{T}_{2}}$
解得:t=127°C
答:酒精棉球熄灭时气缸内的温度为127摄氏度
点评 本题得关键是以活塞为研究对象,受力分析利用平衡求出初末状态压强,然后利用理想气体状态方程列式即可求解.

练习册系列答案
相关题目
15. 由相关电磁学理论可以知道,若圆环形通电导线的中心为O,环的半径为R,环中通以电流为I,如图1所示,环心O处的磁感应强度大小B=$\frac{{μ}_{0}}{2}$$•\frac{I}{R}$,其中μ0为真空磁导率.若P点是过圆环形通电导线中心O点的轴线上的一点,且距O点的距离是x,如图2所示,有可能您不能直接求得P点处的磁感应强度B,但您能根据所学的物理知识判断出以下有关P点磁感应强度B的表达式是( )
由相关电磁学理论可以知道,若圆环形通电导线的中心为O,环的半径为R,环中通以电流为I,如图1所示,环心O处的磁感应强度大小B=$\frac{{μ}_{0}}{2}$$•\frac{I}{R}$,其中μ0为真空磁导率.若P点是过圆环形通电导线中心O点的轴线上的一点,且距O点的距离是x,如图2所示,有可能您不能直接求得P点处的磁感应强度B,但您能根据所学的物理知识判断出以下有关P点磁感应强度B的表达式是( )
 由相关电磁学理论可以知道,若圆环形通电导线的中心为O,环的半径为R,环中通以电流为I,如图1所示,环心O处的磁感应强度大小B=$\frac{{μ}_{0}}{2}$$•\frac{I}{R}$,其中μ0为真空磁导率.若P点是过圆环形通电导线中心O点的轴线上的一点,且距O点的距离是x,如图2所示,有可能您不能直接求得P点处的磁感应强度B,但您能根据所学的物理知识判断出以下有关P点磁感应强度B的表达式是( )
由相关电磁学理论可以知道,若圆环形通电导线的中心为O,环的半径为R,环中通以电流为I,如图1所示,环心O处的磁感应强度大小B=$\frac{{μ}_{0}}{2}$$•\frac{I}{R}$,其中μ0为真空磁导率.若P点是过圆环形通电导线中心O点的轴线上的一点,且距O点的距离是x,如图2所示,有可能您不能直接求得P点处的磁感应强度B,但您能根据所学的物理知识判断出以下有关P点磁感应强度B的表达式是( )| A. | BP=$\frac{{μ}_{0}}{2}$•$\frac{{R}^{2}I}{({R}^{2}+{x}^{2})^{\frac{3}{2}}}$ | B. | BP=$\frac{{μ}_{0}}{2}$•$\frac{{R}^{2}I}{({R}^{2}+{x}^{2})}$ | ||
| C. | BP=$\frac{{μ}_{0}}{2}$•$\frac{RI}{({R}^{2}+{x}^{2})^{\frac{3}{2}}}$ | D. | BP=$\frac{{μ}_{0}}{2}$•$\frac{{R}^{3}I}{({R}^{2}+{x}^{2})^{\frac{3}{2}}}$ |
9.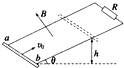 如图所示,间距为L米的光滑平等金属轨道上端用电阻R相连,其平面与水平面成θ角,整个装置处于磁感应强度为B匀强磁场中,磁场方向垂直轨道平面向上,质量为m,电阻为r的金属杆ab(长度略大于L),以初速度v0从轨道底端向上滑行,滑行到距底端高h的位置后又返回到底端,运动过程中,金属杆始终与导轨垂直且接触良好,不计金属轨道的电阻,已知重力加速度为g,则以下说法正确的是( )
如图所示,间距为L米的光滑平等金属轨道上端用电阻R相连,其平面与水平面成θ角,整个装置处于磁感应强度为B匀强磁场中,磁场方向垂直轨道平面向上,质量为m,电阻为r的金属杆ab(长度略大于L),以初速度v0从轨道底端向上滑行,滑行到距底端高h的位置后又返回到底端,运动过程中,金属杆始终与导轨垂直且接触良好,不计金属轨道的电阻,已知重力加速度为g,则以下说法正确的是( )
 如图所示,间距为L米的光滑平等金属轨道上端用电阻R相连,其平面与水平面成θ角,整个装置处于磁感应强度为B匀强磁场中,磁场方向垂直轨道平面向上,质量为m,电阻为r的金属杆ab(长度略大于L),以初速度v0从轨道底端向上滑行,滑行到距底端高h的位置后又返回到底端,运动过程中,金属杆始终与导轨垂直且接触良好,不计金属轨道的电阻,已知重力加速度为g,则以下说法正确的是( )
如图所示,间距为L米的光滑平等金属轨道上端用电阻R相连,其平面与水平面成θ角,整个装置处于磁感应强度为B匀强磁场中,磁场方向垂直轨道平面向上,质量为m,电阻为r的金属杆ab(长度略大于L),以初速度v0从轨道底端向上滑行,滑行到距底端高h的位置后又返回到底端,运动过程中,金属杆始终与导轨垂直且接触良好,不计金属轨道的电阻,已知重力加速度为g,则以下说法正确的是( )| A. | 杆ab先匀减速上滑,之后匀加速下滑,且上滑过程的加速度大于下滑过程的加速度 | |
| B. | 杆ab运动过程中安培力做功的功率等于电阻R的热功率 | |
| C. | 杆ab上滑过程中通过R的电荷量与下滑过程中通过R的电荷量相等 | |
| D. | 杆ab上滑到最高点的过程中电阻R上产生的焦耳热等于$\frac{R}{R+r}$($\frac{1}{2}$mv02-mgh) |
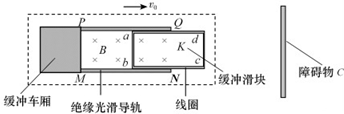
16.如图所示,虚线框内为某种电磁缓冲车的结构示意图,其主要部件为缓冲滑块K和质量为m的缓冲车厢,在缓冲车的底板上,沿车的轴线固定着两个光滑水平绝缘导轨PQ、MN,缓冲车的底部,安装电磁铁(图中未画出),能产生垂直于导轨平面的匀强磁场,磁场的磁感应强度大小为B.导轨内的缓冲滑块K由高强度绝缘材料制成,滑块K上绕有闭合矩形线圈abcd,线圈的总电阻为R,匝数为n,ab边长为L.假设缓冲车以速度v0与障碍物C碰撞后,滑块K立即停下,而缓冲车厢继续向前移动L后为零.已知缓冲车厢与障碍物和线圈的ab边均没有接触,不计一切摩擦阻力,在这个缓冲过程中,下列说法正确的是( )

| A. | 线圈中的感应电流沿逆时针方向(俯视),最大感应电流为$\frac{BL{v}_{0}}{R}$ | |
| B. | 线圈对电磁铁的作用力使缓冲车厢减速运动,从而实现缓冲 | |
| C. | 此过程中,线圈abcd产生的焦耳热为Q=$\frac{1}{2}$mv02 | |
| D. | 此过程中,通过线圈abcd的电荷量为q=$\frac{B{L}^{2}}{R}$ |
13.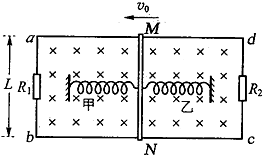 如图所示,abcd为固定的水平光滑矩形金属导轨,导轨间距为L,左右两端接有定值电阻R1和R2,R1=R2=R,整个装置处于磁感应强度大小为B、方向竖直向下的匀强磁场中.质量为m的导体棒MN放在导轨上,棒始终与导轨垂直且接触良好,不计导轨与棒的电阻.两根相同的轻质弹簧甲和乙一端固定,另一端同时与棒的中点连接.初始时刻,两根弹簧恰好处于原长状态,棒获得水平向左的初速度v0,第一次运动至最右端的过程中R1产生的电热为Q,下列说法中正确的是( )
如图所示,abcd为固定的水平光滑矩形金属导轨,导轨间距为L,左右两端接有定值电阻R1和R2,R1=R2=R,整个装置处于磁感应强度大小为B、方向竖直向下的匀强磁场中.质量为m的导体棒MN放在导轨上,棒始终与导轨垂直且接触良好,不计导轨与棒的电阻.两根相同的轻质弹簧甲和乙一端固定,另一端同时与棒的中点连接.初始时刻,两根弹簧恰好处于原长状态,棒获得水平向左的初速度v0,第一次运动至最右端的过程中R1产生的电热为Q,下列说法中正确的是( )
 如图所示,abcd为固定的水平光滑矩形金属导轨,导轨间距为L,左右两端接有定值电阻R1和R2,R1=R2=R,整个装置处于磁感应强度大小为B、方向竖直向下的匀强磁场中.质量为m的导体棒MN放在导轨上,棒始终与导轨垂直且接触良好,不计导轨与棒的电阻.两根相同的轻质弹簧甲和乙一端固定,另一端同时与棒的中点连接.初始时刻,两根弹簧恰好处于原长状态,棒获得水平向左的初速度v0,第一次运动至最右端的过程中R1产生的电热为Q,下列说法中正确的是( )
如图所示,abcd为固定的水平光滑矩形金属导轨,导轨间距为L,左右两端接有定值电阻R1和R2,R1=R2=R,整个装置处于磁感应强度大小为B、方向竖直向下的匀强磁场中.质量为m的导体棒MN放在导轨上,棒始终与导轨垂直且接触良好,不计导轨与棒的电阻.两根相同的轻质弹簧甲和乙一端固定,另一端同时与棒的中点连接.初始时刻,两根弹簧恰好处于原长状态,棒获得水平向左的初速度v0,第一次运动至最右端的过程中R1产生的电热为Q,下列说法中正确的是( )| A. | 初始时刻棒所受安培力的大小为$\frac{{B}^{2}{L}^{2}{v}_{0}}{R}$ | |
| B. | 棒第一次回到初始位置的时刻,R2的电功率为$\frac{{B}^{2}{L}^{2}{{v}_{0}}^{2}}{R}$ | |
| C. | 棒第一次到达最右端的时刻,两根弹簧具有弹性势能的总量为$\frac{1}{2}$mv${\;}_{0}^{2}$-Q | |
| D. | 从初始时刻至棒第一次到达最左端的过程中,整个回路产生的电热大于$\frac{2Q}{3}$ |
14. 如图所示,质量为m的物体用细绳牵引着在光滑的水平面上作匀速圆周运动.O为一光滑的孔,当拉力为F时,转动半径为R;当拉力增大到8F时,物体仍作匀速圆周运动,此时转动半径为$\frac{R}{2}$.在此过程中,拉力对物体做的功为( )
如图所示,质量为m的物体用细绳牵引着在光滑的水平面上作匀速圆周运动.O为一光滑的孔,当拉力为F时,转动半径为R;当拉力增大到8F时,物体仍作匀速圆周运动,此时转动半径为$\frac{R}{2}$.在此过程中,拉力对物体做的功为( )
 如图所示,质量为m的物体用细绳牵引着在光滑的水平面上作匀速圆周运动.O为一光滑的孔,当拉力为F时,转动半径为R;当拉力增大到8F时,物体仍作匀速圆周运动,此时转动半径为$\frac{R}{2}$.在此过程中,拉力对物体做的功为( )
如图所示,质量为m的物体用细绳牵引着在光滑的水平面上作匀速圆周运动.O为一光滑的孔,当拉力为F时,转动半径为R;当拉力增大到8F时,物体仍作匀速圆周运动,此时转动半径为$\frac{R}{2}$.在此过程中,拉力对物体做的功为( )| A. | $\frac{7}{2}$FR | B. | $\frac{7}{4}$FR | C. | $\frac{3}{2}$FR | D. | 4FR |

 如图所示,打点计时器固定在轨道上端,纸带穿过打点计时器与小车相连,平衡好摩擦力后接通电源,打点计时器工作,轻推小车使之匀速下滑(车轮不打滑),纸带上留下清晰的点迹.
如图所示,打点计时器固定在轨道上端,纸带穿过打点计时器与小车相连,平衡好摩擦力后接通电源,打点计时器工作,轻推小车使之匀速下滑(车轮不打滑),纸带上留下清晰的点迹.