题目内容
13.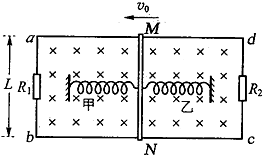 如图所示,abcd为固定的水平光滑矩形金属导轨,导轨间距为L,左右两端接有定值电阻R1和R2,R1=R2=R,整个装置处于磁感应强度大小为B、方向竖直向下的匀强磁场中.质量为m的导体棒MN放在导轨上,棒始终与导轨垂直且接触良好,不计导轨与棒的电阻.两根相同的轻质弹簧甲和乙一端固定,另一端同时与棒的中点连接.初始时刻,两根弹簧恰好处于原长状态,棒获得水平向左的初速度v0,第一次运动至最右端的过程中R1产生的电热为Q,下列说法中正确的是( )
如图所示,abcd为固定的水平光滑矩形金属导轨,导轨间距为L,左右两端接有定值电阻R1和R2,R1=R2=R,整个装置处于磁感应强度大小为B、方向竖直向下的匀强磁场中.质量为m的导体棒MN放在导轨上,棒始终与导轨垂直且接触良好,不计导轨与棒的电阻.两根相同的轻质弹簧甲和乙一端固定,另一端同时与棒的中点连接.初始时刻,两根弹簧恰好处于原长状态,棒获得水平向左的初速度v0,第一次运动至最右端的过程中R1产生的电热为Q,下列说法中正确的是( )| A. | 初始时刻棒所受安培力的大小为$\frac{{B}^{2}{L}^{2}{v}_{0}}{R}$ | |
| B. | 棒第一次回到初始位置的时刻,R2的电功率为$\frac{{B}^{2}{L}^{2}{{v}_{0}}^{2}}{R}$ | |
| C. | 棒第一次到达最右端的时刻,两根弹簧具有弹性势能的总量为$\frac{1}{2}$mv${\;}_{0}^{2}$-Q | |
| D. | 从初始时刻至棒第一次到达最左端的过程中,整个回路产生的电热大于$\frac{2Q}{3}$ |
分析 由E=BLv0、I=$\frac{E}{R}$、F=BIL三个公式结合求解初始时刻棒受到安培力大小.MN棒从开始到第一次运动至最右端,电阻R上产生的焦耳热为2Q,整个回路产生的焦耳热为4Q.
解答 解:A、由F=BIL及I=$\frac{BL{v}_{0}}{{R}_{并}}$=$\frac{BL{v}_{0}}{\frac{1}{2}R}$,得安培力大小为FA=BIL=$\frac{2{B}^{2}{{L}^{2}v}_{0}}{R}$.故A错误;
B、由于安培力始终对MN做负功,产生焦耳热,由动能定理得:当棒再次回到初始位置时,速度小于v0,棒产生的感应电动势小于BLv0,则AB间电阻R的功率小于$\frac{{B}^{2}{L}^{2}{v}_{0}^{2}}{R}$,故B错误;
C、由能量守恒得知,当棒第一次达到最右端时,物体的机械能全部转化为整个回路中的焦耳热和甲乙弹簧的弹性势能,两个电阻相同并联,故产生的热量相同,则电路中产生总热量为2Q,所以两根弹簧具有的弹性势能为$\frac{1}{2}$$m{v}_{0}^{2}-2Q$,故C错误;
D、由于安培力始终对MN做负功,产生焦耳热,棒第一次达到最左端的过程中,棒平均速度最大,安培力平均值最大,电路中产生总热量为2Q,从初始时刻至棒第一次到达最左端的过程中;整个回路中产生的焦耳热应大于$\frac{1}{3}$×2Q,故D正确.
故选:D
点评 本题分析系统中能量如何转化是难点,也是关键点,根据导体棒克服安培力做功等于产生的焦耳热,分析电阻R上产生的热量.

练习册系列答案
相关题目
3.在“描绘小灯泡的伏安特性曲线”实验中,要测量一个标有“3V 1.5W”的灯泡两端的电压和通过它的电流,现有如下器材:

A.直流电源3V(内阻可不计) B.直流电流表0~600mA(内阻约0.5Ω) C.直流电压表0~3V(内阻约3kΩ) D.滑动变阻器(10Ω,1A)E.滑动变阻器(1kΩ,300mA) F.开关、导线若干
(1)本实验中滑动变阻器选用D(填“D”或“E”)
(2)某同学用导线a、b、c、d、e、f、g和h连接的电路如图1所示,电路中所有元器件都是完好的,且电压表和电流表已调零.闭合开关后发现电压表的示数为2V,电流表的示数为零,小灯泡不亮,则可确定断路的导线是d;若电压表示数为零,电流表的示数为0.3A,小灯泡亮,则断路的导线是h;若反复调节滑动变阻器,小灯泡亮度发生变化,但电压表、电流表示数不能调为零,则断路的导线是g.
(3)表中的各组数据是该同学在实验中测得的,根据表格中的数据在如图3所示的方格纸上作出该灯泡的伏安特性曲线.
(4)如图2所示,将两个这样的灯泡并联后再与5Ω的定值电阻R0串联,接在电压恒定为4V的电路上,每个灯泡的实际功率为0.30 w(结果保留两位有效数字).

A.直流电源3V(内阻可不计) B.直流电流表0~600mA(内阻约0.5Ω) C.直流电压表0~3V(内阻约3kΩ) D.滑动变阻器(10Ω,1A)E.滑动变阻器(1kΩ,300mA) F.开关、导线若干
(1)本实验中滑动变阻器选用D(填“D”或“E”)
(2)某同学用导线a、b、c、d、e、f、g和h连接的电路如图1所示,电路中所有元器件都是完好的,且电压表和电流表已调零.闭合开关后发现电压表的示数为2V,电流表的示数为零,小灯泡不亮,则可确定断路的导线是d;若电压表示数为零,电流表的示数为0.3A,小灯泡亮,则断路的导线是h;若反复调节滑动变阻器,小灯泡亮度发生变化,但电压表、电流表示数不能调为零,则断路的导线是g.
(3)表中的各组数据是该同学在实验中测得的,根据表格中的数据在如图3所示的方格纸上作出该灯泡的伏安特性曲线.
| U/V | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
| I/A | 0 | 0.17 | 0.30 | 0.39 | 0.45 | 0.49 |
8.比值法定义物理量是物理学中一种常用的方法,下列物理量中属于用比值法定义的是( )
| A. | a=$\frac{F}{m}$ | B. | T=$\frac{2π}{ω}$ | C. | C=$\frac{Q}{U}$ | D. | I=$\frac{U}{R}$ |
18.下列叙述正确的有( )
| A. | 气体的压强越大,分子的平均动能越大 | |
| B. | 自然界中只要涉及热现象的实际过程都具有方向性 | |
| C. | 外界气体做正功,气体的内能一定增大 | |
| D. | 扩散现象与布朗运动都与温度有关 |
2. 如图所示,物体P用一根水平轻弹簧和竖直墙相连,放在粗糙水平面上,静止时弹簧的长度大于自然长度,用一个从零开始逐渐增大的水平力F向右作用在P上,直到把P拉动,在P被拉动之前的过程中,弹簧对P的弹力FN的大小和地面对P的摩擦力Ff的大小变化情况是( )
如图所示,物体P用一根水平轻弹簧和竖直墙相连,放在粗糙水平面上,静止时弹簧的长度大于自然长度,用一个从零开始逐渐增大的水平力F向右作用在P上,直到把P拉动,在P被拉动之前的过程中,弹簧对P的弹力FN的大小和地面对P的摩擦力Ff的大小变化情况是( )
 如图所示,物体P用一根水平轻弹簧和竖直墙相连,放在粗糙水平面上,静止时弹簧的长度大于自然长度,用一个从零开始逐渐增大的水平力F向右作用在P上,直到把P拉动,在P被拉动之前的过程中,弹簧对P的弹力FN的大小和地面对P的摩擦力Ff的大小变化情况是( )
如图所示,物体P用一根水平轻弹簧和竖直墙相连,放在粗糙水平面上,静止时弹簧的长度大于自然长度,用一个从零开始逐渐增大的水平力F向右作用在P上,直到把P拉动,在P被拉动之前的过程中,弹簧对P的弹力FN的大小和地面对P的摩擦力Ff的大小变化情况是( )| A. | FN保持不变,Ff始终减小 | B. | FN保持不变,Ff先减小后增大 | ||
| C. | FN先不变后增大,Ff先减小后增大 | D. | FN始终增大,Ff始终减小 |
3. 如图所示,水平地面上有一坑,其竖直截面为半圆,ab为沿水平方向的直径,O为球心,若在a点以某一初速度沿ab方向抛出一小球,小球击中坑壁,不计空气阻力,则( )
如图所示,水平地面上有一坑,其竖直截面为半圆,ab为沿水平方向的直径,O为球心,若在a点以某一初速度沿ab方向抛出一小球,小球击中坑壁,不计空气阻力,则( )
 如图所示,水平地面上有一坑,其竖直截面为半圆,ab为沿水平方向的直径,O为球心,若在a点以某一初速度沿ab方向抛出一小球,小球击中坑壁,不计空气阻力,则( )
如图所示,水平地面上有一坑,其竖直截面为半圆,ab为沿水平方向的直径,O为球心,若在a点以某一初速度沿ab方向抛出一小球,小球击中坑壁,不计空气阻力,则( )| A. | 小球的初速度越大,在坑中运动的时间一定越长 | |
| B. | 小球的初速度不同,在坑中的运动时间可能相同 | |
| C. | 小球与坑壁相撞时速度方向的反向延长线可能过O点 | |
| D. | 小球与坑壁相撞时速度方向的反向延长线不可能过O点 |
 “拔火罐”是一种中医疗法,为了探究“火罐”内的温度,某人设计了如图实验.圆柱状薄壁气缸(横截面积为S)被固定在铁架台上,轻质活塞通过细线与重物m相连,将一团燃烧的轻质酒精棉球从缸底的开关K处扔到气缸内,酒精棉球熄灭时密闭开关K,此时活塞下的细线刚好拉直且拉力为零,而这时活塞距缸底为L.由于气缸传热良好,随后重物会被吸起,最后重物稳定在距地面$\frac{L}{10}$处.已知环境温度为27℃不变,$\frac{mg}{s}$与$\frac{1}{6}$大气压强相当,气缸内的气体可看做理想气体,问酒精棉球熄灭时气缸内的温度为多少摄氏度?
“拔火罐”是一种中医疗法,为了探究“火罐”内的温度,某人设计了如图实验.圆柱状薄壁气缸(横截面积为S)被固定在铁架台上,轻质活塞通过细线与重物m相连,将一团燃烧的轻质酒精棉球从缸底的开关K处扔到气缸内,酒精棉球熄灭时密闭开关K,此时活塞下的细线刚好拉直且拉力为零,而这时活塞距缸底为L.由于气缸传热良好,随后重物会被吸起,最后重物稳定在距地面$\frac{L}{10}$处.已知环境温度为27℃不变,$\frac{mg}{s}$与$\frac{1}{6}$大气压强相当,气缸内的气体可看做理想气体,问酒精棉球熄灭时气缸内的温度为多少摄氏度?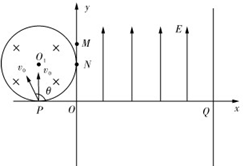 如图所示,在直角坐标系xOy的第一象限区域中,有沿y轴正方向的匀强电场,电场强度的大小为E=kv0,在第二象限内有一半径为R=b的圆形区域磁场,圆形磁场的圆心O1坐标为(-b,b),与坐标轴分别相切于P点和N点,磁场方向垂直纸面向里,在x=3b处垂直于x轴放置一平面荧光屏,与x轴交点为Q,大量的电子以相同的速率在纸面内从P点进入圆形磁场,电子的速度方向在与x轴正方向成θ角的范围内,其中沿y轴正方向的电子经过磁场到达N点,速度与x轴正方向成θ角的电子经过磁场到达M点且M点坐标为(0,1.5b),忽略电子间的相互作用力,不计电子的重力,电子的比荷为$\frac{e}{m}$=$\frac{{v}_{0}}{kb}$,求:
如图所示,在直角坐标系xOy的第一象限区域中,有沿y轴正方向的匀强电场,电场强度的大小为E=kv0,在第二象限内有一半径为R=b的圆形区域磁场,圆形磁场的圆心O1坐标为(-b,b),与坐标轴分别相切于P点和N点,磁场方向垂直纸面向里,在x=3b处垂直于x轴放置一平面荧光屏,与x轴交点为Q,大量的电子以相同的速率在纸面内从P点进入圆形磁场,电子的速度方向在与x轴正方向成θ角的范围内,其中沿y轴正方向的电子经过磁场到达N点,速度与x轴正方向成θ角的电子经过磁场到达M点且M点坐标为(0,1.5b),忽略电子间的相互作用力,不计电子的重力,电子的比荷为$\frac{e}{m}$=$\frac{{v}_{0}}{kb}$,求: