题目内容
10.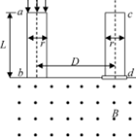 某两级串列加速器外形设计酷似“U”型,其主体结构简图如图所示,其中ab、cd为两底面为正方形的长方体加速管,加速管长为L,底面边长为r且两加速管底面有一边在一条线上.两加速管中心轴线的距离为D=49r,加速管内存在和轴线平行的匀强电场,b、d的下方区域存在垂直两加速管轴线平面的匀强磁场,磁感强度大小为B,现将速度很小的负一价粒子均匀地从a端面输入,经过加速管ab加速,垂直进入匀强磁场偏转,到达d处时,可被设在d处的特殊装置将其电子剥离(粒子速度不变,特殊装置大小可忽略),成为三价正粒子,沿轴线进入的粒子恰能沿两加速管轴线加速,已知b、d两端相等,a、c两端电势相等,元电荷为e,该粒子质量为m,不计粒子重力及粒子间相互作用力.
某两级串列加速器外形设计酷似“U”型,其主体结构简图如图所示,其中ab、cd为两底面为正方形的长方体加速管,加速管长为L,底面边长为r且两加速管底面有一边在一条线上.两加速管中心轴线的距离为D=49r,加速管内存在和轴线平行的匀强电场,b、d的下方区域存在垂直两加速管轴线平面的匀强磁场,磁感强度大小为B,现将速度很小的负一价粒子均匀地从a端面输入,经过加速管ab加速,垂直进入匀强磁场偏转,到达d处时,可被设在d处的特殊装置将其电子剥离(粒子速度不变,特殊装置大小可忽略),成为三价正粒子,沿轴线进入的粒子恰能沿两加速管轴线加速,已知b、d两端相等,a、c两端电势相等,元电荷为e,该粒子质量为m,不计粒子重力及粒子间相互作用力.(1)试求a、b两端的电势差Uab.
(2)仅改变加速管电压,则粒子在加速器中经历的最短时间是多少?
(3)实际工作时,磁场可能会与设计值B有一定偏差△B,而会以B-△B至B+△B间的某一确定值工作,若要求至少有90%的粒子能被成功加速,试求偏差△B的最大值.
分析 (1)加速电场中运用动能定理,在磁场中运用洛伦兹力提供向心力结合几何关系,即可求出a、b两端的电势差Uab;
(2)分别对两个加速管运用动能定理,根据两个加速管的电压相同,求出粒子速度关系,再求出粒子在加速管中运动的时间t1以及粒子在磁场中运动的时间t2加和即可,根据周期公式可知t2为半个周期,是一定值,t1越短,粒子运动的总时间也越短,在磁场中运动的半径最大,再根据洛伦兹力提供向心力,联立即可求出粒子在加速器中经历的最短时间;
(3)根据洛伦兹力提供向心力几何临界结合关系即可求出偏差△B的最大值.
解答 解:(1)沿轴线加速的粒子从b端进入磁场时速度为v,在磁场中运动的直径为D,则:
-eUab=$\frac{1}{2}m{v}^{2}$ ①
evB=$\frac{m{v}^{2}}{\frac{D}{2}}$ ②
联立①②两式可得:Uab=$-\frac{{D}^{2}e{B}^{2}}{8m}$
(2)在ab加速管中:-eUab′=$\frac{1}{2}m{v′}^{2}$ ③
在cd加速管中:-3eUcd′=$\frac{1}{2}mv{″}^{2}$-$\frac{1}{2}mv{′}^{2}$ ④
又Uab′=Ucd′⑤
由③④⑤式子可知:v″=2v′⑥
在加速管中总时间为t1=$\frac{L}{\frac{v′}{2}}$+$\frac{L}{\frac{v′+v″}{2}}$=$\frac{8L}{3v′}$ ⑦
粒子在磁场中运动的时间与速度无关:t2=$\frac{1}{2}T$=$\frac{1}{2}•\frac{2πm}{eB}$=$\frac{πm}{eB}$⑧
若在电场中时间最短,则粒子末速度最大,粒子以最大半径运动时速度最大,此时直径d=D+r
即:ev′B=$\frac{mv{′}^{2}}{\frac{D+r}{2}}$⑨
由⑥⑦⑧⑨式可得粒子在加速器中经历的最短时间:tmin=$[\frac{16L}{3(D+r)}+π]\frac{m}{eB}$=$[\frac{16L}{150r}+π]\frac{m}{eB}$
(3)按照设计要求工作时粒子在磁场中运动时,evB=m$\frac{{v}^{2}}{R}$⑩
且2R=D⑪
当磁场为B′时,R′=$\frac{mv}{eB′}$⑫
要求90%的粒子能实现加速
若磁场变弱,则:$\frac{2R′-D}{r}$<0.1⑬
联立⑩⑪⑫⑬式得:B′>$\frac{49}{50}$B
此时偏差△B=B-$\frac{49}{50}$B=$\frac{B}{50}$
若磁场变强,则:$\frac{D-2R′}{r}$<0.1⑭
联立⑩⑪⑫⑭式得:B′<$\frac{49}{48}$B
此时偏差△B=$\frac{49}{48}$B-B=$\frac{1}{48}$B
综上所述偏差△B的最大值:△Bmax=$\frac{B}{50}$
解:(1)a、b两端的电势差Uab为$-\frac{{D}^{2}e{B}^{2}}{8m}$;
(2)仅改变加速管电压,粒子在加速器中经历的最短时间为$[\frac{16L}{150r}+π]\frac{m}{eB}$;
(3)实际工作时,磁场可能会与设计值B有一定偏差△B,而会以B-△B至B+△B间的某一确定值工作,若要求至少有90%的粒子能被成功加速,偏差△B的最大值为$\frac{B}{50}$.
点评 本题考查带电粒子在复合场中的运动,解题关键是要读懂题,找出已知条件,清楚粒子运动的过程,选择合适的规律解题,第一问较为常规难度不大;第二问要注意分析时间最短的条件;第三问磁感应强度发生波动时,要注意有两种情况:变大或者变小,分别求两次的波动值,取两次波动值中的较大的即为偏差△B的最大值.

 发散思维新课堂系列答案
发散思维新课堂系列答案| A. | 质量一定相等 | B. | 动能一定相等 | ||
| C. | 动量一定相同 | D. | 以上说法都不正确 |
A.用天平测出小车A的质量为mA=0.4kg,小车B的质量为mB=0.2kg
B.更换纸带重复操作三次
C.小车A靠近打点计时器放置,在车后固定纸带,把小车B放在长木板中间
D.把长木板平放在桌面上,在一端固定打点计时器,连接电源
E.接通电源,并给小车A一定的初速度vA,小车A与小车B相撞黏合成一个整体
(1)请将以上步骤按操作的先后顺序排列出来ADCEB.
(2)打点计时器打下的纸带中,比较理想的一条如图所示,根据这些数据把下表空白处①②③④的数值补充完整.

| 碰撞前 | 碰撞后 | ||
| 物理量 | A车 | B车 | AB整体 |
| 质量(kg) | 0.4 | 0.2 | 0.6 |
| 速度(m/s) | 3.0 | 0 | ①2.0 |
| $\frac{v}{m}$ (m•s-1•kg-1) | 7.5 | 0 | ②3.3 |
| mv (kg•m/s) | 1.2 | 0 | ③1.2 |
| mv 2 (kg•m2/s2) | 3.6 | 0 | ④2.4 |
 一质量为m的物体与斜面间的动摩擦因数为μ,斜面倾角为θ,重力加速度为g.物体在斜面上运动轨迹如图所示,在图示时刻物体受到斜面摩擦力的大小为( )
一质量为m的物体与斜面间的动摩擦因数为μ,斜面倾角为θ,重力加速度为g.物体在斜面上运动轨迹如图所示,在图示时刻物体受到斜面摩擦力的大小为( )| A. | mgsinθ | B. | μmgsinθ | C. | μmgcosθ | D. | mgcosθ |
| A. | 波长变长 | B. | 速度变小 | C. | 光子能量变小 | D. | 频率变大 |
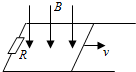 如图,两平行金属导轨位于同一水平面上,相距l,左端与一电阻R相连;整个系统置于匀强磁场中,磁感应强度大小为B,方向竖直向下.一质量为m的导体棒置于导轨上,在水平恒力F作用下沿导轨从静止开始向右滑动,当滑动位移为x时速度达到最大vm,滑动过程中始终保持与导轨垂直并接触良好,已知导体棒与导轨间的动摩擦因数为μ,重力加速度大小为g,导轨和导体棒的电阻均可忽略.求
如图,两平行金属导轨位于同一水平面上,相距l,左端与一电阻R相连;整个系统置于匀强磁场中,磁感应强度大小为B,方向竖直向下.一质量为m的导体棒置于导轨上,在水平恒力F作用下沿导轨从静止开始向右滑动,当滑动位移为x时速度达到最大vm,滑动过程中始终保持与导轨垂直并接触良好,已知导体棒与导轨间的动摩擦因数为μ,重力加速度大小为g,导轨和导体棒的电阻均可忽略.求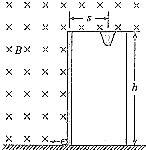 如图所示,水平地面上方有绝缘弹性竖直挡板,板高h=9m,与板等高处有一水平放置的篮筐,筐口的中心离挡板s=3m.板的左侧以及上端与筐口的连线上方存在匀强磁场和匀强电场,磁场方向垂直纸面向里,磁感应强度B=1T;质量m=1×10-3kg、电荷量q=-1×10-5C,可视为质点的带电小球从挡板最下端,以某一速度水平射入场中做匀速圆周运动,若与挡板相碰就以原速率弹回,且碰撞时间不计,碰撞时电荷量不变,小球最后都能从筐口的中心处落入筐中(不考虑与地面碰撞后反弹入筐情况),g=10m/s2,求:
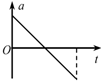
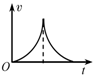
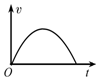
如图所示,水平地面上方有绝缘弹性竖直挡板,板高h=9m,与板等高处有一水平放置的篮筐,筐口的中心离挡板s=3m.板的左侧以及上端与筐口的连线上方存在匀强磁场和匀强电场,磁场方向垂直纸面向里,磁感应强度B=1T;质量m=1×10-3kg、电荷量q=-1×10-5C,可视为质点的带电小球从挡板最下端,以某一速度水平射入场中做匀速圆周运动,若与挡板相碰就以原速率弹回,且碰撞时间不计,碰撞时电荷量不变,小球最后都能从筐口的中心处落入筐中(不考虑与地面碰撞后反弹入筐情况),g=10m/s2,求: 如图,在竖直向下的匀强磁场中有两根竖直放置的平行粗糙导轨CD、EF,导轨上放有一金属棒MN.现从t=0时刻起,给棒通以图示方向的电流且电流强度与时间成正比,即I=kt,其中k为常量,金属棒与导轨始终垂直且接触良好.下列关于棒的速度v、加速度a随时间t变化的关系图象,可能正确的是( )
如图,在竖直向下的匀强磁场中有两根竖直放置的平行粗糙导轨CD、EF,导轨上放有一金属棒MN.现从t=0时刻起,给棒通以图示方向的电流且电流强度与时间成正比,即I=kt,其中k为常量,金属棒与导轨始终垂直且接触良好.下列关于棒的速度v、加速度a随时间t变化的关系图象,可能正确的是( )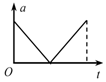
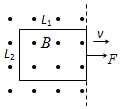 如图所示,长L1、宽L2、电阻为R的单匝矩形线圈放置在光滑绝缘的水平桌面上,匀强磁场的磁感应强度为B、方向竖直向上,线圈的右边框正好处于匀强磁场的边缘,线圈平面与磁感线垂直.现施加一水平向右的拉力使线圈以速度v匀速向右运动.
如图所示,长L1、宽L2、电阻为R的单匝矩形线圈放置在光滑绝缘的水平桌面上,匀强磁场的磁感应强度为B、方向竖直向上,线圈的右边框正好处于匀强磁场的边缘,线圈平面与磁感线垂直.现施加一水平向右的拉力使线圈以速度v匀速向右运动.