题目内容
5.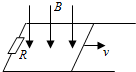 如图,两平行金属导轨位于同一水平面上,相距l,左端与一电阻R相连;整个系统置于匀强磁场中,磁感应强度大小为B,方向竖直向下.一质量为m的导体棒置于导轨上,在水平恒力F作用下沿导轨从静止开始向右滑动,当滑动位移为x时速度达到最大vm,滑动过程中始终保持与导轨垂直并接触良好,已知导体棒与导轨间的动摩擦因数为μ,重力加速度大小为g,导轨和导体棒的电阻均可忽略.求
如图,两平行金属导轨位于同一水平面上,相距l,左端与一电阻R相连;整个系统置于匀强磁场中,磁感应强度大小为B,方向竖直向下.一质量为m的导体棒置于导轨上,在水平恒力F作用下沿导轨从静止开始向右滑动,当滑动位移为x时速度达到最大vm,滑动过程中始终保持与导轨垂直并接触良好,已知导体棒与导轨间的动摩擦因数为μ,重力加速度大小为g,导轨和导体棒的电阻均可忽略.求(1)此过程中通过电阻R的电荷量q;
(2)此过程中电阻R产生的热量Q..
分析 (1)由导体棒运动过程的磁通量变化量,通过楞次定律求得平均电动势,进而得到平均电流,即可求电量;
(2)由稳定状态受力平衡求得最大速度,再根据能量守恒即可求得热量.
解答 解:(1)此过程中通过电阻R的电荷量$q=\overline{I}t=\frac{\overline{E}}{R}t=\frac{△Φ}{R}=\frac{Bl}{R}x$;
(2)导体棒达到最大速度时受力平衡,故有:$F=μmg+\frac{{B}^{2}{l}^{2}{v}_{m}}{R}$,那么,${v}_{m}=\frac{(F-μmg)R}{{B}^{2}{l}^{2}}$;
所以,由能量守恒定律可得:$Fx-fx-Q=\frac{1}{2}m{{v}_{m}}^{2}$;
所以,$Q=(F-μmg)x-\frac{1}{2}m{{v}_{m}}^{2}$=$(F-μmg)x-\frac{m(F-μmg)^{2}{R}^{2}}{2{B}^{4}{l}^{4}}$;
答:(1)此过程中通过电阻R的电荷量q为$\frac{Blx}{R}$;
(2)此过程中电阻R产生的热量Q为$(F-μmg)x-\frac{m(F-μmg)^{2}{R}^{2}}{2{B}^{4}{l}^{4}}$.
点评 在闭合电路切割磁感线的问题中,一般通过楞次定律由平均电动势求得平均电流进而得到电量;通过能量守恒定律求解焦耳热.

练习册系列答案
相关题目
16.对于经典力学和量子力学理论,下列说法正确的是( )
| A. | 经典力学能够解释微观粒子的运动规律 | |
| B. | 经典力学取得了巨大成就,但也有局限性 | |
| C. | 由于相对论与量子力学的提出,经典力学已不再适用了 | |
| D. | 经典力学适用于宏观物体的低速运动问题,不适用于微观粒子的高速运动问题 |
14.“天舟一号”货运飞船于2017年4月20日文昌航天发射中心成功发射升空,与“天宫二号”空间实验室对接前,“天舟一号”在距地面约380km的圆轨道上飞行,同步卫星的轨道高度为36000km,则“天舟一号”与同步卫星相比较,较小的物理量是( )
| A. | 角速度 | B. | 线速度 | C. | 周期 | D. | 向心加速度 |
17. 如图所示,一横截面为等腰直角三角形的玻璃棱镜,两种颜色不同的可见光细光束a、b,垂直于斜边从空气射向玻璃,光路如图所示,则下列说法正确的是( )
如图所示,一横截面为等腰直角三角形的玻璃棱镜,两种颜色不同的可见光细光束a、b,垂直于斜边从空气射向玻璃,光路如图所示,则下列说法正确的是( )
 如图所示,一横截面为等腰直角三角形的玻璃棱镜,两种颜色不同的可见光细光束a、b,垂直于斜边从空气射向玻璃,光路如图所示,则下列说法正确的是( )
如图所示,一横截面为等腰直角三角形的玻璃棱镜,两种颜色不同的可见光细光束a、b,垂直于斜边从空气射向玻璃,光路如图所示,则下列说法正确的是( )| A. | 玻璃对a光的折射率小于对b光的折射率 | |
| B. | a光和b光由空气进入玻璃棱镜后频率都变小 | |
| C. | a光和b光在玻璃中传播时a光的波长小于b光的波长 | |
| D. | 在相同条件下进行双缝干涉实验,a光的条纹间距比b光大 | |
| E. | a光和b光以相同的入射角由玻璃射向空气,若逐渐增大入射角,则b光先发生全反射 |
14. 光滑行金属导轨M、N水平放置,导轨间距为L,导轨上放置着一根与导轨垂直、长为L的导体棒PQ.导轨左端与由电容成的电路相连接,装置俯视如图所示.导轨所在的空间存在方向垂直于导轨平面胆E磁感应强度为B的匀强磁场.现给导体棒PQ一初速度v0使导体棒向右这动,当电路隐定后,导体棒U右做匀速运动.设导轨足够长导线及导体棒的电不计,则以下说正确的是( )
光滑行金属导轨M、N水平放置,导轨间距为L,导轨上放置着一根与导轨垂直、长为L的导体棒PQ.导轨左端与由电容成的电路相连接,装置俯视如图所示.导轨所在的空间存在方向垂直于导轨平面胆E磁感应强度为B的匀强磁场.现给导体棒PQ一初速度v0使导体棒向右这动,当电路隐定后,导体棒U右做匀速运动.设导轨足够长导线及导体棒的电不计,则以下说正确的是( )
 光滑行金属导轨M、N水平放置,导轨间距为L,导轨上放置着一根与导轨垂直、长为L的导体棒PQ.导轨左端与由电容成的电路相连接,装置俯视如图所示.导轨所在的空间存在方向垂直于导轨平面胆E磁感应强度为B的匀强磁场.现给导体棒PQ一初速度v0使导体棒向右这动,当电路隐定后,导体棒U右做匀速运动.设导轨足够长导线及导体棒的电不计,则以下说正确的是( )
光滑行金属导轨M、N水平放置,导轨间距为L,导轨上放置着一根与导轨垂直、长为L的导体棒PQ.导轨左端与由电容成的电路相连接,装置俯视如图所示.导轨所在的空间存在方向垂直于导轨平面胆E磁感应强度为B的匀强磁场.现给导体棒PQ一初速度v0使导体棒向右这动,当电路隐定后,导体棒U右做匀速运动.设导轨足够长导线及导体棒的电不计,则以下说正确的是( )| A. | v<v0 | |
| B. | 导体棒以初速度v0开始做匀减速运动,最后以速度v做匀速运动 | |
| C. | 当电路稳定后,电容器所带电荷量为零 | |
| D. | 当电路稳定后,电容器所带电荷量为CBLv |
15.一定质量的物体在恒定合外力作用下运动,则( )
| A. | 物体一定作匀变速直线运动 | B. | 物体的动能随时间均匀变化 | ||
| C. | 物体的机械能一定不守恒 | D. | 物体的动量随时间均匀变化 |
 如图所示,质量为M的木块静止在光滑的水平面上,轻弹簧左端与木块连接,右端固定在墙壁上.一质量为m的子弹以大小为v0的速度从左端射向木块,子弹未穿出木块(子弹与木块作用时间极短).求:弹簧被压缩至最短时具有的弹性势能.
如图所示,质量为M的木块静止在光滑的水平面上,轻弹簧左端与木块连接,右端固定在墙壁上.一质量为m的子弹以大小为v0的速度从左端射向木块,子弹未穿出木块(子弹与木块作用时间极短).求:弹簧被压缩至最短时具有的弹性势能. 如图所示,用绝缘支架固定的小球A带正电,带正电小球用丝线悬挂在B或C位置,丝线将向右(选填“左”、“右”)偏转,悬挂在B(选填“B”、“C”) 位置处的丝线与竖直方向的夹角较大.
如图所示,用绝缘支架固定的小球A带正电,带正电小球用丝线悬挂在B或C位置,丝线将向右(选填“左”、“右”)偏转,悬挂在B(选填“B”、“C”) 位置处的丝线与竖直方向的夹角较大.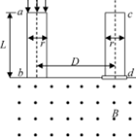 某两级串列加速器外形设计酷似“U”型,其主体结构简图如图所示,其中ab、cd为两底面为正方形的长方体加速管,加速管长为L,底面边长为r且两加速管底面有一边在一条线上.两加速管中心轴线的距离为D=49r,加速管内存在和轴线平行的匀强电场,b、d的下方区域存在垂直两加速管轴线平面的匀强磁场,磁感强度大小为B,现将速度很小的负一价粒子均匀地从a端面输入,经过加速管ab加速,垂直进入匀强磁场偏转,到达d处时,可被设在d处的特殊装置将其电子剥离(粒子速度不变,特殊装置大小可忽略),成为三价正粒子,沿轴线进入的粒子恰能沿两加速管轴线加速,已知b、d两端相等,a、c两端电势相等,元电荷为e,该粒子质量为m,不计粒子重力及粒子间相互作用力.
某两级串列加速器外形设计酷似“U”型,其主体结构简图如图所示,其中ab、cd为两底面为正方形的长方体加速管,加速管长为L,底面边长为r且两加速管底面有一边在一条线上.两加速管中心轴线的距离为D=49r,加速管内存在和轴线平行的匀强电场,b、d的下方区域存在垂直两加速管轴线平面的匀强磁场,磁感强度大小为B,现将速度很小的负一价粒子均匀地从a端面输入,经过加速管ab加速,垂直进入匀强磁场偏转,到达d处时,可被设在d处的特殊装置将其电子剥离(粒子速度不变,特殊装置大小可忽略),成为三价正粒子,沿轴线进入的粒子恰能沿两加速管轴线加速,已知b、d两端相等,a、c两端电势相等,元电荷为e,该粒子质量为m,不计粒子重力及粒子间相互作用力.