题目内容
16. .如图所示,已知绳长为L=50cm,水平杆L′=0.2m,小球质量m=0.8kg,整个装置可绕竖直轴转动,绳子与竖直方向成37°角(sin37°=0.6,cos37°=0.8),(g取10m/s2 )求
.如图所示,已知绳长为L=50cm,水平杆L′=0.2m,小球质量m=0.8kg,整个装置可绕竖直轴转动,绳子与竖直方向成37°角(sin37°=0.6,cos37°=0.8),(g取10m/s2 )求(1)绳子的张力为多少?
(2)该装置转动的角速度多大?
分析 (1)根据平行四边形定则求出绳子对小球的拉力.
(2)小球受重力和拉力,靠两个力的合力提供向心力,根据牛顿第二定律求出该装置的角速度.
解答  解:(1)小球受重力和拉力,靠两个力的合力提供向心力,在竖直方向上有:Fcos37°=mg,
解:(1)小球受重力和拉力,靠两个力的合力提供向心力,在竖直方向上有:Fcos37°=mg,
即为:F=$\frac{mg}{cos37°}=\frac{8}{0.8}N=10N$.
(2)r=L′+Lsin37°=0.2+0.5×0.6m=0.5m,
根据mgtan37°=mrω2得:$ω=\sqrt{\frac{gtan37°}{r}}=\sqrt{\frac{10×\frac{3}{4}}{0.5}}=\sqrt{15}rad/s$.
答:(1)绳子的张力为10N;
(2)该装置转动的角速度为$\sqrt{15}$rad/s.
点评 解决本题的关键知道小球做圆周运动向心力的来源,结合牛顿第二定律进行求解.

练习册系列答案
相关题目
1.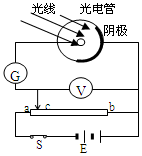 用如图所示的装置研究光电效应现象,所用光子能量为2.75eV光照射到光电管上时发生了光电效应,电流表G的示数不为零;移动变阻器的触点c,发现当电压表的示数大于或等于1.7V时,电流表示数为0,则下列说法正确的是( )
用如图所示的装置研究光电效应现象,所用光子能量为2.75eV光照射到光电管上时发生了光电效应,电流表G的示数不为零;移动变阻器的触点c,发现当电压表的示数大于或等于1.7V时,电流表示数为0,则下列说法正确的是( )
 用如图所示的装置研究光电效应现象,所用光子能量为2.75eV光照射到光电管上时发生了光电效应,电流表G的示数不为零;移动变阻器的触点c,发现当电压表的示数大于或等于1.7V时,电流表示数为0,则下列说法正确的是( )
用如图所示的装置研究光电效应现象,所用光子能量为2.75eV光照射到光电管上时发生了光电效应,电流表G的示数不为零;移动变阻器的触点c,发现当电压表的示数大于或等于1.7V时,电流表示数为0,则下列说法正确的是( )| A. | 光电子的最大初动能始终为1.05eV | |
| B. | 光电管阴极的逸出功为1.05eV | |
| C. | 电键S断开后,电流表G中有电流流过 | |
| D. | 改用能量为2.5eV的光子照射,移动变阻器的触点c,电流表G中也可能有电流 |
4.将能够产生匀强磁场的磁铁安装在火车首节车厢下面,如图(甲)(俯视图)所示,当它经过安放在两铁轨间的线圈时,线圈会产生一个电信号传输给控制中心,已知矩形线圈的长为L1,宽为L2,匝数n,若安装在火车车厢下南的磁铁产生的匀强磁场的宽度大于L2,当火车通过安放在铁轨之间的矩形线圈时,控制中心接收到的线圈两端的电压信号u随时间t变化的关系如图乙所示,不计线圈电阻,据此可知:火车的加速度;和安装在火车首节车厢下面的磁铁产生的匀强磁场宽度( )


| A. | $\frac{{u}_{2}-{u}_{1}}{nB{L}_{2}({t}_{2}-{t}_{1})}$ $\frac{{u}_{2}+{u}_{1}}{2nB{L}_{2}}$(t2-t1) | |
| B. | $\frac{{u}_{2}+{u}_{1}}{nB{L}_{2}({t}_{2}-{t}_{1})}$ $\frac{{u}_{2}+{u}_{1}}{2nB{L}_{2}}$(t2-t1) | |
| C. | $\frac{{u}_{2}+{u}_{1}}{nB{L}_{2}({t}_{2}-{t}_{1})}$ $\frac{{u}_{2}+{u}_{1}}{2nB{L}_{2}}$(t2-t1) | |
| D. | $\frac{{u}_{2}-{u}_{1}}{nB{L}_{2}({t}_{2}-{t}_{1})}$ $\frac{{u}_{2}+{u}_{1}}{2nB{L}_{2}}$(t2+t1) |
1.一质量为0.2kg的弹性小球,在光滑的水平面上以5m/s的速度垂直撞到墙上,碰撞后小球沿相反方向弹回,反弹后的速度大小与碰撞前的速度大小相等,则碰撞前后小球速度变化量的大小△v和碰撞过程中墙对小球所做的功W为( )
| A. | W=0,△v=10m/s | B. | W=5J,△v=10m/s | C. | W=5J,△v=0 | D. | W=0,△v=0m/s |
8.下列说法中正确的是( )
| A. | 发生α衰变时,新核与原来的原子核相比,中子数减少了2 | |
| B. | 用不可见光照射金属一定比用可见光照射同种金属产生的光电子的初动能大 | |
| C. | 由玻尔理论可知,氢原子辐射出一个光子后,其电势能减小,核外电子的动能增大,原子总能量不变 | |
| D. | 比结合能小的原子核结合成或分解成比结合能大的原子核时一定放出核能 |
5.一汽车在水平地面上以恒定功率P=20kw启动,所受的阻力大小是f=1000N,汽车启动后能达到的最大速度为( )
| A. | 40m/s | B. | 30 m/s | C. | 20 m/s | D. | 10 m/s |
6. 已知基态氢原子能量E1=-13.6eV,欲使处于基态的氢原子激发,下列 措施可行的是( )
已知基态氢原子能量E1=-13.6eV,欲使处于基态的氢原子激发,下列 措施可行的是( )
 已知基态氢原子能量E1=-13.6eV,欲使处于基态的氢原子激发,下列 措施可行的是( )
已知基态氢原子能量E1=-13.6eV,欲使处于基态的氢原子激发,下列 措施可行的是( )| A. | 用12eV的光子照射 | B. | 用12.09eV的光子照射 | ||
| C. | 用15eV的光子照射 | D. | 用12eV的电子碰撞 |
 如图所示,有一条两岸平行,河水均匀流动、流速恒定的大河,河水流速为2$\sqrt{3}$m/s,河宽为120m.某人驾着小船渡河,去程时船头朝向始终与河岸垂直,回程时行驶路线最短.已知去程的航线AB与岸边夹角为60°,且船在静水中的速率恒定不变.求:
如图所示,有一条两岸平行,河水均匀流动、流速恒定的大河,河水流速为2$\sqrt{3}$m/s,河宽为120m.某人驾着小船渡河,去程时船头朝向始终与河岸垂直,回程时行驶路线最短.已知去程的航线AB与岸边夹角为60°,且船在静水中的速率恒定不变.求: