题目内容
4. 一位同学的家住在一座25层的高楼内,他每天乘电梯上楼,随着所学物理知识的增多,有一天他突然想到,能否用所学物理知识较为准确地测出这座楼的高度呢?在以后的一段时间内他进行了多次实验测量,步骤如下:
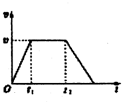
一位同学的家住在一座25层的高楼内,他每天乘电梯上楼,随着所学物理知识的增多,有一天他突然想到,能否用所学物理知识较为准确地测出这座楼的高度呢?在以后的一段时间内他进行了多次实验测量,步骤如下:经过多次仔细观察和反复测量,他发现电梯启动后的运动速度符合如图所示的规律,他就根据这一特点在电梯内用台秤、重物和停表测量这座楼房的高度.他将台秤放在电梯内,将重物放在台秤的托盘上,电梯从第一层开始启动,经过不间断的运行,最后停在最高层.在整个过程中,他记录了台秤中不同时间段内的示数,记录的数据如表所示.但由于0~3.0s段的时间太短,他没有来得及将台秤的示数记录下来,假设在每个时间段内台秤的示数都是稳定的,重力加速度g取10m/s2.
(1)电梯在0~3.0s时间段内台秤的示数应该是多少?
(2)根据测量的数据计算该楼房每一层的平均高度.
| 时间/s | 电梯启动前 | 0~3.0 | 3.0~13.0 | 13.0~19.0 | 19.0以后 |
| 台秤示数/kg | 5.0 | 5.0 | 4.6 | 5.0 |
分析 以物体为研究对象,静止时示数为其重力,加速时为超重:F-mg=ma,减速时为失重:mg-F=ma(F为示数)由此求解.
解答 解:(1)电梯启动前,台秤时数为5.0kg,则物体重力:G=50N,由于表中各段时间内台秤的示数恒定,所以在时间${t}_{1}^{\;}$(0~3.0s)内,物体做匀加速运动,在时间${t}_{2}^{\;}$(3.s~13.0s)内物体做匀速直线运动,在时间${t}_{3}^{\;}$(13.0s~19.0s)内物体做匀减速直线运动,19.0s末速度减为零.
在13.0s~19.0s内,物体所受的支持力为:${F}_{N3}^{\;}=46N$,根
据牛顿第二定律有:$mg-{F}_{N3}^{\;}=m{a}_{3}^{\;}$
得在时间${t}_{3}^{\;}$内物体的加速度为:${a}_{3}^{\;}=\frac{mg-{F}_{N3}^{\;}}{m}=0.8m/{s}_{\;}^{2}$
13.0s末物体的速度为:${v}_{2}^{\;}={a}_{3}^{\;}{t}_{3}^{\;}=4.8m/s$
而由于电梯在13.0s末的速度与3.0s末的速度相同,因此根据匀变速运动规律
物体在0~3.0s内的加速度为:${a}_{1}^{\;}=1.6m/{s}_{\;}^{2}$
根据牛顿第二定律有:${F}_{N1}^{\;}-mg=m{a}_{1}^{\;}$
代入数据解得:${F}_{N1}^{\;}=58N$,即台秤的示数为5.8kg
(2)0~3.0s内物体的位移为:${x}_{1}^{\;}=\frac{1}{2}{a}_{1}^{\;}{t}_{1}^{2}=\frac{1}{2}×1.6×{3}_{\;}^{2}=7.2m$
3.0s~13.0s内物体的位移为:${x}_{2}^{\;}={v}_{2}^{\;}{t}_{2}^{\;}=48m$
13.0s~19.0s内物体的位移为:${x}_{3}^{\;}=\frac{v}{2}{t}_{3}^{\;}=\frac{4.8}{2}×6=14.4m$
则电梯上升的总高度,实际为24层的总高度为:$x={x}_{1}^{\;}+{x}_{2}^{\;}+{x}_{3}^{\;}=69.6m$
平均每层楼高为:h=2.9m
答:(1)电梯在0~3.0s时间段内台秤的示数应该是5.8kg
(2)根据测量的数据计算该楼房每一层的平均高度是2.9m
点评 明确超重时示数增加,失重时示数小于重力,对于物体的重力不会发生变化,由牛顿第二定律列方程可求.

 如图所示,质量为M、倾角为θ的斜面体C静止于粗糙的水平面上,质量为mA和mB的A、B保持相对静止一起沿斜面下滑,B、C接触面光滑,则( )
如图所示,质量为M、倾角为θ的斜面体C静止于粗糙的水平面上,质量为mA和mB的A、B保持相对静止一起沿斜面下滑,B、C接触面光滑,则( )| A. | 地面对C没有摩擦力的作用 | |
| B. | 地面对C的支持力大小为(M+mA+mB)g | |
| C. | B对A的摩擦力方向水平向左,大小为mAgsinθcosθ | |
| D. | A对B的压力大小为mAg |
| A. | 伽利略提出力不是维持物体运动的原因;奥斯特发现电磁感应现象 | |
| B. | 牛顿总结出了万有引力定律,库仑通过扭秤测出了万有引力常量的数值 | |
| C. | 爱因斯坦提出“光子”理论,成功地对光电效应进行了解释 | |
| D. | 贝克勒尔发现了天然放射现象 |
 如图所示,把系在轻绳上的A、B两球从图示位置同时由静止释放,绳开始时拉直,不计空气阻力和悬点O处的摩擦,则在两球向左下摆动的过程中,下列说法正确的是( )
如图所示,把系在轻绳上的A、B两球从图示位置同时由静止释放,绳开始时拉直,不计空气阻力和悬点O处的摩擦,则在两球向左下摆动的过程中,下列说法正确的是( )| A. | 绳OA对A球做正功 | |
| B. | 绳AB对B球不做功 | |
| C. | 绳AB对B球做正功 | |
| D. | 由于绳AB对A球做负功,所以A、B两球组成的系统机械能减小 |
| A. | 静止的汽车没有惯性 | B. | 汽车起动加速过程,惯性越来越大 | ||
| C. | 汽车转弯过程,惯性变大 | D. | 汽车装满货物时比空车时惯性大 |
 如图所示,物块P、Q叠放在水平地面上,保持静止,则地面受到的弹力等于( )
如图所示,物块P、Q叠放在水平地面上,保持静止,则地面受到的弹力等于( )| A. | Q的重力 | B. | P对Q的压力 | ||
| C. | P、Q的重力之和 | D. | P的重力加上Q对地面的压力 |
 如图所示为赛车场的一个“梨形”赛道,所有直道和弯道都在同一水平面内,两个弯道分别为半径R=90m的大圆弧和r=40m的小圆弧,直道与弯道相切.切点分别为A、B、C、D.大、小圆弧圆心O、O'距离L=100m.一质量m=800kg的赛车沿弯道路线行驶时,路面对轮胎的最大径向静摩擦力是赛车重力的k=2.25倍,假设赛车在直道上做匀变速直线运动,在弯道上做匀速圆周运动.求在赛车不打滑,绕赛道一圈时间最短的情况下(发动机功率足够大,刹车性能良好,取g=10m/s2,π=3.14,$\sqrt{3}$=1.73).
如图所示为赛车场的一个“梨形”赛道,所有直道和弯道都在同一水平面内,两个弯道分别为半径R=90m的大圆弧和r=40m的小圆弧,直道与弯道相切.切点分别为A、B、C、D.大、小圆弧圆心O、O'距离L=100m.一质量m=800kg的赛车沿弯道路线行驶时,路面对轮胎的最大径向静摩擦力是赛车重力的k=2.25倍,假设赛车在直道上做匀变速直线运动,在弯道上做匀速圆周运动.求在赛车不打滑,绕赛道一圈时间最短的情况下(发动机功率足够大,刹车性能良好,取g=10m/s2,π=3.14,$\sqrt{3}$=1.73). 如图所示,用长为L的细线OA和水平细线将质量为m的小球系住,此时细线OA与竖直方向成θ=60°角.小球视为质点,重力加速度大小为g,不计空气阻力.烧断水平细线后,小球下摆,求:
如图所示,用长为L的细线OA和水平细线将质量为m的小球系住,此时细线OA与竖直方向成θ=60°角.小球视为质点,重力加速度大小为g,不计空气阻力.烧断水平细线后,小球下摆,求: