题目内容
16．
如图所示，用长为L的细线OA和水平细线将质量为m的小球系住，此时细线OA与竖直方向成θ=60°角．小球视为质点，重力加速度大小为g，不计空气阻力．烧断水平细线后，小球下摆，求：（1）小球经过最低点B时的速度大小
（2）小球经过最低点B时细线OA对小球的拉力大小．
分析 （1）小球下摆过程，只有重力做功，机械能守恒，根据动能定理或机械能守恒定律先列式求解出最低点的速度．
（2）在最低点，根据重力和拉力的合力提供向心力列式求解拉力．
解答 解：（1）小球由A到B过程中由动能定理得：
mgL（1-cosθ）=$\frac{1}{2}m{v}_{B}^{2}$
解得 vB=$\sqrt{gL}$
（2）在最低点B时，绳子的拉力F和重力mg的合力提供小球做圆周运动所需要的向心力，则：
F-mg=m$\frac{{v}_{B}^{2}}{L}$
解得 F=2mg
答：
（1）小球经过最低点B时的速度大小是$\sqrt{gL}$．
（2）小球经过最低点B时细线OA对小球的拉力大小是2mg．
点评 本题关键是对小球受力分析，知道小球运动的过程中机械能守恒，在最低点，由合力提供向心力．
练习册系列答案
相关题目
4．
一位同学的家住在一座25层的高楼内，他每天乘电梯上楼，随着所学物理知识的增多，有一天他突然想到，能否用所学物理知识较为准确地测出这座楼的高度呢？在以后的一段时间内他进行了多次实验测量，步骤如下：
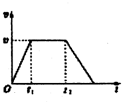
经过多次仔细观察和反复测量，他发现电梯启动后的运动速度符合如图所示的规律，他就根据这一特点在电梯内用台秤、重物和停表测量这座楼房的高度．他将台秤放在电梯内，将重物放在台秤的托盘上，电梯从第一层开始启动，经过不间断的运行，最后停在最高层．在整个过程中，他记录了台秤中不同时间段内的示数，记录的数据如表所示．但由于0～3.0s段的时间太短，他没有来得及将台秤的示数记录下来，假设在每个时间段内台秤的示数都是稳定的，重力加速度g取10m/s2．
（1）电梯在0～3.0s时间段内台秤的示数应该是多少？
（2）根据测量的数据计算该楼房每一层的平均高度．
一位同学的家住在一座25层的高楼内，他每天乘电梯上楼，随着所学物理知识的增多，有一天他突然想到，能否用所学物理知识较为准确地测出这座楼的高度呢？在以后的一段时间内他进行了多次实验测量，步骤如下：经过多次仔细观察和反复测量，他发现电梯启动后的运动速度符合如图所示的规律，他就根据这一特点在电梯内用台秤、重物和停表测量这座楼房的高度．他将台秤放在电梯内，将重物放在台秤的托盘上，电梯从第一层开始启动，经过不间断的运行，最后停在最高层．在整个过程中，他记录了台秤中不同时间段内的示数，记录的数据如表所示．但由于0～3.0s段的时间太短，他没有来得及将台秤的示数记录下来，假设在每个时间段内台秤的示数都是稳定的，重力加速度g取10m/s2．
（1）电梯在0～3.0s时间段内台秤的示数应该是多少？
（2）根据测量的数据计算该楼房每一层的平均高度．
| 时间/s | 电梯启动前 | 0～3.0 | 3.0～13.0 | 13.0～19.0 | 19.0以后 |
| 台秤示数/kg | 5.0 | 5.0 | 4.6 | 5.0 |
质量为10kg的物体在F=200N的水平推力作用下，从粗糙斜面的底端由静止开始沿斜面运动，斜面固定不动，与水平地面的夹角θ=37°，力F作用2s后撤去，物体在斜面上继续上滑了1.25s后，速度减为零．（已知sin 37°=0.6，cos 37°=0.8，g=10m/s2）．求：
如图所示，轨道ABCD的AB段为一半径R=0.2m的光滑圆形轨道，BC段为的竖直轨道，CD段为水平轨道．一质量为0.1kg的小球由A点从静止开始下滑到B点后离开B点做平抛运动（g取10m/s2），求：
如图，滑雪运动员从离水平地面30m的高处，以5m/s的初速度沿滑道自由向下滑行，阻力忽略不计．求运动员滑到水平地面时速度的大小．
如图所示，一物块质量m=2kg，放在水平面上，它与水平面的动摩擦因数μ=0.2，在水平拉力F作用下以加速度a=1 m/s2向右做匀加速直线运动（g取10 m/s2）．则运动中物块所受摩擦力大小f=4 N；物块所受的合力大小F合=2N；水平拉 力大小F=6N．
6．
如图所示，一条小船渡河，河水流速v1=3m/s，船在静水中速度v2=4m/s，船头方向与河岸垂直，关于小船的运动，下列说法正确的是（ ）
如图所示，一条小船渡河，河水流速v1=3m/s，船在静水中速度v2=4m/s，船头方向与河岸垂直，关于小船的运动，下列说法正确的是（ ）| A． | 小船的实际运动轨迹与岸垂直 | B． | 小船相对于岸的速度大小为1m/s | ||
| C． | 小船相对于岸的速度大小为5m/s | D． | 小船相对于岸的速度大小为7m/s |