题目内容
5. 如图所示,质量为M、倾角为θ的斜面体C静止于粗糙的水平面上,质量为mA和mB的A、B保持相对静止一起沿斜面下滑,B、C接触面光滑,则( )
如图所示,质量为M、倾角为θ的斜面体C静止于粗糙的水平面上,质量为mA和mB的A、B保持相对静止一起沿斜面下滑,B、C接触面光滑,则( )| A. | 地面对C没有摩擦力的作用 | |
| B. | 地面对C的支持力大小为(M+mA+mB)g | |
| C. | B对A的摩擦力方向水平向左,大小为mAgsinθcosθ | |
| D. | A对B的压力大小为mAg |
分析 对A、B、C整体受力分析,求出整体的加速度,再根据牛顿第二定律求地面对C的支持力和摩擦力;再隔离A受力分析,列出水平方向牛顿定律的分量式.
解答 解:A、B沿斜面向下的加速度a=gsinθ,水平方向ax=gsinθcosθ,${a_y}=g{sin^2}θ$,选整体分析,由于A、B有向左的加速度ax,地面对C的摩擦力方向向左,同理,地面对C的支持力小于(M+mA+mB)g,A、B错误.
CD、隔离A物体,F静A=mAax=mAgsinθcosθ,C正确.同理,B对A的支持力小于重力,所以A对B的压力小于mAg,D错误.
故选:C
点评 此题是牛顿第二定律的应用问题,解题时要分析物体的受力情况,将物体的加速度分解在水平和竖直方向,然后再这两个方向上建立牛顿方程;同时要正确选择研究对象,此题若分解力出现的方程将比较复杂,解方程较难.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
4.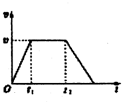 一位同学的家住在一座25层的高楼内,他每天乘电梯上楼,随着所学物理知识的增多,有一天他突然想到,能否用所学物理知识较为准确地测出这座楼的高度呢?在以后的一段时间内他进行了多次实验测量,步骤如下:
一位同学的家住在一座25层的高楼内,他每天乘电梯上楼,随着所学物理知识的增多,有一天他突然想到,能否用所学物理知识较为准确地测出这座楼的高度呢?在以后的一段时间内他进行了多次实验测量,步骤如下:
经过多次仔细观察和反复测量,他发现电梯启动后的运动速度符合如图所示的规律,他就根据这一特点在电梯内用台秤、重物和停表测量这座楼房的高度.他将台秤放在电梯内,将重物放在台秤的托盘上,电梯从第一层开始启动,经过不间断的运行,最后停在最高层.在整个过程中,他记录了台秤中不同时间段内的示数,记录的数据如表所示.但由于0~3.0s段的时间太短,他没有来得及将台秤的示数记录下来,假设在每个时间段内台秤的示数都是稳定的,重力加速度g取10m/s2.
(1)电梯在0~3.0s时间段内台秤的示数应该是多少?
(2)根据测量的数据计算该楼房每一层的平均高度.
 一位同学的家住在一座25层的高楼内,他每天乘电梯上楼,随着所学物理知识的增多,有一天他突然想到,能否用所学物理知识较为准确地测出这座楼的高度呢?在以后的一段时间内他进行了多次实验测量,步骤如下:
一位同学的家住在一座25层的高楼内,他每天乘电梯上楼,随着所学物理知识的增多,有一天他突然想到,能否用所学物理知识较为准确地测出这座楼的高度呢?在以后的一段时间内他进行了多次实验测量,步骤如下:经过多次仔细观察和反复测量,他发现电梯启动后的运动速度符合如图所示的规律,他就根据这一特点在电梯内用台秤、重物和停表测量这座楼房的高度.他将台秤放在电梯内,将重物放在台秤的托盘上,电梯从第一层开始启动,经过不间断的运行,最后停在最高层.在整个过程中,他记录了台秤中不同时间段内的示数,记录的数据如表所示.但由于0~3.0s段的时间太短,他没有来得及将台秤的示数记录下来,假设在每个时间段内台秤的示数都是稳定的,重力加速度g取10m/s2.
(1)电梯在0~3.0s时间段内台秤的示数应该是多少?
(2)根据测量的数据计算该楼房每一层的平均高度.
| 时间/s | 电梯启动前 | 0~3.0 | 3.0~13.0 | 13.0~19.0 | 19.0以后 |
| 台秤示数/kg | 5.0 | 5.0 | 4.6 | 5.0 |
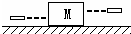 质量为M的均匀木块静止在光滑水平面上,木块左右两侧各有一位拿着完全相同步枪和子弹的射击手.首先左侧射手开枪,子弹水平射入木块的最大深度为d1,然后右侧射手开枪,子弹水平射入木块的最大深度为d2,如图设子弹均未射穿木块,子弹质量为m(M=2m)且两颗子弹与木块之间的作用力大小均相同.,求:当两颗子弹均相对木块静止时d1与 d2的比值.
质量为M的均匀木块静止在光滑水平面上,木块左右两侧各有一位拿着完全相同步枪和子弹的射击手.首先左侧射手开枪,子弹水平射入木块的最大深度为d1,然后右侧射手开枪,子弹水平射入木块的最大深度为d2,如图设子弹均未射穿木块,子弹质量为m(M=2m)且两颗子弹与木块之间的作用力大小均相同.,求:当两颗子弹均相对木块静止时d1与 d2的比值.
 光滑活塞封闭气缸内一定体积的气体,气缸静止在水平面上.已知活塞的质量为m、横截面积为s,气缸的质量为M,被封闭气体的高度为h1.然后用力(大小未知)缓慢向上提拉活塞,气缸刚离开地面时气体的高度为h2.已知重力加速度为g,不考虑被封闭气体的质量,求当地的大气压强.
光滑活塞封闭气缸内一定体积的气体,气缸静止在水平面上.已知活塞的质量为m、横截面积为s,气缸的质量为M,被封闭气体的高度为h1.然后用力(大小未知)缓慢向上提拉活塞,气缸刚离开地面时气体的高度为h2.已知重力加速度为g,不考虑被封闭气体的质量,求当地的大气压强. 如图所示,一物块质量m=2kg,放在水平面上,它与水平面的动摩擦因数μ=0.2,在水平拉力F作用下以加速度a=1 m/s2向右做匀加速直线运动(g取10 m/s2).则运动中物块所受摩擦力大小f=4 N;物块所受的合力大小F合=2N;水平拉 力大小F=6N.
如图所示,一物块质量m=2kg,放在水平面上,它与水平面的动摩擦因数μ=0.2,在水平拉力F作用下以加速度a=1 m/s2向右做匀加速直线运动(g取10 m/s2).则运动中物块所受摩擦力大小f=4 N;物块所受的合力大小F合=2N;水平拉 力大小F=6N.