题目内容
4. 如图所示,固定在竖直面内的圆弧轨道半径为R=2m,最高点A与圆心O等高,圆弧AB所对的圆心角θ=127°,圆弧在最低点与水平面相切.质量为m=0.5kg的小球从A点无初速释放后,从B点离开圆弧,沿圆弧在B点的切线方向斜抛出去的瞬时速率为vB=4m/s.抛出后小球运动轨迹的最高点为C,落地点为D.不计空气阻力,以水平面为重力势能的参考平面,取g=10m/s2.求:
如图所示,固定在竖直面内的圆弧轨道半径为R=2m,最高点A与圆心O等高,圆弧AB所对的圆心角θ=127°,圆弧在最低点与水平面相切.质量为m=0.5kg的小球从A点无初速释放后,从B点离开圆弧,沿圆弧在B点的切线方向斜抛出去的瞬时速率为vB=4m/s.抛出后小球运动轨迹的最高点为C,落地点为D.不计空气阻力,以水平面为重力势能的参考平面,取g=10m/s2.求:(1)小球沿A圆弧运动过程中克服摩擦阻力做的功Wf;
(2)小球到达轨迹最高点C时的速度大小vC;
(3)小球落地时的动能Ek.
分析 (1)从A到B的过程中,根据动能定理即可求解;
(2)从B到C做斜抛运动,水平方向做匀速直线运动,到达C点时,竖直方向速度为零,所以C点速度等于B点水平方向速度,根据几何关系求解;
(3)从B到D的过程中,根据动能定理求解.
解答 解:(1)从A到B的过程中,根据动能定理得:
$\frac{1}{2}m{{v}_{B}}^{2}-0=mgRcos(127°-90°)-{W}_{f}$
解得:Wf=4J
(2)从B到C做斜抛运动,水平方向做匀速直线运动,到达C点时,竖直方向速度为零,
所以C点速度等于B点水平方向速度,即vC=vBcos(127°-90°)=4×0.8=3.2m/s
(3)从B到D的过程中,根据动能定理得:
${E}_{K}-\frac{1}{2}m{v}^{2}=mg[R-Rcos(127°-90°)]$
解得:EK=6J
答:(1)小球沿A圆弧运动过程中克服摩擦阻力做的功Wf为4J;
(2)小球到达轨迹最高点C时的速度大小vC为3.2m/s;
(3)小球落地时的动能Ek为6J.
点评 本题主要考查了动能定理的直接应用,应用动能定理时要选择好研究对象和研究过程,这样会使问题简单化,同时注意几何关系在解题时的应用,难度适中.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
14. 电影《智取威虎山》中有精彩而又刺激的解放军战士滑雪的镜头.假设某战士从弧形的雪坡上沿水平方向飞出后,又落回到倾斜的雪坡上,如图所示,若倾斜的雪坡倾角为θ,战士飞出时的水平速度大小为v0,且他飞出后在空中的姿势保持不变,不计空气阻力,重力加速度为g,则( )
电影《智取威虎山》中有精彩而又刺激的解放军战士滑雪的镜头.假设某战士从弧形的雪坡上沿水平方向飞出后,又落回到倾斜的雪坡上,如图所示,若倾斜的雪坡倾角为θ,战士飞出时的水平速度大小为v0,且他飞出后在空中的姿势保持不变,不计空气阻力,重力加速度为g,则( )
 电影《智取威虎山》中有精彩而又刺激的解放军战士滑雪的镜头.假设某战士从弧形的雪坡上沿水平方向飞出后,又落回到倾斜的雪坡上,如图所示,若倾斜的雪坡倾角为θ,战士飞出时的水平速度大小为v0,且他飞出后在空中的姿势保持不变,不计空气阻力,重力加速度为g,则( )
电影《智取威虎山》中有精彩而又刺激的解放军战士滑雪的镜头.假设某战士从弧形的雪坡上沿水平方向飞出后,又落回到倾斜的雪坡上,如图所示,若倾斜的雪坡倾角为θ,战士飞出时的水平速度大小为v0,且他飞出后在空中的姿势保持不变,不计空气阻力,重力加速度为g,则( )| A. | 如果v0不同,该战士落到雪坡时的位置不同,速度方向相同 | |
| B. | 如果v0不同,该战士落到雪坡时的位置不同,但空中运动时间相同 | |
| C. | 该战士刚要落到雪坡上时的速度大小是$\frac{{v}_{0}}{cosθ}$ | |
| D. | 该战士在空中经历的时间是$\frac{{v}_{0}tanθ}{g}$ |
12.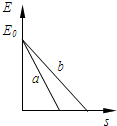 水平面上的甲、乙两物体,在某时刻动能相同,它们仅在摩擦力作用下逐渐停下来,图中,a、b分别表示甲、乙的动能E和位移s的图象,下列说法正确的是( )
水平面上的甲、乙两物体,在某时刻动能相同,它们仅在摩擦力作用下逐渐停下来,图中,a、b分别表示甲、乙的动能E和位移s的图象,下列说法正确的是( )
 水平面上的甲、乙两物体,在某时刻动能相同,它们仅在摩擦力作用下逐渐停下来,图中,a、b分别表示甲、乙的动能E和位移s的图象,下列说法正确的是( )
水平面上的甲、乙两物体,在某时刻动能相同,它们仅在摩擦力作用下逐渐停下来,图中,a、b分别表示甲、乙的动能E和位移s的图象,下列说法正确的是( )| A. | 若甲和乙与水平面的动摩擦因数相同,则甲的质量一定比乙大 | |
| B. | 若甲和乙与水平面的动摩擦因数相同,则甲的初速度一定比乙大 | |
| C. | 若甲和乙的质量相等,则甲的运动时间一定比乙长 | |
| D. | 若甲和乙的质量相等,则甲和地面的动摩擦因数一定比乙小 |
9.下列所述的实例中(均不计空气阻力),机械能守恒的是( )
| A. | 小石块被竖直向上抛出后在空中运动的过程 | |
| B. | 木箱沿粗糙斜面匀速下滑的过程 | |
| C. | 人乘电梯匀速上升的过程 | |
| D. | 子弹射穿木块的过程 |
16. 一列简谐波沿x轴传播,t=0时刻的波形如图,介质P回到平衡位置的最短时间0.1s,介质Q回到平衡位置的最短时间0.5s,此时两质点相对平衡位置位移相同,则( )
一列简谐波沿x轴传播,t=0时刻的波形如图,介质P回到平衡位置的最短时间0.1s,介质Q回到平衡位置的最短时间0.5s,此时两质点相对平衡位置位移相同,则( )
 一列简谐波沿x轴传播,t=0时刻的波形如图,介质P回到平衡位置的最短时间0.1s,介质Q回到平衡位置的最短时间0.5s,此时两质点相对平衡位置位移相同,则( )
一列简谐波沿x轴传播,t=0时刻的波形如图,介质P回到平衡位置的最短时间0.1s,介质Q回到平衡位置的最短时间0.5s,此时两质点相对平衡位置位移相同,则( )| A. | 该简谐波的传播周期为1.2s | |
| B. | 该简谐波的传播速度为0.1m/s | |
| C. | t=0.4s时P质点的加速度为负向最大 | |
| D. | 再经过1s,质点Q向右移动了0.1m |
16.一个物体沿直线运动,描绘出物体的$\frac{x}{t}$-t图象如图所示,则下列判断正确的是( )


| A. | 物体做匀速直线运动 | B. | 物体做变加速直线运动 | ||
| C. | 物体的初速度大小为-1m/s | D. | 物体的加速度大小为1m/s2 |
 如图所示,一架装载救援物资的飞机,在距水平地面h=500m的高处以v=100m/s的水平速度飞行,不计空气阻力,g取10m/s2.
如图所示,一架装载救援物资的飞机,在距水平地面h=500m的高处以v=100m/s的水平速度飞行,不计空气阻力,g取10m/s2. 在青少年科技创新大赛中,某同学展示了其设计的程序控制电动赛车,如图所示.赛车A质量M=2.0kg,长L=2m,高h=0.8m,额定功率P=36W.在赛车的最左端放一质量m=1.0kg的物体B(可视为质点),距赛车右端s=3.0m的地方固定另一个长方体物体C,它的高度为赛车高的$\frac{3}{4}$,宽度为赛车长的$\frac{1}{5}$.已知赛车A与物体B间的动摩擦因数μ=0.4,地面给赛车的阻力恒为地面支持力的k倍,k=0.2,通电后赛车A与物体B一起由静止向C运动,与C发生碰撞后赛车立即停止;赛车停止运动后,物体B在赛车上向右滑动,并从右端水平飞出,恰好越过C落到地面上.取g=10m/s2,不计空气阻力.求:
在青少年科技创新大赛中,某同学展示了其设计的程序控制电动赛车,如图所示.赛车A质量M=2.0kg,长L=2m,高h=0.8m,额定功率P=36W.在赛车的最左端放一质量m=1.0kg的物体B(可视为质点),距赛车右端s=3.0m的地方固定另一个长方体物体C,它的高度为赛车高的$\frac{3}{4}$,宽度为赛车长的$\frac{1}{5}$.已知赛车A与物体B间的动摩擦因数μ=0.4,地面给赛车的阻力恒为地面支持力的k倍,k=0.2,通电后赛车A与物体B一起由静止向C运动,与C发生碰撞后赛车立即停止;赛车停止运动后,物体B在赛车上向右滑动,并从右端水平飞出,恰好越过C落到地面上.取g=10m/s2,不计空气阻力.求: