题目内容
10.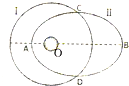 如图所示,曲线Ⅰ是绕地球做圆周运动卫星1的轨道示意图,其半径为R;曲线Ⅱ是绕地球做椭圆运动卫星2的轨道的示意图,O点为地球球心,AB为椭圆的长轴,两轨道和地心都在同一平面内,己知在两轨道上运动的卫星的周期相等,万有引力常量为G,地球质量为M,下列说法正确的是( )
如图所示,曲线Ⅰ是绕地球做圆周运动卫星1的轨道示意图,其半径为R;曲线Ⅱ是绕地球做椭圆运动卫星2的轨道的示意图,O点为地球球心,AB为椭圆的长轴,两轨道和地心都在同一平面内,己知在两轨道上运动的卫星的周期相等,万有引力常量为G,地球质量为M,下列说法正确的是( )| A. | 椭圆轨道的长轴AB长度为R | |
| B. | 若OA=0.5R,则卫星在B点的速率vB<$\sqrt{\frac{2GM}{3R}}$ | |
| C. | 在Ⅰ轨道上卫星1的速率为v0,在Ⅱ轨道的卫星2在B点的速率为vB,则v0<vB | |
| D. | 两颗卫星运动到C点时,卫星1和卫星2的加速度不同 |
分析 根据开普勒定律比较长轴与R的关系,根据万有引力的大小,通过牛顿第二定律比较加速度,结合速度的大小比较向心加速度的大小.
解答 解:A、根据开普勒第三定律得$\frac{{a}^{3}}{{T}^{2}}$=k,a为半长轴,己知卫星在两轨道上运动的卫星的周期相等,所以椭圆轨道的长轴长度为2R,故A错误;
B、若OA=0.5R,则OB=1.5R,
人造卫星绕地球做匀速圆周运动,根据万有引力提供向心力,
$\frac{GMm}{{r}^{2}}=m\frac{{v}^{2}}{r}$,
如果卫星以OB为轨道半径做匀速圆周运动,v=$\sqrt{\frac{2GM}{3R}}$,
在Ⅱ轨道上,卫星在B点要减速,做近心运动,所以卫星在B点的速率vB<$\sqrt{\frac{2GM}{3R}}$,故B正确.
C、B点为椭圆轨道的远地点,速度比较小,v0表示做匀速圆周运动的速度,v0>vB.故C错误;
D、由于两卫星离地高度相同,故两卫星受到的万有引力产生的加速度相同,故D错误;
故选:B.
点评 本题考查万有引力定律、开普勒第三定律、牛顿第二定律等知识,知道卫星变轨的原理是解决本题的关键.

练习册系列答案
相关题目
20.下列说法中正确的是( )
| A. | 布朗运动就是液中大量分子的无规则运动 | |
| B. | 布朗运动的剧烈程度与温度无关 | |
| C. | 固体很难被压缩,说明固体内分子之间只有相互的斥力 | |
| D. | 物体的温度越高,分子热运动越剧烈 |
18.下列叙述正确的有( )
| A. | 气体的压强越大,分子的平均动能越大 | |
| B. | 自然界中只要涉及热现象的实际过程都具有方向性 | |
| C. | 外界气体做正功,气体的内能一定增大 | |
| D. | 扩散现象与布朗运动都与温度有关 |
2. 如图所示,物体P用一根水平轻弹簧和竖直墙相连,放在粗糙水平面上,静止时弹簧的长度大于自然长度,用一个从零开始逐渐增大的水平力F向右作用在P上,直到把P拉动,在P被拉动之前的过程中,弹簧对P的弹力FN的大小和地面对P的摩擦力Ff的大小变化情况是( )
如图所示,物体P用一根水平轻弹簧和竖直墙相连,放在粗糙水平面上,静止时弹簧的长度大于自然长度,用一个从零开始逐渐增大的水平力F向右作用在P上,直到把P拉动,在P被拉动之前的过程中,弹簧对P的弹力FN的大小和地面对P的摩擦力Ff的大小变化情况是( )
 如图所示,物体P用一根水平轻弹簧和竖直墙相连,放在粗糙水平面上,静止时弹簧的长度大于自然长度,用一个从零开始逐渐增大的水平力F向右作用在P上,直到把P拉动,在P被拉动之前的过程中,弹簧对P的弹力FN的大小和地面对P的摩擦力Ff的大小变化情况是( )
如图所示,物体P用一根水平轻弹簧和竖直墙相连,放在粗糙水平面上,静止时弹簧的长度大于自然长度,用一个从零开始逐渐增大的水平力F向右作用在P上,直到把P拉动,在P被拉动之前的过程中,弹簧对P的弹力FN的大小和地面对P的摩擦力Ff的大小变化情况是( )| A. | FN保持不变,Ff始终减小 | B. | FN保持不变,Ff先减小后增大 | ||
| C. | FN先不变后增大,Ff先减小后增大 | D. | FN始终增大,Ff始终减小 |
19. 如图所示,水平面上的物体受水平向右、大小为F的拉力作用,物体处于静止状态.如果改用大小仍为F、水平向左的力推物体,则( )
如图所示,水平面上的物体受水平向右、大小为F的拉力作用,物体处于静止状态.如果改用大小仍为F、水平向左的力推物体,则( )
 如图所示,水平面上的物体受水平向右、大小为F的拉力作用,物体处于静止状态.如果改用大小仍为F、水平向左的力推物体,则( )
如图所示,水平面上的物体受水平向右、大小为F的拉力作用,物体处于静止状态.如果改用大小仍为F、水平向左的力推物体,则( )| A. | 物体处于静止状态,受到的摩擦力大小不变 | |
| B. | 物体处于静止状态,受到的摩擦力变小 | |
| C. | 物体沿水平面滑动,受到的摩擦力大小不变 | |
| D. | 物体沼水平面滑动,受到的摩擦力变小 |
20. 如图所示,实现为沿x轴传播的一列简谐横波在t=0时刻的波形图,质点P恰好在平衡位置,虚线是这列波在t=0.2s时刻的波形图.已知该波的波速是0.8m/s,那么,则下列说法中正确的是( )
如图所示,实现为沿x轴传播的一列简谐横波在t=0时刻的波形图,质点P恰好在平衡位置,虚线是这列波在t=0.2s时刻的波形图.已知该波的波速是0.8m/s,那么,则下列说法中正确的是( )
 如图所示,实现为沿x轴传播的一列简谐横波在t=0时刻的波形图,质点P恰好在平衡位置,虚线是这列波在t=0.2s时刻的波形图.已知该波的波速是0.8m/s,那么,则下列说法中正确的是( )
如图所示,实现为沿x轴传播的一列简谐横波在t=0时刻的波形图,质点P恰好在平衡位置,虚线是这列波在t=0.2s时刻的波形图.已知该波的波速是0.8m/s,那么,则下列说法中正确的是( )| A. | 这列波可能是沿x轴正方向传播的 | |
| B. | 在t=0时,x=4cm处的质点P的速度沿y轴负方向 | |
| C. | 质点P在0.6s时间内经过的路程为0.48m | |
| D. | 质点P在t=0.31s时刻速度方向与加速度方向相同 |
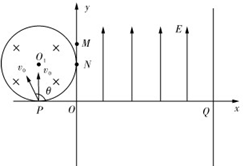 如图所示,在直角坐标系xOy的第一象限区域中,有沿y轴正方向的匀强电场,电场强度的大小为E=kv0,在第二象限内有一半径为R=b的圆形区域磁场,圆形磁场的圆心O1坐标为(-b,b),与坐标轴分别相切于P点和N点,磁场方向垂直纸面向里,在x=3b处垂直于x轴放置一平面荧光屏,与x轴交点为Q,大量的电子以相同的速率在纸面内从P点进入圆形磁场,电子的速度方向在与x轴正方向成θ角的范围内,其中沿y轴正方向的电子经过磁场到达N点,速度与x轴正方向成θ角的电子经过磁场到达M点且M点坐标为(0,1.5b),忽略电子间的相互作用力,不计电子的重力,电子的比荷为$\frac{e}{m}$=$\frac{{v}_{0}}{kb}$,求:
如图所示,在直角坐标系xOy的第一象限区域中,有沿y轴正方向的匀强电场,电场强度的大小为E=kv0,在第二象限内有一半径为R=b的圆形区域磁场,圆形磁场的圆心O1坐标为(-b,b),与坐标轴分别相切于P点和N点,磁场方向垂直纸面向里,在x=3b处垂直于x轴放置一平面荧光屏,与x轴交点为Q,大量的电子以相同的速率在纸面内从P点进入圆形磁场,电子的速度方向在与x轴正方向成θ角的范围内,其中沿y轴正方向的电子经过磁场到达N点,速度与x轴正方向成θ角的电子经过磁场到达M点且M点坐标为(0,1.5b),忽略电子间的相互作用力,不计电子的重力,电子的比荷为$\frac{e}{m}$=$\frac{{v}_{0}}{kb}$,求:
