题目内容
1．一质量为4×103kg的汽车，在平直公路上以60kw的恒定功率运动，经过50s，速度由20m/s增大到最大速度30m/s，则这段时间内汽车通过的位移为（ ）| A． | 500m | B． | 1000m | C． | 1500m | D． | 2000m |
分析 当汽车速度达到最大时，牵引力等于阻力，结合P=fvm，根据动能定理，抓住功率不变，求出这段时间内汽车的位移．
解答 解：汽车达到最大速度时，F=f，则${v}_{m}=\frac{P}{f}$，
根据动能定理有：Pt-fx=$\frac{1}{2}m{{v}_{m}}^{2}$$-\frac{1}{2}m{{v}_{0}}^{2}$，
代入数据联立解得x=1000m．
故选：B．
点评 解决本题的关键知道汽车以恒定功率启动做变加速运动，不能通过动力学知识求解位移，只能抓住功率不变，结合动能定理进行求解，知道速度最大时，牵引力等于阻力．
练习册系列答案
相关题目
11．小球由地面竖直上抛，上升的最大高度为H，地面为零势能面，在上升至离地高度h处，小球的势能是动能的2倍，空气阻力不计，则h等于（ ）
| A． | $\frac{H}{4}$ | B． | $\frac{H}{3}$ | C． | $\frac{H}{2}$ | D． | $\frac{2H}{3}$ |
12．
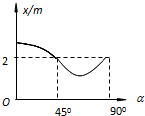某研究性学习小组为了测量木块与木板间的动摩擦因数，让木块以一定的初速度v0沿倾角可在0～90°任意调整的木板向上滑行，测出木块沿木板向上所能达到的最大位移x，画出木块向上所能达到的最大位移x与对应木板倾角α的图象，如图所示，由该图可求得木块与木板间的动摩擦因数为（g取10m/s2）（ ）
某研究性学习小组为了测量木块与木板间的动摩擦因数，让木块以一定的初速度v0沿倾角可在0～90°任意调整的木板向上滑行，测出木块沿木板向上所能达到的最大位移x，画出木块向上所能达到的最大位移x与对应木板倾角α的图象，如图所示，由该图可求得木块与木板间的动摩擦因数为（g取10m/s2）（ ）| A． | $\sqrt{2}$-1 | B． | 2-$\sqrt{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{3}}}{3}$ |
9．甲、乙两个质点同时、同地向同一方向做直线运动，它们的v-t图象如图所示，则由图象可知（ ）
| A． | 甲质点比乙质点运动的快，故乙追不上甲 | |
| B． | 在4s末时乙追上甲 | |
| C． | 在4s末时甲、乙的位移相同 | |
| D． | 甲做匀速直线运动，乙做初速度为零的匀加速直线运动 |
16．下列物理量不可能为负值的是（ ）
| A． | 加速度 | B． | 功 | C． | 动能 | D． | 重力势能 |
6．
如图所示，两个小球用长度不等的细线悬挂在天花板上的同一点，并在同一水平面内做匀速圆周运动，则下列说法正确的是（ ）
如图所示，两个小球用长度不等的细线悬挂在天花板上的同一点，并在同一水平面内做匀速圆周运动，则下列说法正确的是（ ）| A． | 两球运动的周期一定相同 | |
| B． | 两球运动的线速度大小一定相等 | |
| C． | 两球运动的角速度大小一定相等 | |
| D． | 两球运动的向心加速度大小一定相等 |
如图所示，第二象限的某个矩形区域内，有方向垂直于纸面向里磁感应强度为B1的匀强磁场，该磁场的下边界与x轴重合；第三象限内有互相正交的匀强电场和匀强磁场，两者场强分别E1=500V/m和B2=0.5T；第四象限有一电场强度E=2000$\sqrt{3}$V/m的匀强电场，方向与x轴负方向成600指向y轴负方向．一质量m=1×l0-14kg、电荷量q=1×10-10C的带正电的粒子以某一速度v从y轴上的N点沿与y轴负方向成60°角方向射入第二象限，后经P点进入第三象限内并沿直线运动，经过一段时间后，粒子经y轴上的M点与y轴负方向成60°角的方向进入第四象限，M点坐标（0，-0.1m），N点坐标（0，0.3m），粒子重力忽略不计．求：
在研究平抛运动的实验中，用一张印有小方格的纸记录小球的运动轨迹，小方格的边长L=1.6cm，取重力加速度g=10m/s2，若小球在平抛运动轨迹中的几个位置如图中的a、b、c、d所示，则小球平抛运动的初速度的计算式为v0=2$\sqrt{gL}$（用L、g表示），其值是0.80m/s（保留两位有效数字）．