题目内容
3．
如图所示，一轻质弹簧上端固定在O点，下端与一轻质活塞相连，活塞的横街面积S=50cm2，质量m=5kg的柱型气缸内被活塞封闭了一定质量的理想气体．若逐渐降低气体温度，当温度T1=360K时，气缸对地面恰好没有压力．已知气缸导热性能良好，不计活塞与汽缸壁之间的摩擦，设大气压p压=1×102Pa，g取10m/s2．（1）若弹簧的劲度系数k=500N/m，当气体温度升高到T2=500K时，弹簧处于自然状态，求此时活塞离气缸底部的距离；
（2）当降低气体温度为某一数值时，发现气缸离开地面上升了5cm，求此时气体的温度．
分析 （1）当温度为T1=360K时，气缸对地面恰好没有压力，根据胡克定律此时弹簧伸长量，当气体温度升高到T2=500K时，弹簧处于自然状态，设此时活塞离气缸底部的距离为l，根据体积公式求出体积得表达式，再根据理想气体状态方程求解即可；
（2）根据盖•吕萨克定律列式求解即可．
解答 解：（1）当温度为T1=360K时，气缸对地面恰好没有压力，此时弹簧伸长量x=$\frac{mg}{k}=0.1m$，
气体压强${P}_{1}={P}_{0}-\frac{mg}{S}=9×1{0}^{4}Pa$，
当气体温度升高到T2=500K时，弹簧处于自然状态，设此时活塞离气缸底部的距离为l，
则温度为T1=360K时，气体体积为V1=（l-x）S，
当气体温度升高到T2=500K时，气体体积V1=lS，压强${P}_{2}={P}_{0}=1×1{0}^{5}Pa$，
根据理想气体状态方程得：$\frac{{P}_{1}{V}_{1}}{{T}_{1}}$=$\frac{{P}_{2}{V}_{2}}{{T}_{2}}$
解得：l=0.5m，
（2）若缓慢降温至T3，气缸离开地面上升h=5cm时，压强P3=P1，体积V3=（l-x-h）S，
根据盖•吕萨克定律得：$\frac{{V}_{1}}{{T}_{1}}=\frac{{V}_{3}}{{T}_{3}}$
解得：T3=315K
答：（1）若弹簧的劲度系数k=500N/m，当气体温度升高到T2=500K时，弹簧处于自然状态，此时活塞离气缸底部的距离为0.5m；
（2）当降低气体温度为某一数值时，发现气缸离开地面上升了5cm，此时气体的温度为315K．
点评 本题主要考查理想气体状态方程的直接应用，特别注意公式中的温度应该用热力学温度，知道有活塞时，要根据平衡条件求解气体的压强，难度适中．
| A． | $\frac{gR{p}^{2}}{G{p}^{3}}$ | B． | $\frac{g{R}^{2}{q}^{3}}{G{p}^{2}}$ | C． | $\frac{gR{q}^{2}}{G{p}^{3}}$ | D． | $\frac{g{R}^{2}{p}^{3}}{G{q}^{2}}$ |
如图所示，用力F把铁块压在竖直墙上，此时重力为G的物体沿墙壁匀速下滑，若物体与墙壁之间的动摩擦因数为μ，则物体所受摩擦力的大小等于μF或等于G．
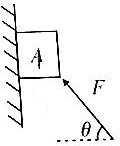如图所示，物体A的质量为m，受到推力F的作用，靠在光滑的竖直墙上，物体保持静止，则下列说法正确的是（ ）| A． | 物体A受到4个力作用 | B． | mg=Fcosθ | ||
| C． | 物体A对墙的压力为Fcosθ | D． | 撤去F后，物体A做自由落体运动 |
如图所示，粗心均匀的圆玻璃管两端封闭且竖直放置，玻璃管中的理想气体被一不导热的活塞分成两部分．当两部分气体温度均为T1=400K时，玻璃管下方气体的压强为上方气体压强的2倍，上方气体的体积是下方气体体积的2倍．为使上、下两部分气体的体积相等，保持上方气体温度不变，仅加热下方的气体，求下方气体的温度．| A． | 位移、时间、速度、加速度 | B． | 质量、路程、速率、速度 | ||
| C． | 平均速度、位移、加速度、力 | D． | 位移、路程、加速度、速率 |
| A． | $\frac{{v}_{A}}{{v}_{B}}=\frac{R}{R-d}\sqrt{\frac{R}{R+d}}$ | B． | $\frac{{v}_{A}}{{v}_{B}}=\frac{R}{R+d}\sqrt{\frac{R}{R-d}}$ | C． | $\frac{{v}_{A}}{{v}_{B}}=\frac{R+d}{R-d}$ | D． | $\frac{{v}_{A}}{{v}_{B}}=\sqrt{\frac{R-d}{R+d}}$ |
某同学为了探究质量均匀分布的直杆转动时的转动惯量，设计了如图所示的实验：