题目内容
16. 如图所示,长l=0.5m的轻质细杆,一端固定有一个质量为m=3kg的小球,另一端由电动机带动,使杆绕O点在竖直平面内做匀速圆周运动,小球的速率为v=2m/s.取g=10m/s2,
如图所示,长l=0.5m的轻质细杆,一端固定有一个质量为m=3kg的小球,另一端由电动机带动,使杆绕O点在竖直平面内做匀速圆周运动,小球的速率为v=2m/s.取g=10m/s2,(1)小球通过最高点时,对杆的拉力大小是多少?
(2)小球通过最低点时,对杆的拉力大小是多少?
分析 (1)在最高点,小球靠重力和杆的作用力的合力提供向心力,结合牛顿第二定律求出作用力的大小和方向.
(2)在最低点,小球靠重力和杆的拉力提供向心力,结合牛顿第二定律求出拉力的大小.
解答 解:(1)设小球在最高点时受杆的弹力向上,
则mg-FN=m$\frac{{v}^{2}}{l}$,得FN=mg-m$\frac{{v}^{2}}{l}$=$30-3×\frac{4}{0.5}$=6 N,
可知杆对小球的力向上,则小球对杆表现为压力,大小为6N.
(2)小球通过最低点时,根据牛顿第二定律得,F-mg=m$\frac{{v}^{2}}{l}$,
解得FN=mg+m$\frac{{v}^{2}}{l}$=$30+3×\frac{4}{0.5}$=54 N,
根据牛顿第三定律知,小球对杆的拉力为54N.
答:(1)小球通过最高点时,对杆的拉力大小是6N;
(2)小球通过最低点时,对杆的拉力大小是54N.
点评 解决本题的关键知道小球在最高点和最低点向心力的来源,结合牛顿第二定律进行求解,难度不大.

练习册系列答案
相关题目
5. 伽利略为了研究自由落体的规律,将落体实验转化为著名的“斜面实验”,对于这个研究过程,下列说法正确的是( )
伽利略为了研究自由落体的规律,将落体实验转化为著名的“斜面实验”,对于这个研究过程,下列说法正确的是( )
 伽利略为了研究自由落体的规律,将落体实验转化为著名的“斜面实验”,对于这个研究过程,下列说法正确的是( )
伽利略为了研究自由落体的规律,将落体实验转化为著名的“斜面实验”,对于这个研究过程,下列说法正确的是( )| A. | 斜面实验是一个用来研究V与t成正比的猜想是否正确 | |
| B. | 斜面实验放大了重力的作用,便于测量小球运动的路程 | |
| C. | 通过对斜面实验的观察与计算,直接得到落体运动的规律 | |
| D. | 不直接做落体实验是因为当时时间测量不够精确 |
7.某课题小组通过实验测量河水的电阻率.现备有一根均匀的长玻璃管(两端各有一个可移动圆形电极,可装入样品水,接触电阻不计)、直尺、待测的水样品.电路器材如表一,他们用伏安法多次测量的数据如表二(为实验处理的方便,实验时每次都把电流表示数调到相同);实验中还用10分度的游标卡尺测量了玻璃管的内径,结果如图甲所示.
表一
表二
(1)玻离管内径d的测量值为2.26 cm.
(2)根据表一器材和表二数据确定测量电路中电流表应该内接(填“内接”或“外接”),电路的连接方式应该采用分压电路(填“分压电路”或“限流电路”).
(3)用计算出的水柱长度L与水柱电阻R在图乙中描点,画出R-L图象(要求标出坐标轴的物理量、单位和对应的数值).
(4)计算出所测水的电阻率为1.06×102Ω•m.

表一
| 器材编号 | 器材名称 | 规格 |
| 1 | 电流表 | 200 μA,内阻约10Ω |
| 2 | 电压表 | 12V,内阻约100kΩ |
| 3 | 电池组 | 12V,内阻不计 |
| 4[ | 滑动变阻器 | 10Ω,1A |
| 5 | 开关 | |
| 6 | 导线 | 若干 |
| 7 | 定值电阻 | 100Ω |
| 序号 | 水柱长度/cm | 电压表示数/V | 电流表示数/μA |
| 1 | 10 | 2 | 100 |
| 2 | 20 | 4 | 100 |
| 3 | 30 | 6 | 100 |
| 4 | 40 | 8 | 100 |
| 5 | 50 | 10 | 100 |
(2)根据表一器材和表二数据确定测量电路中电流表应该内接(填“内接”或“外接”),电路的连接方式应该采用分压电路(填“分压电路”或“限流电路”).
(3)用计算出的水柱长度L与水柱电阻R在图乙中描点,画出R-L图象(要求标出坐标轴的物理量、单位和对应的数值).
(4)计算出所测水的电阻率为1.06×102Ω•m.

1.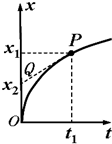 如图所示是一做匀变速直线运动的质点的位置-时间图象(x-t图象),P(t1,x1)为图象上一点.PQ为过P点的切线,与x轴交于点Q.则下列说法正确的是( )
如图所示是一做匀变速直线运动的质点的位置-时间图象(x-t图象),P(t1,x1)为图象上一点.PQ为过P点的切线,与x轴交于点Q.则下列说法正确的是( )
 如图所示是一做匀变速直线运动的质点的位置-时间图象(x-t图象),P(t1,x1)为图象上一点.PQ为过P点的切线,与x轴交于点Q.则下列说法正确的是( )
如图所示是一做匀变速直线运动的质点的位置-时间图象(x-t图象),P(t1,x1)为图象上一点.PQ为过P点的切线,与x轴交于点Q.则下列说法正确的是( )| A. | t1时刻,质点的速率为$\frac{{x}_{1}}{{t}_{1}}$ | |
| B. | t1时刻,质点的速率为$\frac{{x}_{1}-{x}_{2}}{{t}_{1}}$ | |
| C. | 质点的加速度大小为$\frac{{x}_{1}-{x}_{2}}{{t}_{1}^{2}}$ | |
| D. | 0-t1时间内,质点的平均速度大小为$\frac{2({x}_{1}-{x}_{2})}{{t}_{1}}$ |
6.在“研究平行板电容器的电容与哪些因素有关”的实验中,用电容表可以直接测量出该平行板电容器的电容大小.某同学在测量中,记录了一些测量结果,参看表,表中的数据是测量出的电容大小.在实验误差的允许范围内,可以得到的最直接的结论是( )
| 实验次数 | 极板材质 | 介质材料 | 正对面积 | |||
| S | $\frac{3}{4}s$ | $\frac{1}{2}s$ | $\frac{1}{4}s$ | |||
| ① | 铜 | 橡胶 | 680pF | 530pF | 380pF | 230pF |
| ② | 铁 | 橡胶 | 660pF | 520pF | 380pF | 240pF |
| ③ | 铝 | 亚克力板 | 330pF | 280pF | 230pF | 160pF |
| A. | 通过①和②数据,可知极板材料不影响平行板电容器的电容 | |
| B. | 通过①和③数据,可知极板材料和介质材料都影响平行板电容器的电容 | |
| C. | 通过②和③数据,可知介质材料影响平行板电容器的电容 | |
| D. | 通过①、②和③数据,可知极板的不同正对面积影响平行板电容器的电容 |
 如图,匀强电场中的点A、B、C、D、E、F、G、H为立方体的8个顶点.已知G、F、B、D点的电势分别为5V、1V、2V、4V,则A点的电势为( )
如图,匀强电场中的点A、B、C、D、E、F、G、H为立方体的8个顶点.已知G、F、B、D点的电势分别为5V、1V、2V、4V,则A点的电势为( )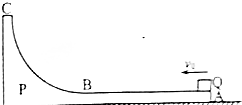 如图所示,质量为M=2kg的滑块P静止在光滑水平地面上,滑片P的AB段水平且粗糙,BC段为半径R=0.2m的光滑$\frac{1}{4}$弧面,AB部分的长度L=2m,一质量为m=1kg的小滑块Q以v0=6m/s的速度从A端滑入P,恰能滑到最高点C处,由C处返回后,最终停在AB之间的某一位置、取g=10m/s2,求;
如图所示,质量为M=2kg的滑块P静止在光滑水平地面上,滑片P的AB段水平且粗糙,BC段为半径R=0.2m的光滑$\frac{1}{4}$弧面,AB部分的长度L=2m,一质量为m=1kg的小滑块Q以v0=6m/s的速度从A端滑入P,恰能滑到最高点C处,由C处返回后,最终停在AB之间的某一位置、取g=10m/s2,求; 如图是半径为R的$\frac{1}{4}$圆弧,在圆弧上放置一光滑木板AB,一质量为m的木块由A端静止下滑,经B点(无机械能损失)滑向粗糙的水平面,运动s后在C点停下,已知木块与水平面间的动摩擦因数为μ,求木块由A运动到C点,重力mg的平均功率.
如图是半径为R的$\frac{1}{4}$圆弧,在圆弧上放置一光滑木板AB,一质量为m的木块由A端静止下滑,经B点(无机械能损失)滑向粗糙的水平面,运动s后在C点停下,已知木块与水平面间的动摩擦因数为μ,求木块由A运动到C点,重力mg的平均功率.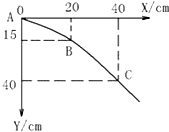 在做“研究平抛物体的运动”实验时
在做“研究平抛物体的运动”实验时