题目内容
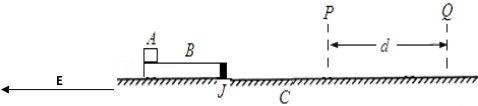
16. 如图所示,平行光滑导轨放在匀强磁场B中,B=0.4T,金属棒ab始终以恒定的速度v沿导轨向左匀速运动,导轨宽L=1m,电阻R1=R3=8Ω,R2=2Ω,导轨电阻不计,一电容器的极板水平放置,板间距离为d=10mm,内部有一个质量m=10-14kg,电量q=10-15C的微粒,在电键K断开时处于静止状态;当K闭合时,微粒以a=7m/s2的加速度匀加速下落,g=10m/s2,求:
如图所示,平行光滑导轨放在匀强磁场B中,B=0.4T,金属棒ab始终以恒定的速度v沿导轨向左匀速运动,导轨宽L=1m,电阻R1=R3=8Ω,R2=2Ω,导轨电阻不计,一电容器的极板水平放置,板间距离为d=10mm,内部有一个质量m=10-14kg,电量q=10-15C的微粒,在电键K断开时处于静止状态;当K闭合时,微粒以a=7m/s2的加速度匀加速下落,g=10m/s2,求:(1)金属棒ab的电动势和内电阻.
(2)金属棒ab运动速度的大小.
(3)K闭合后外力做功的功率.
分析 (1)K断开时,带电微粒在重力与电场力作用下处于静止状态,由平衡条件列出方程;K闭合时,粒子在重力和电场力作用下产生加速度,可求平行板间电压,根据闭合电路欧姆定律和串并联电路特点可求电动势和内电阻.
(2)由公式E=BLv求金属棒ab的速度.
(3)K闭合后,作用于棒的拉力的功率可以使用公式P=Fv求得.
解答 解:(1)K断开时,带电微粒在电容器两极间静止时,受到向上的电场力和向下的重力作用而平衡,则有
mg=$\frac{q{U}_{1}}{d}$
由此式可解出电容器两极板间的电压为:U1=$\frac{mgd}{q}$=$\frac{1{0}^{-14}×10×0.01}{1{0}^{-15}}$V=1V
由于K断开,R1、R2的电压和等于电容器两端电压U1,R3上无电流通过,可知电路中的感应电流即为通过R1、R2的电流I1,
I1=$\frac{{U}_{1}}{{R}_{2}+{R}_{1}}$=$\frac{1}{2+8}$A=0.1A,
从而ab切割磁感线运动产生的感应电动势为:
E=U1+I1r=1+0.1r…①
K闭合时,带电微粒向下做匀加速运动,由牛顿第二定律可得:
mg-$\frac{q{U}_{2}}{d}$=ma
得:U2=0.3V,此时的感应电流为 I2=$\frac{{U}_{2}}{{R}_{2}}$=$\frac{0.3}{2}$A=0.15A,
由闭合电路欧姆定律可得:E=I2($\frac{{R}_{1}{R}_{3}}{{R}_{1}+{R}_{3}}$+R2+r)=0.15(6+r)…②
解①②两式可得:E=1.2V,r=2Ω
(2)由E=BLv可得:v=$\frac{E}{BL}$=$\frac{1.2}{0.4×1}$m/s=3m/s,即导体棒ab匀速运动的速度v=3m/s
(3)K闭合时,通过ab的电流I2=0.15A,ab所受的安培力为 F2=BI2L=0.4×0.15×1N=0.06N
ab以速度v=3m/s做匀速运动,所受外力F必与磁场力F2大小相等、方向相反,即F=0.06N,方向向右.
可见,外力的功率为:P=Fv=0.06×3W=0.18W
答:
(1)金属棒ab的电动势是1.2V,内电阻是2Ω.
(2)金属棒ab运动速度的大小是3m/s.
(3)K闭合后外力做功的功率是0.18W.
点评 本题是电磁感应与电路的综合,它们联系的桥梁是电动势和电压,求电动势和内阻的方法与电路中的求解方法一样,对两种情况列出方程,组成方程组求解电动势和内阻.

 阅读快车系列答案
阅读快车系列答案 如图所示,实线为某吸尘板产生的电场线示意图,虚线为带负电灰尘的运动轨迹图,若带电灰尘是从A点运动到B,灰尘所受的电场力分别为FA、FB,电势分别为ϕA、ϕB,电势能分别为EA、EB,运动速度分别为vA、vB,则( )
如图所示,实线为某吸尘板产生的电场线示意图,虚线为带负电灰尘的运动轨迹图,若带电灰尘是从A点运动到B,灰尘所受的电场力分别为FA、FB,电势分别为ϕA、ϕB,电势能分别为EA、EB,运动速度分别为vA、vB,则( )| A. | FA>FB | B. | EA<EB | C. | ϕA>ϕB | D. | vA<vB |
| A. | 3N | B. | 13N | C. | 2.5N | D. | 12N |
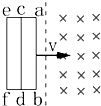 如图所示矩形金属框架的三条竖直边ab、cd、ef长均为L,电阻都为R,其余电阻不计,框架以速度v匀速地进入磁感应强度为B的匀强磁场中,设ab、cd、ef三条边先后进入磁场时,ab边两端的电压分别为U1,U2,和U3,则( )
如图所示矩形金属框架的三条竖直边ab、cd、ef长均为L,电阻都为R,其余电阻不计,框架以速度v匀速地进入磁感应强度为B的匀强磁场中,设ab、cd、ef三条边先后进入磁场时,ab边两端的电压分别为U1,U2,和U3,则( )| A. | U1=$\frac{BLv}{3}$ | B. | U2=2U1 | C. | U3=0 | D. | U1=U2=U3 |
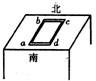 根据地磁场的特征可知,在北半球的地磁场有一水平向北的分量Bx和一个竖直向下的分量By,某研究性小组设计了如图所示实验测量Bx和By的大小,将一个电阻为R的长方形线圈abcd沿着磁针所指的南北方向平放在北半球的一个水平桌面上,测得线圈两边的长度为ab=L1,bc=L2,现突然将线圈翻转180°,使ab边与dc边互换位置,用冲击电流计测得线圈中流过的电荷量为q1,然后维持bc边不动,将线圈绕bc边转动,使线圈突然竖直,这次测得线圈中流过的电荷量为q2,则( )
根据地磁场的特征可知,在北半球的地磁场有一水平向北的分量Bx和一个竖直向下的分量By,某研究性小组设计了如图所示实验测量Bx和By的大小,将一个电阻为R的长方形线圈abcd沿着磁针所指的南北方向平放在北半球的一个水平桌面上,测得线圈两边的长度为ab=L1,bc=L2,现突然将线圈翻转180°,使ab边与dc边互换位置,用冲击电流计测得线圈中流过的电荷量为q1,然后维持bc边不动,将线圈绕bc边转动,使线圈突然竖直,这次测得线圈中流过的电荷量为q2,则( )| A. | By=$\frac{R{q}_{1}}{{L}_{1}{L}_{2}}$ | B. | By=$\frac{R{q}_{1}}{2{L}_{1}{L}_{2}}$ | ||
| C. | Bx=$\frac{R(2{q}_{2}+{q}_{1})}{2{L}_{1}{L}_{2}}$ | D. | Bx=$\frac{R(2{q}_{2}-{q}_{1})}{2{L}_{1}{L}_{2}}$ |
| A. | 它的速度等于7.9km/s | |
| B. | 它的周期是24h,且轨道平面与赤道平面重合 | |
| C. | 它的加速度等于9.8m/s2 | |
| D. | 它处于平衡伏态,且其有一定的高度 |
 如图所示,一硬杆上端绞于屋顶,用一水平力将其下端缓慢拉起.在杆从竖直拉至接近水平的过程中,拉力的变化情况是增大,拉力力矩的变化情况是增大.
如图所示,一硬杆上端绞于屋顶,用一水平力将其下端缓慢拉起.在杆从竖直拉至接近水平的过程中,拉力的变化情况是增大,拉力力矩的变化情况是增大.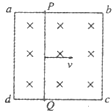 固定在匀强磁场中的正方形导体框abcd边长为L,导体框是由均匀的电阻丝围成,每条边的电阻均为R.磁场的磁感应强度为B,方向垂直于纸面向里,现将一段阻值为$\frac{1}{36}$R的电阻丝PQ架在导体框上,如图所示,若PQ以恒定的速度v从ad滑到bc,当其滑过$\frac{1}{3}$L的距离时,求:
固定在匀强磁场中的正方形导体框abcd边长为L,导体框是由均匀的电阻丝围成,每条边的电阻均为R.磁场的磁感应强度为B,方向垂直于纸面向里,现将一段阻值为$\frac{1}{36}$R的电阻丝PQ架在导体框上,如图所示,若PQ以恒定的速度v从ad滑到bc,当其滑过$\frac{1}{3}$L的距离时,求: