��Ŀ����
8��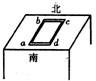 ���ݵشų���������֪���ڱ�����ĵشų���һˮƽ�ķ���Bx��һ����ֱ���µķ���By��ij�о���С���������ͼ��ʾʵ�����Bx��By�Ĵ�С����һ������ΪR�ij�������Ȧabcd���Ŵ�����ָ���ϱ�����ƽ���ڱ������һ��ˮƽ�����ϣ������Ȧ���ߵij���Ϊab=L1��bc=L2����ͻȻ����Ȧ��ת180�㣬ʹab����dc����λ�ã��ó�������Ʋ����Ȧ�������ĵ����Ϊq1��Ȼ��ά��bc�߲���������Ȧ��bc��ת����ʹ��ȦͻȻ��ֱ����β����Ȧ�������ĵ����Ϊq2��������
���ݵشų���������֪���ڱ�����ĵشų���һˮƽ�ķ���Bx��һ����ֱ���µķ���By��ij�о���С���������ͼ��ʾʵ�����Bx��By�Ĵ�С����һ������ΪR�ij�������Ȧabcd���Ŵ�����ָ���ϱ�����ƽ���ڱ������һ��ˮƽ�����ϣ������Ȧ���ߵij���Ϊab=L1��bc=L2����ͻȻ����Ȧ��ת180�㣬ʹab����dc����λ�ã��ó�������Ʋ����Ȧ�������ĵ����Ϊq1��Ȼ��ά��bc�߲���������Ȧ��bc��ת����ʹ��ȦͻȻ��ֱ����β����Ȧ�������ĵ����Ϊq2��������| A�� | By=$\frac{R{q}_{1}}{{L}_{1}{L}_{2}}$ | B�� | By=$\frac{R{q}_{1}}{2{L}_{1}{L}_{2}}$ | ||
| C�� | Bx=$\frac{R��2{q}_{2}+{q}_{1}��}{2{L}_{1}{L}_{2}}$ | D�� | Bx=$\frac{R��2{q}_{2}-{q}_{1}��}{2{L}_{1}{L}_{2}}$ |
���� ���ݵشų���������֪���ڱ�����ĵشų������������µģ�����$Q=N\frac{����}{R}$��ֻҪ�������Ÿ�ǿ�ȵ���ֱ����By��ˮƽ����Bx��
��� �⣺����Ȧ������ʱ��������Ȧ�Ĵ�ͨ���ı仯��Ϊ����1=2ByS������$Q=N\frac{����}{R}$�����ԣ�
����1=2ByL1L2=Rq1
����Ȧ��bc����ֱվ����ʱ��������Ȧ�Ĵ�ͨ���ı仯��Ϊ����2=BxL1L2-ByL1L2�����ԣ�
����2=��Bx-By��L1L2=Rq2��
������ã�
Bx=$\frac{R��2{q}_{2}+{q}_{1}��}{2{L}_{1}{L}_{2}}$
By=$\frac{R{q}_{1}}{2{L}_{1}{L}_{2}}$
��ѡ��BC
���� ���⿼���˷����ڵ�Ÿ�Ӧ���ɵĻ������ã�֪��$Q=N\frac{����}{R}$������������ã��ѶȲ���

��ϰ��ϵ�д�
�����Ŀ
15������б����������ʻ�������������˶������в����������ǣ�������
| A�� | ���� | B�� | ֧���� | C�� | ǣ���� | D�� | Ħ���� |
20�� ��ͼ��ʾ���ɰ뾶ΪR��$\frac{3}{4}$�⻬Բ�ܺ����Ϊ45��Ĺ⻬б����ɵĹ���̶�����ֱƽ���ڣ�б���Բ��֮����СԲ��ƽ�����ӣ�һС��ǡ�ܹ���ߵ㣬��ʼ�����Ź���ڲ�˳ʱ��ת������С��ͨ��б���ʱ��Ϊ���������ٶ�Ϊg����������
��ͼ��ʾ���ɰ뾶ΪR��$\frac{3}{4}$�⻬Բ�ܺ����Ϊ45��Ĺ⻬б����ɵĹ���̶�����ֱƽ���ڣ�б���Բ��֮����СԲ��ƽ�����ӣ�һС��ǡ�ܹ���ߵ㣬��ʼ�����Ź���ڲ�˳ʱ��ת������С��ͨ��б���ʱ��Ϊ���������ٶ�Ϊg����������
 ��ͼ��ʾ���ɰ뾶ΪR��$\frac{3}{4}$�⻬Բ�ܺ����Ϊ45��Ĺ⻬б����ɵĹ���̶�����ֱƽ���ڣ�б���Բ��֮����СԲ��ƽ�����ӣ�һС��ǡ�ܹ���ߵ㣬��ʼ�����Ź���ڲ�˳ʱ��ת������С��ͨ��б���ʱ��Ϊ���������ٶ�Ϊg����������
��ͼ��ʾ���ɰ뾶ΪR��$\frac{3}{4}$�⻬Բ�ܺ����Ϊ45��Ĺ⻬б����ɵĹ���̶�����ֱƽ���ڣ�б���Բ��֮����СԲ��ƽ�����ӣ�һС��ǡ�ܹ���ߵ㣬��ʼ�����Ź���ڲ�˳ʱ��ת������С��ͨ��б���ʱ��Ϊ���������ٶ�Ϊg����������| A�� | 2$\sqrt{gR}$ | B�� | 2$\sqrt{\frac{R}{g}}$ | C�� | ��2$\sqrt{2}$-2��$\sqrt{\frac{R}{g}}$ | D�� | ��$\sqrt{10}$-$\sqrt{6}$��$\sqrt{\frac{R}{g}}$ |
18�� һ�ʵ���ԭ���������x���������Լ��ٶ�a���٣���ʱ��t0�ٶȱ�Ϊv0��������-a���ٶ��˶������ٶȱ�Ϊ-$\frac{{v}_{0}}{2}$ʱ�����ٶ��ֱ�Ϊa��ֱ���ٶȱ�Ϊ$\frac{{v}_{0}}{4}$ʱ�����ٶ��ٱ�Ϊ-a0��ֱ���ٶȱ�Ϊ-$\frac{{v}_{0}}{8}$������v-tͼ����ͼ��ʾ��������˵������ȷ���ǣ�������
һ�ʵ���ԭ���������x���������Լ��ٶ�a���٣���ʱ��t0�ٶȱ�Ϊv0��������-a���ٶ��˶������ٶȱ�Ϊ-$\frac{{v}_{0}}{2}$ʱ�����ٶ��ֱ�Ϊa��ֱ���ٶȱ�Ϊ$\frac{{v}_{0}}{4}$ʱ�����ٶ��ٱ�Ϊ-a0��ֱ���ٶȱ�Ϊ-$\frac{{v}_{0}}{8}$������v-tͼ����ͼ��ʾ��������˵������ȷ���ǣ�������
 һ�ʵ���ԭ���������x���������Լ��ٶ�a���٣���ʱ��t0�ٶȱ�Ϊv0��������-a���ٶ��˶������ٶȱ�Ϊ-$\frac{{v}_{0}}{2}$ʱ�����ٶ��ֱ�Ϊa��ֱ���ٶȱ�Ϊ$\frac{{v}_{0}}{4}$ʱ�����ٶ��ٱ�Ϊ-a0��ֱ���ٶȱ�Ϊ-$\frac{{v}_{0}}{8}$������v-tͼ����ͼ��ʾ��������˵������ȷ���ǣ�������
һ�ʵ���ԭ���������x���������Լ��ٶ�a���٣���ʱ��t0�ٶȱ�Ϊv0��������-a���ٶ��˶������ٶȱ�Ϊ-$\frac{{v}_{0}}{2}$ʱ�����ٶ��ֱ�Ϊa��ֱ���ٶȱ�Ϊ$\frac{{v}_{0}}{4}$ʱ�����ٶ��ٱ�Ϊ-a0��ֱ���ٶȱ�Ϊ-$\frac{{v}_{0}}{8}$������v-tͼ����ͼ��ʾ��������˵������ȷ���ǣ�������| A�� | �ʵ���t0���ı��˶����� | |
| B�� | �ʵ㽫��x����������ֱ���˶� | |
| C�� | �ʵ��˶���������ԭ���������Ϊv0t0 | |
| D�� | �ʵ���t0���˶���ƽ���ٶ�Ϊ$\frac{{v}_{0}}{2}$ |

 ��ͼ��ʾ��ƽ�й⻬���������ǿ�ų�B�У�B=0.4T��������abʼ���Ժ㶨���ٶ�v�ص������������˶��������L=1m������R1=R3=8����R2=2����������費�ƣ�һ�������ļ���ˮƽ���ã�������Ϊd=10mm���ڲ���һ������m=10-14kg������q=10-15C�������ڵ��K�Ͽ�ʱ���ھ�ֹ״̬����K�պ�ʱ������a=7m/s2�ļ��ٶ��ȼ������䣬g=10m/s2����
��ͼ��ʾ��ƽ�й⻬���������ǿ�ų�B�У�B=0.4T��������abʼ���Ժ㶨���ٶ�v�ص������������˶��������L=1m������R1=R3=8����R2=2����������費�ƣ�һ�������ļ���ˮƽ���ã�������Ϊd=10mm���ڲ���һ������m=10-14kg������q=10-15C�������ڵ��K�Ͽ�ʱ���ھ�ֹ״̬����K�պ�ʱ������a=7m/s2�ļ��ٶ��ȼ������䣬g=10m/s2���� Ϊ��������г�ҹ����ʻ�İ�ȫ�ԣ�С��ͬѧ�����һ�֡���˸��װ�ã���ͼ��ʾ�����г������ɰ뾶r1=5.0��10-2m�Ľ�����Ȧ���뾶r2=0.40m�Ľ�����Ȧ�;�Ե�������ɣ����ֵ��ڡ���Ȧ֮��ȼ���ؽ���4����������ÿ�����������м��������һ����ֵΪR��С���ݣ���֧����װ�д������γ��˴Ÿ�Ӧǿ��B=0.10T������ֱֽ������ġ����Ρ���ǿ�ų������ڰ뾶Ϊr1����뾶Ϊr2���ŽǦ�=$\frac{��}{6}$�������Խ��ٶȦ�=2��rad/s�����ת��ת�����������������裬���Դų��ı�ԵЧӦ��
Ϊ��������г�ҹ����ʻ�İ�ȫ�ԣ�С��ͬѧ�����һ�֡���˸��װ�ã���ͼ��ʾ�����г������ɰ뾶r1=5.0��10-2m�Ľ�����Ȧ���뾶r2=0.40m�Ľ�����Ȧ�;�Ե�������ɣ����ֵ��ڡ���Ȧ֮��ȼ���ؽ���4����������ÿ�����������м��������һ����ֵΪR��С���ݣ���֧����װ�д������γ��˴Ÿ�Ӧǿ��B=0.10T������ֱֽ������ġ����Ρ���ǿ�ų������ڰ뾶Ϊr1����뾶Ϊr2���ŽǦ�=$\frac{��}{6}$�������Խ��ٶȦ�=2��rad/s�����ת��ת�����������������裬���Դų��ı�ԵЧӦ�� ��ͼ��ʾ������������ABC��Ϊ�Ÿ�Ӧǿ��ΪB����ǿ�ų�����������ABC�ǵ���ֱ�������Σ�б��AB�ij���Ϊ2L��AB��λ�ڹ⻬��Եˮƽ���ڣ��߳�bcΪ2L���߳�abΪL�ľ����ν����߿�abcd������ΪR��������F�������£��߿��Ժ㶨���ٶ�v��AB�˶���������ͼ����ʾ����ǿ�ų����涨����˳ʱ�뷽��Ϊ��������F����Ϊ�������߿����ų���ʼ��ʱ�������I������F��ʱ��ı仯ͼ��Ϊѡ���е���ͼ��������
��ͼ��ʾ������������ABC��Ϊ�Ÿ�Ӧǿ��ΪB����ǿ�ų�����������ABC�ǵ���ֱ�������Σ�б��AB�ij���Ϊ2L��AB��λ�ڹ⻬��Եˮƽ���ڣ��߳�bcΪ2L���߳�abΪL�ľ����ν����߿�abcd������ΪR��������F�������£��߿��Ժ㶨���ٶ�v��AB�˶���������ͼ����ʾ����ǿ�ų����涨����˳ʱ�뷽��Ϊ��������F����Ϊ�������߿����ų���ʼ��ʱ�������I������F��ʱ��ı仯ͼ��Ϊѡ���е���ͼ��������


