题目内容
6.观察到某一行星有颗卫星以半径R、周期T环绕此行星做圆周环绕运动,卫星的质量为m.(1)求行星的质量;
(2)求卫星的向心加速度;
(3)若行星的半径是卫星运行轨道半径的$\frac{1}{10}$,那么该行星表面的重力加速度有多大?
分析 (1)根据万有引力定律等于向心力公式,即可求出行星的质量;
(2)根据向心加速度公式求卫星的向心加速度
(3)行星表面处的重力加速度由万有引力提供即可.
解答 解:(1)卫星绕行星做匀速圆周运动,万有引力提供向心力,有
$G\frac{Mm}{{R}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}R$
解得:$M=\frac{4{π}_{\;}^{2}{R}_{\;}^{3}}{G{T}_{\;}^{2}}$
(2)卫星的向心加速度${a}_{n}^{\;}={ω}_{\;}^{2}R=(\frac{2π}{T})_{\;}^{2}R=\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}R$
(3)根据题意,行星的半径${R}_{行}^{\;}=\frac{R}{10}$
行星表面物体重力等于万有引力,有
$mg=G\frac{Mm}{(\frac{R}{10})_{\;}^{2}}$
解得:$g=100G\frac{M}{{R}_{\;}^{2}}=\frac{400{π}_{\;}^{2}R}{{T}_{\;}^{2}}$
答:(1)求行星的质量$\frac{4{π}_{\;}^{2}{R}_{\;}^{3}}{G{T}_{\;}^{2}}$;
(2)求卫星的向心加速度$\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}R$;
(3)若行星的半径是卫星运行轨道半径的$\frac{1}{10}$,那么该行星表面的重力加速度有多大$\frac{400{π}_{\;}^{2}R}{{T}_{\;}^{2}}$
点评 该题考查万有引力定律的一般应用,直接使用万有引力提供向心力的公式即可,它们非常简单

练习册系列答案
相关题目
11. 如图所示,$\frac{1}{p}$-V图中的a→b→c→d→a为一定质量的理想气体从状态a开始按箭头方向所经历的一个循环过程,以下说法中正确的是( )
如图所示,$\frac{1}{p}$-V图中的a→b→c→d→a为一定质量的理想气体从状态a开始按箭头方向所经历的一个循环过程,以下说法中正确的是( )
 如图所示,$\frac{1}{p}$-V图中的a→b→c→d→a为一定质量的理想气体从状态a开始按箭头方向所经历的一个循环过程,以下说法中正确的是( )
如图所示,$\frac{1}{p}$-V图中的a→b→c→d→a为一定质量的理想气体从状态a开始按箭头方向所经历的一个循环过程,以下说法中正确的是( )| A. | 理想气体由a→b的过程做等温变化,从c→d也做等温变化 | |
| B. | 理想气体由b→c的过程温度降低 | |
| C. | 理想气体由d→a的过程中,气体对外界做功为W=p0(Va-Vd) | |
| D. | 若理想气体装在导热性能良好的密闭容器中,则气体由b→c的过程中,单位时间内撞击到容器壁单位面积上的气体分子数减少 | |
| E. | 由a→b的过程中,气体将吸收的热量全部对外做功,违背了热力学第二定律 |
18.有一条河,宽度为d,它在静水中航行速度为v,水速为1.25v,现在小船从某一地点向河对岸开去,已知小船想用最短时间渡河,则船渡河时间为( )
| A. | $\frac{5d}{3v}$ | B. | $\frac{3d}{5v}$ | C. | $\frac{d}{v}$ | D. | $\frac{4d}{5v}$ |
15.下列说法正确的是( )
| A. | 行星在远离太阳的过程中速度越来越大 | |
| B. | 所有行星轨道的半长轴的二次方跟公转周期的三次方的比值都相同 | |
| C. | 行星轨道的长半轴越长,公转周期越大 | |
| D. | 万有引力定律对质量大的物体适用,对质量小的物体不适用 |
1. 两根相互平行的光滑金属导轨水平放置于如图所示的匀强磁场中,在导轨上接触良好的导体棒AB和CD可以自由滑动.当AB以速度v向右运动时,下列说法中正确的是( )
两根相互平行的光滑金属导轨水平放置于如图所示的匀强磁场中,在导轨上接触良好的导体棒AB和CD可以自由滑动.当AB以速度v向右运动时,下列说法中正确的是( )
 两根相互平行的光滑金属导轨水平放置于如图所示的匀强磁场中,在导轨上接触良好的导体棒AB和CD可以自由滑动.当AB以速度v向右运动时,下列说法中正确的是( )
两根相互平行的光滑金属导轨水平放置于如图所示的匀强磁场中,在导轨上接触良好的导体棒AB和CD可以自由滑动.当AB以速度v向右运动时,下列说法中正确的是( )| A. | 开始一段时间,导体棒CD内有电流通过,方向是D→C | |
| B. | 开始一段时间,导体棒CD内有电流通过,方向是C→D | |
| C. | 开始一段时间,磁场对导体棒CD的作用力向左 | |
| D. | 最终两导体棒速度相等,电流为零 |
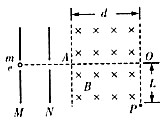 电子自静止开始经M、N板间(两板间的电压为U)的电场加速后从A点垂直于磁场边界射入宽度为d的有平行边界的匀强磁场中,电子离开磁场时的位置P偏离入射方向的距离为L,如图所示.求匀强磁场的磁感应强度.
电子自静止开始经M、N板间(两板间的电压为U)的电场加速后从A点垂直于磁场边界射入宽度为d的有平行边界的匀强磁场中,电子离开磁场时的位置P偏离入射方向的距离为L,如图所示.求匀强磁场的磁感应强度. 如图,底面较大的气缸内盛有密度为ρ的某种液体,液面距离气缸口为l,粗细均匀的小玻璃瓶底朝上漂浮在液体中,平衡时小瓶露出液面的部分为h,液面下瓶内还有4h长的空气柱.现用活塞将气缸封闭(图中未画出),使活塞缓慢向下运动,各部分气体的温度均保持不变,直到瓶底与液面相平(瓶口未触及缸底).已知大气压为p0,重力加速度为g,求活塞下推的距离.
如图,底面较大的气缸内盛有密度为ρ的某种液体,液面距离气缸口为l,粗细均匀的小玻璃瓶底朝上漂浮在液体中,平衡时小瓶露出液面的部分为h,液面下瓶内还有4h长的空气柱.现用活塞将气缸封闭(图中未画出),使活塞缓慢向下运动,各部分气体的温度均保持不变,直到瓶底与液面相平(瓶口未触及缸底).已知大气压为p0,重力加速度为g,求活塞下推的距离. 如图所示,质量为2m的小滑块P和质量为m的小滑块Q都视作质点,与轻质弹簧相连的Q静止在光滑水平面上.P以某一初速度v向Q运动并与弹簧发生碰撞,碰撞过程中,当弹簧的弹性势能最大时,Q的速度大小为$\frac{2}{3}$v;此时弹簧的最大弹性势能为$\frac{1}{3}$mv2.
如图所示,质量为2m的小滑块P和质量为m的小滑块Q都视作质点,与轻质弹簧相连的Q静止在光滑水平面上.P以某一初速度v向Q运动并与弹簧发生碰撞,碰撞过程中,当弹簧的弹性势能最大时,Q的速度大小为$\frac{2}{3}$v;此时弹簧的最大弹性势能为$\frac{1}{3}$mv2.