题目内容
14.某人造卫星距地面高h,地球半径为R,地面重力加速度g0,分别用h、R、g0表示卫星周期T、线速度v、角速度ω.分析 根据万有引力提供圆周运动向心力,求得卫星周期、线速度和角速度与轨道半径的表示式;
在地球表面重力与万有引力相等,由重力加速度和地球半径求出地球质量,再求解即可.
解答 解:设卫星的轨道半径为r,地球的质量为M.则 r=R+h
根据万有引力提供圆周运动向心力,有:
G$\frac{Mm}{{r}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}$r=m$\frac{{v}^{2}}{r}$=mω2r
解得,卫星运动的周期 T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,线速度 v=$\sqrt{\frac{GM}{r}}$,角速度ω=$\sqrt{\frac{GM}{{r}^{3}}}$
在地球表面,由mg0=G$\frac{Mm}{{R}^{2}}$,得GM=g0R2;
联立解得 $T=\frac{2π}{R}\sqrt{\frac{{{{(R+h)}^3}}}{g_0}}$,$v=\sqrt{\frac{{{g_0}{R^2}}}{R+h}}$,ω=$\sqrt{\frac{{g}_{0}{R}^{2}}{(R+h)^{3}}}$
答:卫星周期T、线速度v、角速度ω分别为:$T=\frac{2π}{R}\sqrt{\frac{{{{(R+h)}^3}}}{g_0}}$,$v=\sqrt{\frac{{{g_0}{R^2}}}{R+h}}$,ω=$\sqrt{\frac{{g}_{0}{R}^{2}}{(R+h)^{3}}}$.
点评 万有引力应用的两个关键:一是在星球表面重力与万有引力相等,二是万有引力提供环绕天体圆周运动的向心力,掌握并灵活运用万有引力与向心力公式是正确解题的关键.

练习册系列答案
相关题目
2.下列说法正确的是( )
| A. | 只要能减弱气体分子热运动的剧烈程度,气体的温度就可以降低 | |
| B. | 雪花是晶体,可以有不同的形状 | |
| C. | 当分子间的引力和斥力平衡时,分子势能最大 | |
| D. | 液晶电视的显示器利用了液晶对光具有各向同性作用的特点 | |
| E. | 液体的饱和汽压随温度升高而增大 |
9.如图所示的皮带传动装置中,轮A和轮B同轴,A、B、C分别是三个轮边缘上的质点,则( )

| A. | 质点A和质点B的线速度大小相等 | B. | 质点A和质点B的角速度大小相等 | ||
| C. | 质点B和质点C的线速度大小相等 | D. | 质点B和质点C的角速度大小相等 |
19.下列说法中正确的是( )
| A. | 氢原子从激发态向基态跃迁可以辐射任何频率的光子 | |
| B. | 铀235的半衰期约为7亿年,随地球环境的变化,半衰期不变 | |
| C. | β射线与γ射线一样都是电磁波,但穿透本领远比γ射线弱 | |
| D. | 任何金属都存在一个“极限波长”,入射光的波长必须小于这个波长,才能产生光电效应 |
3. 如图所示,两物体用两根轻质细线分别悬挂在天花板上,两细线与水平方向夹角分别为60°和45°,A、B间拴接的轻质弹簧恰好处于水平状态,则下列判断正确的是( )
如图所示,两物体用两根轻质细线分别悬挂在天花板上,两细线与水平方向夹角分别为60°和45°,A、B间拴接的轻质弹簧恰好处于水平状态,则下列判断正确的是( )
 如图所示,两物体用两根轻质细线分别悬挂在天花板上,两细线与水平方向夹角分别为60°和45°,A、B间拴接的轻质弹簧恰好处于水平状态,则下列判断正确的是( )
如图所示,两物体用两根轻质细线分别悬挂在天花板上,两细线与水平方向夹角分别为60°和45°,A、B间拴接的轻质弹簧恰好处于水平状态,则下列判断正确的是( )| A. | A、B的质量之比为1:$\sqrt{3}$ | |
| B. | A、B所受弹簧弹力大小之比为$\sqrt{3}$:$\sqrt{2}$ | |
| C. | 悬挂A、B的细线上拉力大小之比为$\sqrt{2}$:1 | |
| D. | 悬挂A、B的细线上拉力大小之比为1:$\sqrt{3}$ |
4.起重机以1m/s2的加速度将质量为1 000kg的货物由静止开始匀加速向上提升,g取10m/s2,则起重机对货物做的功率是( )
| A. | 500W | B. | 4 500 W | C. | 5 000W | D. | 5 500 W |
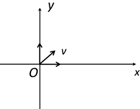 如图,图中坐标原点O(0,0)处有一带电粒子源,沿xOy平面内向y≥0,x≥0的区域内的各个方向发射粒子.粒子的速率均为v,质量均为m,电量均为+q.有人设计了方向垂直于xOy平面向里、磁感应强度为B的匀强磁场区域,使上述所有带电粒子从该区域的边界射出时均能沿y轴负方向运动,不考虑粒子间相互作用,不计粒子重力.试求:
如图,图中坐标原点O(0,0)处有一带电粒子源,沿xOy平面内向y≥0,x≥0的区域内的各个方向发射粒子.粒子的速率均为v,质量均为m,电量均为+q.有人设计了方向垂直于xOy平面向里、磁感应强度为B的匀强磁场区域,使上述所有带电粒子从该区域的边界射出时均能沿y轴负方向运动,不考虑粒子间相互作用,不计粒子重力.试求:


