题目内容
16.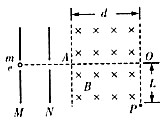 电子自静止开始经M、N板间(两板间的电压为U)的电场加速后从A点垂直于磁场边界射入宽度为d的有平行边界的匀强磁场中,电子离开磁场时的位置P偏离入射方向的距离为L,如图所示.求匀强磁场的磁感应强度.
电子自静止开始经M、N板间(两板间的电压为U)的电场加速后从A点垂直于磁场边界射入宽度为d的有平行边界的匀强磁场中,电子离开磁场时的位置P偏离入射方向的距离为L,如图所示.求匀强磁场的磁感应强度.(已知电子的质量为m,电荷量为e)
分析 根据动能定理求出电子经电场加速后的速度,根据几何关系求出粒子在磁场中的半径,结合半径公式求出磁感应强度的大小.
解答 解:电子经电场加速后,根据动能定理有:$eU=\frac{1}{2}m{v^2}$…①
电子进入磁场后,洛伦兹力充当向心力:$eBv=m\frac{v^2}{r}$…②
由几何关系得:r2=d2+(r-L)2…③
由①②③解得:B=$\frac{{2L\sqrt{\frac{2mU}{e}}}}{{{d^2}+{L^2}}}$=$\frac{2L\sqrt{2meU}}{e({d}^{2}+{L}^{2})}$.
答:匀强磁场的磁感应强度为$\frac{2L\sqrt{2meU}}{e({d}^{2}+{L}^{2})}$.
点评 本题是带电粒子在磁场中运动的问题,关键是画出轨迹,由几何知识求解轨迹半径.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
18.下列错误的是( )
| A. | 牛顿发现摆的等时性 | |
| B. | 伽利略首先将物理实验事实和逻辑 | |
| C. | 卡文迪许测量了万有引力常量 | |
| D. | 洛伦兹发现了磁场对运用电荷的作用公式 |
7. 如图所示,在放上小物体A之前,长木板B恰好沿C的足够长斜面匀速下滑,B与斜面间的动摩擦因数为μ,B的上表面光滑,在B匀速下滑过程中轻轻放上小物体A(C物体始终保持静止),下列说法正确的是:( )
如图所示,在放上小物体A之前,长木板B恰好沿C的足够长斜面匀速下滑,B与斜面间的动摩擦因数为μ,B的上表面光滑,在B匀速下滑过程中轻轻放上小物体A(C物体始终保持静止),下列说法正确的是:( )
 如图所示,在放上小物体A之前,长木板B恰好沿C的足够长斜面匀速下滑,B与斜面间的动摩擦因数为μ,B的上表面光滑,在B匀速下滑过程中轻轻放上小物体A(C物体始终保持静止),下列说法正确的是:( )
如图所示,在放上小物体A之前,长木板B恰好沿C的足够长斜面匀速下滑,B与斜面间的动摩擦因数为μ,B的上表面光滑,在B匀速下滑过程中轻轻放上小物体A(C物体始终保持静止),下列说法正确的是:( )| A. | B仍然匀速下滑 | |
| B. | B减速下滑 | |
| C. | A加速下滑 | |
| D. | 地面对C的摩擦力可能向左、也可能向右 |
1.下列说法正确的是( )
| A. | 方程式${\;}_{92}^{238}$U→${\;}_{90}^{234}$Th+${\;}_{2}^{4}$He是重核裂变反应方程 | |
| B. | 光电效应和康普顿效应都说明光具有粒子性 | |
| C. | 衰变所释放的电子是原子核内的中子转化成质子时所产生的 | |
| D. | 比结合能越大,原子核中核子结合的越牢固,原子核越稳定 | |
| E. | 在光电效应实验中,某金属的截止频率对应的波长为λ0,若用波长为λ(λ>λ0)的单色光做该实验,会产生光电效应 |
8.下列说法中正确的是( )


| A. | 卢瑟福通过实验发现质子的核反应方程为${\;}_{2}^{4}$He+${\;}_{7}^{14}$N→${\;}_{8}^{17}$O+${\;}_{1}^{1}$H | |
| B. | 放射性元素的半衰期随温度的升高而增加 | |
| C. | 一个动量为p的电子对应的物质波波长为hp(h为普朗克常量) | |
| D. | 从能级图中可知,氢原子从n=2能级跃迁到n=1能级释放出的光子能量高于从n=4能级跃迁到n=2能级所释放出的光子能量 |
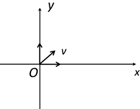 如图,图中坐标原点O(0,0)处有一带电粒子源,沿xOy平面内向y≥0,x≥0的区域内的各个方向发射粒子.粒子的速率均为v,质量均为m,电量均为+q.有人设计了方向垂直于xOy平面向里、磁感应强度为B的匀强磁场区域,使上述所有带电粒子从该区域的边界射出时均能沿y轴负方向运动,不考虑粒子间相互作用,不计粒子重力.试求:
如图,图中坐标原点O(0,0)处有一带电粒子源,沿xOy平面内向y≥0,x≥0的区域内的各个方向发射粒子.粒子的速率均为v,质量均为m,电量均为+q.有人设计了方向垂直于xOy平面向里、磁感应强度为B的匀强磁场区域,使上述所有带电粒子从该区域的边界射出时均能沿y轴负方向运动,不考虑粒子间相互作用,不计粒子重力.试求:



