题目内容
11. 如图所示,在光滑水平面上放着A、B、C三个物块,A、B、C的质量依次是m、2m、3m.现让A物块以初速度v0向B运动,A、B相碰后不再分开,共同向C运动;它们和C相碰后也不再分开,ABC共同向右运动.求:
如图所示,在光滑水平面上放着A、B、C三个物块,A、B、C的质量依次是m、2m、3m.现让A物块以初速度v0向B运动,A、B相碰后不再分开,共同向C运动;它们和C相碰后也不再分开,ABC共同向右运动.求:(1)ABC共同向右运动的速度v的大小.
(2)A、B碰撞过程中的动能损失△EK.
(3)AB与C碰撞过程B物块对C物块的冲量I.
分析 (1)以A、B、C整体为对象,全过程应用动量守恒定律列式,可求得ABC共同向右运动的速度v.
(2)根据动量守恒定律求出A、B碰后瞬间的共同速度.再由能量守恒定律求A、B碰撞过程中的动能损失△EK.
(3)以C为研究对象,AB与C碰撞过程应用动量定理求AB与C碰撞过程B物块对C物块的冲量I.
解答 解:(1)以A、B、C整体为对象,取向右为正方向,全过程应用动量守恒定律:mv0=(m+2m+3m)v
得ABC共同向右运动的速度 $v=\frac{v_0}{6}$
(2)设A、B碰撞后的速度为v',根据动量守恒有 mv0=(m+2m)v'
动能损失 $△{E_K}=\frac{1}{2}mv_0^2-\frac{1}{2}({m+2m}){v'^2}$
解得 $△{E_K}=\frac{1}{3}mv_0^2$.
(3)以C为研究对象,AB与C碰撞过程应用动量定理,B物块对C物块的冲量等于C物块的动量变化 $I=3mv=\frac{1}{2}m{v_0}$
方向水平向右.
答:
(1)ABC共同向右运动的速度v的大小是$\frac{{v}_{0}}{6}$.
(2)A、B碰撞过程中的动能损失△EK是$\frac{1}{3}m{v}_{0}^{2}$
(3)AB与C碰撞过程B物块对C物块的冲量I是$\frac{1}{2}m{v}_{0}$,方向水平向右.
点评 分析物理过程,把握每个过程所遵循的物理规律是应培养的能力.此题中涉及碰撞,关键要掌握碰撞的基本规律动量守恒定律和能量守恒定律,并要知道动量定理是求冲量的方法之一.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.从同一位置以相同的速率把完全相同的甲、乙、丙三个小球分别竖直向上、竖直向下及水平抛出后落到同一水平地面上.不计空气阻力,不考虑小球反弹,则( )
| A. | 落地时乙球的动能最大 | B. | 落地时甲球的动能最大 | ||
| C. | 丙球的重力做功的平均功率最小 | D. | 落地时丙球重力的瞬时功率最小 |
19. 如图甲所示,在光滑水平面上的两个小球发生正碰,小球的质量分别为m1和m2,图乙为它们碰撞前后的x-t图象.已知m1=0.1kg,由此可以判断( )
如图甲所示,在光滑水平面上的两个小球发生正碰,小球的质量分别为m1和m2,图乙为它们碰撞前后的x-t图象.已知m1=0.1kg,由此可以判断( )
 如图甲所示,在光滑水平面上的两个小球发生正碰,小球的质量分别为m1和m2,图乙为它们碰撞前后的x-t图象.已知m1=0.1kg,由此可以判断( )
如图甲所示,在光滑水平面上的两个小球发生正碰,小球的质量分别为m1和m2,图乙为它们碰撞前后的x-t图象.已知m1=0.1kg,由此可以判断( )| A. | 碰后m2和m1都向右运动 | |
| B. | 碰前m1静止,m2向右运动 | |
| C. | 碰撞过程中系统损失了0.4J的机械能 | |
| D. | 由动量守恒可以算出m2=0.3kg |
13. 如图所示,带有等量异种电荷相距10cm的平行板A和B之间有一个匀强电场,其中A板接地,电场强度E=2×102V/m,方向向下,电场中C点距B板3cm,D点距A板4cm,现将A板向下移动2cm,则( )
如图所示,带有等量异种电荷相距10cm的平行板A和B之间有一个匀强电场,其中A板接地,电场强度E=2×102V/m,方向向下,电场中C点距B板3cm,D点距A板4cm,现将A板向下移动2cm,则( )
 如图所示,带有等量异种电荷相距10cm的平行板A和B之间有一个匀强电场,其中A板接地,电场强度E=2×102V/m,方向向下,电场中C点距B板3cm,D点距A板4cm,现将A板向下移动2cm,则( )
如图所示,带有等量异种电荷相距10cm的平行板A和B之间有一个匀强电场,其中A板接地,电场强度E=2×102V/m,方向向下,电场中C点距B板3cm,D点距A板4cm,现将A板向下移动2cm,则( )| A. | C、D两点间的电势差的变化量△UCD=1.5V | |
| B. | C、D两点的电势都降低 | |
| C. | 将一个电子放在D点,在A板下移的过程中电场力对电子做的功为4eV | |
| D. | A板下移后,一个电子从C点移动到D点,电场力对电子做的功为-6eV |
 如图所示,两根足够长的光滑平行金属导轨MN、PQ间距离L=0.5m,其电阻不计,两导轨及其构成的平面与水平面成30°角.完全相同的两金属棒ab、cd分别垂直导轨放置,且都与导轨始终有良好接触.已知两金属棒质量均为m=0.5kg,电阻相等且不可忽略.整个装置处在垂直于导轨平面向上的匀强磁场中,磁感应强度B=4T,金属棒ab在平行于导轨向上的力F作用下,沿导轨向上匀速运动,而金属棒cd恰好能够保持静止.取g=10m/s2,求:
如图所示,两根足够长的光滑平行金属导轨MN、PQ间距离L=0.5m,其电阻不计,两导轨及其构成的平面与水平面成30°角.完全相同的两金属棒ab、cd分别垂直导轨放置,且都与导轨始终有良好接触.已知两金属棒质量均为m=0.5kg,电阻相等且不可忽略.整个装置处在垂直于导轨平面向上的匀强磁场中,磁感应强度B=4T,金属棒ab在平行于导轨向上的力F作用下,沿导轨向上匀速运动,而金属棒cd恰好能够保持静止.取g=10m/s2,求: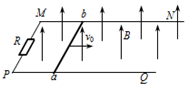 如图所示,水平面上有两根足够长的光滑平行金属导轨MN和PQ,两导轨间距为L,电阻均可忽略不计,在M和P之间接有阻值为R的定值电阻.导体杆ab质量为m,电阻为r,并与导轨接触良好.整个装置处于方向竖直向上、磁感应强度为B的匀强磁场中.现给ab杆大小为v0的初速度,使杆向右运动.求:
如图所示,水平面上有两根足够长的光滑平行金属导轨MN和PQ,两导轨间距为L,电阻均可忽略不计,在M和P之间接有阻值为R的定值电阻.导体杆ab质量为m,电阻为r,并与导轨接触良好.整个装置处于方向竖直向上、磁感应强度为B的匀强磁场中.现给ab杆大小为v0的初速度,使杆向右运动.求: