题目内容
14.据报道,美国国家航空航天局宣布首次在太阳系外发现“类地”行星,假如宇航员乘坐宇宙飞船到达该行星,进行科学观测,得到该行星的自转周期为T;宇航员在该行星“北极”距该行星地面附近h处自由释放一个小球(引力视为恒力),落地时间为t.已知该行星半径为R,万有引力常量为G,则下列说法正确的是( )| A. | 该行星的第一宇宙速度为$\frac{πR}{T}$ | |
| B. | 宇宙飞船绕该星球做圆周运动的周期不小于πt$\sqrt{\frac{2R}{h}}$ | |
| C. | 该行星的平均密度为$\frac{3π}{{T}^{2}G}$ | |
| D. | 如果该行星存在一颗同步卫星,其距行星表面高度为$\root{3}{\frac{h{T}^{2}{R}^{2}}{2{π}^{2}{t}^{2}}}$-R |
分析 根据自由落体运动求出星球表面的重力加速度,再根据万有引力提供圆周运动向心力讨论即可.
解答 解:根据自由落体运动求得星球表面的重力加速度$g=\frac{2h}{{t}^{2}}$,
A、星球的第一宇宙速度$v=\sqrt{gR}=\sqrt{\frac{2hR}{{t}^{2}}}$,故A错误;
B、根据万有引力提供圆周运动向心力有:G$\frac{Mm}{{r}^{2}}$=m$(\frac{2π}{T})^{2}r$,垃圾的运行周期:T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,可知轨道半径越小周期越小,卫星的最小半径为R,则周期最小${T}_{min}=2π\sqrt{\frac{{R}^{3}}{GM}}$=πt$\sqrt{\frac{2R}{h}}$,故B正确;
C、由$G\frac{Mm}{{R}^{2}}=mg\frac{2h}{{t}^{2}}$有:M=$\frac{2h{R}^{2}}{G{t}^{2}}$,所以星球的密度$ρ=\frac{M}{V}=\frac{3h}{2G{t}^{2}Rπ}$,故C错误;
D、同步卫星的周期与星球自转周期相同故有:$G\frac{Mm}{(R+h)^{2}}=m\frac{4{π}^{2}(R+h)}{{T}^{2}}$,代入数据解得:h=$\root{3}{\frac{h{T}^{2}{R}^{2}}{2{π}^{2}{t}^{2}}}$-R,故D正确.
故选:BD
点评 本题关键是通过自由落体运动求出星球表面的重力加速度,再根据万有引力提供圆周运动向心力和万有引力等于重力求解.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
4.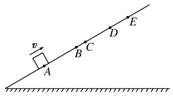 如图所示,一小滑块(可视为质点)沿足够长的光滑斜面以初速度v向上做匀变速直线运动,依次经A、B、C、D到达最高点E,然后又以相同的加速度从E点回到A点,已知AB=BD,BC=1m,滑块在上滑过程中从A到C和从C到D所用的时间相等,滑块两次经过A点的时间为16s,两次经过D点的时间为8s.则( )
如图所示,一小滑块(可视为质点)沿足够长的光滑斜面以初速度v向上做匀变速直线运动,依次经A、B、C、D到达最高点E,然后又以相同的加速度从E点回到A点,已知AB=BD,BC=1m,滑块在上滑过程中从A到C和从C到D所用的时间相等,滑块两次经过A点的时间为16s,两次经过D点的时间为8s.则( )
 如图所示,一小滑块(可视为质点)沿足够长的光滑斜面以初速度v向上做匀变速直线运动,依次经A、B、C、D到达最高点E,然后又以相同的加速度从E点回到A点,已知AB=BD,BC=1m,滑块在上滑过程中从A到C和从C到D所用的时间相等,滑块两次经过A点的时间为16s,两次经过D点的时间为8s.则( )
如图所示,一小滑块(可视为质点)沿足够长的光滑斜面以初速度v向上做匀变速直线运动,依次经A、B、C、D到达最高点E,然后又以相同的加速度从E点回到A点,已知AB=BD,BC=1m,滑块在上滑过程中从A到C和从C到D所用的时间相等,滑块两次经过A点的时间为16s,两次经过D点的时间为8s.则( )| A. | 通过A点的速率为8 m/s | B. | 通过B点的速率为$\sqrt{10}$ m/s | ||
| C. | 通过C点的速率为6 m/s | D. | CD:DE=5:4 |
19.下列关于内能的说法中,正确的是( )
| A. | 不同的物体,若温度相等,则内能也相等 | |
| B. | 物体速度增大,则分子动能增大,内能也增大 | |
| C. | 冰熔解成水,温度不变,则内能也不变 | |
| D. | 对物体做功或向物体传热,都可能改变物体的内能 |
4.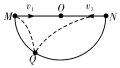 同时将两个小球以v1、v2的速度沿如图所示的方向抛出,发现两球刚好落在一个截面为半圆形的坑中同一点Q,已知∠MOQ=60°.忽略空气的阻力.则下列说法正确的是( )
同时将两个小球以v1、v2的速度沿如图所示的方向抛出,发现两球刚好落在一个截面为半圆形的坑中同一点Q,已知∠MOQ=60°.忽略空气的阻力.则下列说法正确的是( )
 同时将两个小球以v1、v2的速度沿如图所示的方向抛出,发现两球刚好落在一个截面为半圆形的坑中同一点Q,已知∠MOQ=60°.忽略空气的阻力.则下列说法正确的是( )
同时将两个小球以v1、v2的速度沿如图所示的方向抛出,发现两球刚好落在一个截面为半圆形的坑中同一点Q,已知∠MOQ=60°.忽略空气的阻力.则下列说法正确的是( )| A. | $\frac{{v}_{1}}{{v}_{2}}$=$\frac{1}{3}$ | |
| B. | 仅增大v1,v2,则两球在坑中落点均在Q点右侧 | |
| C. | 两球的初速度无论怎样变化,只要落在坑中的同一点,v1+v2就为常数 | |
| D. | 若仅增大v1,则两球可在落在坑中前相遇 |
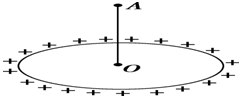 如图所示,一个均匀的带电圆环,带电荷量为+Q,半径为r,放在绝缘水平桌面上.圆心为O点,过O点作一竖直线,在此线上取一点A,使A到O点的距离为0.75r,在A点放一检验电荷-q,则-q在A点所受的库仑力大小为$\frac{48kQq}{125{r}^{2}}$.
如图所示,一个均匀的带电圆环,带电荷量为+Q,半径为r,放在绝缘水平桌面上.圆心为O点,过O点作一竖直线,在此线上取一点A,使A到O点的距离为0.75r,在A点放一检验电荷-q,则-q在A点所受的库仑力大小为$\frac{48kQq}{125{r}^{2}}$.
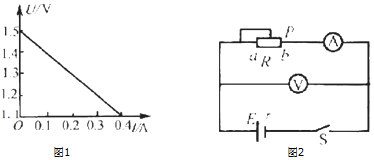
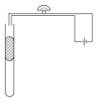 如图所示为火灾报警器的原理图,竖直放置的玻璃试管中装入水银,当温度升高时,水银柱上升,使电路导通,蜂鸣器发出响声,在25℃时,下端封闭的空气柱长为L1=20cm,水银柱上表面与导线端点的距离为L2=10cm,管内水银柱的重量为8N,横截面积为1cm2,大气压强p0=1.0×105 Pa,问:
如图所示为火灾报警器的原理图,竖直放置的玻璃试管中装入水银,当温度升高时,水银柱上升,使电路导通,蜂鸣器发出响声,在25℃时,下端封闭的空气柱长为L1=20cm,水银柱上表面与导线端点的距离为L2=10cm,管内水银柱的重量为8N,横截面积为1cm2,大气压强p0=1.0×105 Pa,问: