题目内容
8.随着我国登月计划的实施,我国宇航员登上月球已不是梦想.假如我国宇航员登上月球并在月球表面附近以初速度v0竖直向上抛出一个小球,经时间t后回到出发点.已知月球的半径为R,万有引力常量为G,则下列说法正确的是( )| A. | 月球表面的重力加速度为$\frac{{v}_{0}}{t}$ | |
| B. | 月球的质量为$\frac{{v}_{0}{R}^{2}}{Gt}$ | |
| C. | 宇航员在月球表面附近绕月球做匀速圆周运动的绕行周期为2π$\sqrt{\frac{Rt}{{v}_{0}}}$ | |
| D. | 宇航员在月球表面获得$\sqrt{\frac{2{v}_{0}R}{t}}$的速度就可能离开月球表面围绕月球做圆周运动 |
分析 AB、小球在月球表面做竖直上抛运动,由t=$\frac{2{v}_{0}}{{g}_{月}}$求出月球表面的重力加速度,物体在月球表面上时,由重力等于地月球的万有引力求出月球的质量.
C、宇航员乘坐飞船在月球表面附近绕月球做匀速圆周运动,根据重力提供向心力求得绕行周期.
D、宇航员离开月球表面围绕月球做圆周运动至少应获得的速度大小即月球的第一宇宙速度大小.
解答 解:A、小球在月球表面做竖直上抛运动,根据匀变速运动规律得:t=$\frac{2{v}_{0}}{{g}_{月}}$;
解得:g月=$\frac{2{v}_{0}}{t}$,故A错误;
B、物体在月球表面上时,由重力等于地月球的万有引力得:$G\frac{Mm}{{R}^{2}}$=mg月,解得:M=$\frac{{R}^{2}{g}_{月}}{G}$=$\frac{2{v}_{0}{R}^{2}}{Gt}$,故B错误;
C、宇航员乘坐飞船在月球表面附近绕月球做匀速圆周运动,根据重力提供向心力得:
mg月=m$\frac{4{π}^{2}R}{{T}^{2}}$=m$\frac{2{v}_{0}}{t}$
解得:T=$π\sqrt{\frac{2Rt}{{v}_{0}}}$,故C错误.
D、宇航员离开月球表面围绕月球做圆周运动至少应获得的速度大小即月球的第一宇宙速度大小
所以$G\frac{Mm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$
解得:v=$\sqrt{\frac{GM}{R}}$=$\sqrt{\frac{2{v}_{0}R}{t}}$,故D正确;
故选:D.
点评 本题是卫星类型的问题,常常建立这样的模型:环绕天体绕中心天体做匀速圆周运动,由中心天体的万有引力提供向心力.重力加速度g是联系物体运动和天体运动的桥梁.

| A. | 1 m/s | B. | 0.5 m/s | C. | 2 m/s | D. | 2.5 m/s |

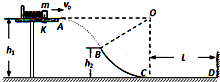 如图,在距水平地面高h1=1.2m的光滑水平台面上,一个质量m=1kg的小物块压缩弹簧后被锁定.现接触锁定,小物块与弹簧分离后将以一定的水平速度v0向右从A点滑离平台,并恰好从B点沿切线方向进入光滑竖直的圆弧轨道BC.已知B点距水平地面的高h2=0.6m,圆弧轨道BC的圆心O与水平台面等高,C点的切线水平,并与长L=2.8m的水平粗糙直轨道CD平滑连接,小物块恰能到达D处.重力加速度g=10m/s2,空气阻力忽略不计.求:
如图,在距水平地面高h1=1.2m的光滑水平台面上,一个质量m=1kg的小物块压缩弹簧后被锁定.现接触锁定,小物块与弹簧分离后将以一定的水平速度v0向右从A点滑离平台,并恰好从B点沿切线方向进入光滑竖直的圆弧轨道BC.已知B点距水平地面的高h2=0.6m,圆弧轨道BC的圆心O与水平台面等高,C点的切线水平,并与长L=2.8m的水平粗糙直轨道CD平滑连接,小物块恰能到达D处.重力加速度g=10m/s2,空气阻力忽略不计.求: 滑块A、B与C点位于一条直线上,设A、B质量均为m且可视为质点,A、B间的距离为L,B与C点间距离为S,给A-瞬时初速度v0,使A向B运动并发生对心正碰,碰撞时间极短,碰撞过程中没有能量损失,设A、B与平面的动摩擦因数为μ.求:为使B通过C点,A的初速度v0最小是多大?
滑块A、B与C点位于一条直线上,设A、B质量均为m且可视为质点,A、B间的距离为L,B与C点间距离为S,给A-瞬时初速度v0,使A向B运动并发生对心正碰,碰撞时间极短,碰撞过程中没有能量损失,设A、B与平面的动摩擦因数为μ.求:为使B通过C点,A的初速度v0最小是多大? 跳台滑雪是勇敢者的运动,运动员在专用滑雪板上,不带雪杖在助滑路上获得高速后水平飞出,在空中飞行一段距离后着陆,这项运动极为壮观.设一位运动员由a点沿水平方向跃起,到山坡b点着陆,如图所示.测得a、b间距离L=40m,山坡倾角θ=30°,山坡可以看成一个斜面.试计算:
跳台滑雪是勇敢者的运动,运动员在专用滑雪板上,不带雪杖在助滑路上获得高速后水平飞出,在空中飞行一段距离后着陆,这项运动极为壮观.设一位运动员由a点沿水平方向跃起,到山坡b点着陆,如图所示.测得a、b间距离L=40m,山坡倾角θ=30°,山坡可以看成一个斜面.试计算: