题目内容
16.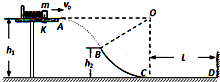 如图,在距水平地面高h1=1.2m的光滑水平台面上,一个质量m=1kg的小物块压缩弹簧后被锁定.现接触锁定,小物块与弹簧分离后将以一定的水平速度v0向右从A点滑离平台,并恰好从B点沿切线方向进入光滑竖直的圆弧轨道BC.已知B点距水平地面的高h2=0.6m,圆弧轨道BC的圆心O与水平台面等高,C点的切线水平,并与长L=2.8m的水平粗糙直轨道CD平滑连接,小物块恰能到达D处.重力加速度g=10m/s2,空气阻力忽略不计.求:
如图,在距水平地面高h1=1.2m的光滑水平台面上,一个质量m=1kg的小物块压缩弹簧后被锁定.现接触锁定,小物块与弹簧分离后将以一定的水平速度v0向右从A点滑离平台,并恰好从B点沿切线方向进入光滑竖直的圆弧轨道BC.已知B点距水平地面的高h2=0.6m,圆弧轨道BC的圆心O与水平台面等高,C点的切线水平,并与长L=2.8m的水平粗糙直轨道CD平滑连接,小物块恰能到达D处.重力加速度g=10m/s2,空气阻力忽略不计.求:(1)小物块由A到B的运动时间t;
(2)解除锁定前弹簧所储存的弹性势能Ep;
(3)小物块与轨道CD间的动摩擦因数μ.
分析 (1)首先要清楚物块的运动过程,A到B的过程为平抛运动,已知高度运用平抛运动的规律求出时间;
(2)知道运动过程中能量的转化,弹簧的弹性势能转化给物块的动能;
(3)从A点到最后停在轨道CD上的某点p,物块的动能和重力势能转化给摩擦力做功产生的内能.
解答 解:(1)小物块由A运动到B的过程中做平抛运动,在竖直方向上根据自由落体运动规律可知:
h1-h2=$\frac{1}{2}$gt2
小物块由A运动到B的时间为:t=$\sqrt{\frac{2({h}_{1}-{h}_{2})}{g}}$=$\frac{\sqrt{3}}{5}$s≈0.346s
(2)根据图中几何关系可知:h2=h1(1-cos∠BOC),
代入数据解得:∠BOC=60°
设小滑块从A点离开时速度大小为v,根据平抛运动规律有:
tan60°=$\frac{gt}{v}$,
代入数据解得:v=2m/s
根据功能关系可知,原来压缩的弹簧储存的弹性势能为t2:
Ep=$\frac{1}{2}$mv2=2J
(3)依据题意根据功能关系有:
mgh1+EP=μmgL
代入数据解得:μ=$\frac{1}{2}$.
答:(1)小物块由A到B的运动时间为0.346s;
(2)解除锁定前弹簧所储存的弹性势能为2J;
(3)小物块与轨道CD间的动摩擦因数为$\frac{1}{2}$.
点评 本题主要考查了功能关系和平抛运动基本公式的直接应用,要求同学们能正确分析物体的运动情况和受力情况,知道从A到B点过程中物体做平抛运动,做物理问题应该先清楚研究对象的运动过程,根据运动性质利用物理规律解决问题.关于能量守恒的应用,要清楚物体运动过程中能量的转化.

练习册系列答案
相关题目
6.关于地球同步卫星下列说法正确的是( )
| A. | 地球同步卫星和地球同步,因此同步卫星的高度和线速度大小是一定的 | |
| B. | 地球同步卫星的地球的角速度虽被确定,但高度和速度可以选择,高度增加,速度增大,高度降低,速度减小 | |
| C. | 地球同步卫星只能定点在赤道上空,相对地面静止不动 | |
| D. | 运行的线速度小于第一宇宙速度 |
11.下列说法不正确的是( )
| A. | 物体吸收一定频率的电磁波,可能辐射不同频率的电磁波 | |
| B. | 放射性元素的半衰期与原子所处的物理、化学状态有关 | |
| C. | 结合能越大,原子核中的核子结合得越牢固,原子核越稳定 | |
| D. | 铀裂变反应中,如果铀块体积不够大,链式反应不能继续 |
8.随着我国登月计划的实施,我国宇航员登上月球已不是梦想.假如我国宇航员登上月球并在月球表面附近以初速度v0竖直向上抛出一个小球,经时间t后回到出发点.已知月球的半径为R,万有引力常量为G,则下列说法正确的是( )
| A. | 月球表面的重力加速度为$\frac{{v}_{0}}{t}$ | |
| B. | 月球的质量为$\frac{{v}_{0}{R}^{2}}{Gt}$ | |
| C. | 宇航员在月球表面附近绕月球做匀速圆周运动的绕行周期为2π$\sqrt{\frac{Rt}{{v}_{0}}}$ | |
| D. | 宇航员在月球表面获得$\sqrt{\frac{2{v}_{0}R}{t}}$的速度就可能离开月球表面围绕月球做圆周运动 |
 趣味运动会上有一个项目是在传送带上完成的.如图,A为传送带的左端点,B为右端点,P的正上方天花板上悬挂一个气球,AB间传送带的长度L=31m,P与A的距离L1=9m,传送带以v0=1m/s的恒定速率向左运动.比赛中,挑战者(视为质点)在A点相对地面静止,听到硝声后开始以a1=2m/s2的加速度向右匀加速运动到P,在刺破气球时不慎跌倒,经△t=2s爬起,然后又以a2=1m/s2的加速度,在传送带上匀加速到B点.假设从摔倒至爬起的过程中挑战者与传送带始终相对静止,不计刺破气球的时间,求挑战者从A到达B所需的时间.
趣味运动会上有一个项目是在传送带上完成的.如图,A为传送带的左端点,B为右端点,P的正上方天花板上悬挂一个气球,AB间传送带的长度L=31m,P与A的距离L1=9m,传送带以v0=1m/s的恒定速率向左运动.比赛中,挑战者(视为质点)在A点相对地面静止,听到硝声后开始以a1=2m/s2的加速度向右匀加速运动到P,在刺破气球时不慎跌倒,经△t=2s爬起,然后又以a2=1m/s2的加速度,在传送带上匀加速到B点.假设从摔倒至爬起的过程中挑战者与传送带始终相对静止,不计刺破气球的时间,求挑战者从A到达B所需的时间.


