题目内容
11. 如图所示,一直立气缸由两个横截面积不同的长度足够长的圆筒连接而成,活塞A、B间封闭有一定质量的理想气体,A的上方和B的下方分别与大气相通.两活塞用长为L=30cm的不可伸长的质量可忽略不计的细线相连,可在缸内无摩擦地上下滑动.当缸内封闭气体的温度为T1=600K时,活塞A、B的平衡位置如图所示.已知活塞A、B的质量均为m=1.0kg,横截面积分别为SA=20cm2、SB=10cm2,大气压强为p0=1.0×105 Pa,重力加速度为g=10m/s2.
如图所示,一直立气缸由两个横截面积不同的长度足够长的圆筒连接而成,活塞A、B间封闭有一定质量的理想气体,A的上方和B的下方分别与大气相通.两活塞用长为L=30cm的不可伸长的质量可忽略不计的细线相连,可在缸内无摩擦地上下滑动.当缸内封闭气体的温度为T1=600K时,活塞A、B的平衡位置如图所示.已知活塞A、B的质量均为m=1.0kg,横截面积分别为SA=20cm2、SB=10cm2,大气压强为p0=1.0×105 Pa,重力加速度为g=10m/s2.①活塞A、B在图示位置时,求缸内封闭气体的压强;
②现使缸内封闭气体温度缓慢降到300K,求此时气体的体积和压强.
分析 ①分别以两只活塞为研究对象,然后根据平衡条件分别列式,求出初态时封闭气体的压强.
②现对缸内封闭气体缓慢降温过程,先根据盖吕萨克定律,求出A恰好做等压变化,向下运动15cm时的温度,再与300K做比较,判断出是否存在等容过程,再根据过程选择合适的气体定律求解即可.
解答 解:①活塞A、B在题图示位置时,设气缸内气体的压强为p1,以活塞A、B为研究对象,
根据受力平衡可得:p0SA+p1SB+2mg=p0SB+p1SA
解得:p1=p0+$\frac{2mg}{{S}_{A}-{S}_{B}}$=1.2×105Pa
②缓慢降温则活塞向下移动,此过程为等压过程,设当A活塞刚接触气缸时的温度为T2,
体积:V1=$\frac{L}{2}$(SA+SB)=450cm3,V2=LSB=300cm3
温度:T1=600K
封闭气体做等压变化,根据盖-吕萨克定律可得:$\frac{{V}_{1}}{{T}_{1}}$=$\frac{{V}_{2}}{{T}_{2}}$
解得:T2=400K>300K
所以继续降温体积不变,最后体积为300cm3
设最后的压强为p,等容变化,根据查理定律可得:$\frac{{p}_{1}}{{T}_{2}}$=$\frac{p}{{T}_{3}}$
其中T3=300K,代入数据解得压强:p=9×104Pa
答:①活塞A、B在图示位置时,缸内封闭气体的压强为1.2×105Pa;
②现使缸内封闭气体温度缓慢降到300K,此时气体的体积为300cm3,压强为9×104Pa.
点评 本题考查气体定律的综合运用,解题关键是要明确封闭气体的初末状态,然后结合气体实验定律列式求解;同时要对活塞和杆整体受力分析或分别受力分析并结合平衡条件求解初始气压,第②问要注意分析判断温度降到300K时,整体是否向下运动超过15cm.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案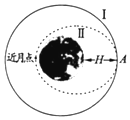 我国将于今年12月发射“嫦娥五号”卫星,该卫星将首次实现在月球上取样并返回地球.如图所示,设“嫦娥五号”先在距月球表面高度为H处的环月轨道I上做运行周期为T的匀速圆周运动;随后在该轨道上的A点采取措施,降至近月点离月球表面高度为h的椭圆轨道Ⅱ上.若以R表示月球半径,忽略月球自转及地球对卫星的影响,已知引力常量G.则下述判断正确的是( )
我国将于今年12月发射“嫦娥五号”卫星,该卫星将首次实现在月球上取样并返回地球.如图所示,设“嫦娥五号”先在距月球表面高度为H处的环月轨道I上做运行周期为T的匀速圆周运动;随后在该轨道上的A点采取措施,降至近月点离月球表面高度为h的椭圆轨道Ⅱ上.若以R表示月球半径,忽略月球自转及地球对卫星的影响,已知引力常量G.则下述判断正确的是( )| A. | “嫦娥五号”在轨道I上A点的加速度大于在轨道Ⅱ上A点的加速度 | |
| B. | “嫦娥五号”在轨道I上A点的速度等于在轨道Ⅱ上A点的速度 | |
| C. | 月球的质量为 $\frac{4{π}^{2}(R+H)^{3}}{G{T}^{2}}$ | |
| D. | “嫦娥五号”在轨道Ⅱ上的周期为$\sqrt{\frac{(2R+H+h)^{3}}{8(R+H)^{3}}}$T |
| A. | 若△t=$\frac{T}{2}$,则在t时刻和(t+△t)时刻弹簧长度一定相等 | |
| B. | 若t时刻和(t+△t)时刻振子运动速度大小相等,方向相反,则△t一定等于$\frac{T}{2}$的整数倍 | |
| C. | 若△t=T,则在t时刻和(t+△t)时刻振子运动的加速度一定相等 | |
| D. | 若t时刻和(t+△t)时刻振子运动位移的大小相等,方向相反,则△t一定等于T的整数倍 |
 如图所示为同一实验室中甲、乙两个单摆的振动图象,从图象中可知( )
如图所示为同一实验室中甲、乙两个单摆的振动图象,从图象中可知( )| A. | 两摆球质量相等 | |
| B. | 两单摆同时改变运动方向 | |
| C. | 两单摆的摆长相等 | |
| D. | 在相同的时间内,两球通过的路程总相等 |

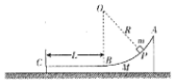 如图所示,一工件置于水平地面上,其AB段为一半径R=1.0m的光滑圆弧轨道,BC段为一长度L=0.5m的粗糙水平轨道,二者相切于B点,整个轨道位于同一竖直平面内,在P点将一个质量m=0.2kg的物块(可视为质点)无初速度释放,物块滑至C点时恰好静止,已知物块与BC段的动摩擦因数μ=0.1,取重力加速度g=10m/s2,求:
如图所示,一工件置于水平地面上,其AB段为一半径R=1.0m的光滑圆弧轨道,BC段为一长度L=0.5m的粗糙水平轨道,二者相切于B点,整个轨道位于同一竖直平面内,在P点将一个质量m=0.2kg的物块(可视为质点)无初速度释放,物块滑至C点时恰好静止,已知物块与BC段的动摩擦因数μ=0.1,取重力加速度g=10m/s2,求: 从受力特点来看,做简谐运动的物体所受到的回复力F=-kx,负号表示回复力F的方向始终与物体偏离平衡位置的位移x的方向相反,k为比例系数.相关文献表明,力学中的-切做简谐运动的物体,其往复运动的周期均可利用公式T=2π$\sqrt{\frac{m}{k}}$求解,m是做简谐运动的物体质量,k为回复力公式中的比例系数.
从受力特点来看,做简谐运动的物体所受到的回复力F=-kx,负号表示回复力F的方向始终与物体偏离平衡位置的位移x的方向相反,k为比例系数.相关文献表明,力学中的-切做简谐运动的物体,其往复运动的周期均可利用公式T=2π$\sqrt{\frac{m}{k}}$求解,m是做简谐运动的物体质量,k为回复力公式中的比例系数. 如图,一内壁光滑、截面恒定、竖直放置的绝热气缸下端密封,上端封闭但留有一出气孔.气缸内部有一绝热活塞,将气缸内的气体(可视为理想气体)分割成上下两部分,气缸底部有一用来加热气体的电阻丝,外界大气压强为 p.当气体温度为 T 时,活塞下方气体的体积为 V,活塞上方气体的体积为 8V;现将气缸水平放置,这一过程温度不变,活塞下方这部分气体的体积变为 2V,此时将出气孔密封.然后重新将气缸竖直放置,并对下部分气体加热.求:
如图,一内壁光滑、截面恒定、竖直放置的绝热气缸下端密封,上端封闭但留有一出气孔.气缸内部有一绝热活塞,将气缸内的气体(可视为理想气体)分割成上下两部分,气缸底部有一用来加热气体的电阻丝,外界大气压强为 p.当气体温度为 T 时,活塞下方气体的体积为 V,活塞上方气体的体积为 8V;现将气缸水平放置,这一过程温度不变,活塞下方这部分气体的体积变为 2V,此时将出气孔密封.然后重新将气缸竖直放置,并对下部分气体加热.求: 如图所示,两端开口、内径均匀的玻璃弯管固定在竖直平面内,两段水银柱A和C将空气柱B封闭在玻璃管左侧,平衡时A段水银有一部分在水平管中.若保持温度不变,向右管缓缓注入少量水银,则再次平衡后,水银柱C两端液面的高度差h将减小,空气柱B的长度将增大.(均选填“增大”、“减小”或“不变”)
如图所示,两端开口、内径均匀的玻璃弯管固定在竖直平面内,两段水银柱A和C将空气柱B封闭在玻璃管左侧,平衡时A段水银有一部分在水平管中.若保持温度不变,向右管缓缓注入少量水银,则再次平衡后,水银柱C两端液面的高度差h将减小,空气柱B的长度将增大.(均选填“增大”、“减小”或“不变”)