题目内容
20. 2014年3月8日凌晨马航客机失联后,西安卫星测控中心紧急调动海洋、风云、高分、遥感4个型号近10颗卫星,为地面搜救提供技术支持.特别是“高分一号”突破了空间分辨率、多光谱与大覆盖面积相结合的大量关键技术.如图为“高分一号”与北斗导航系统两颗卫星在空中某一平面内运动的示意图.“北斗”系统中两颗卫星“G1”和“G3”以及“高分一号”均可认为绕地心O做匀速圆周运动.卫星“G1”和“G3”的轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,“高分一号”在C位置.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则下列说法正确的是( )
2014年3月8日凌晨马航客机失联后,西安卫星测控中心紧急调动海洋、风云、高分、遥感4个型号近10颗卫星,为地面搜救提供技术支持.特别是“高分一号”突破了空间分辨率、多光谱与大覆盖面积相结合的大量关键技术.如图为“高分一号”与北斗导航系统两颗卫星在空中某一平面内运动的示意图.“北斗”系统中两颗卫星“G1”和“G3”以及“高分一号”均可认为绕地心O做匀速圆周运动.卫星“G1”和“G3”的轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,“高分一号”在C位置.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则下列说法正确的是( )| A. | 卫星“G1”和“G3”的加速度大小相等且为$\frac{R}{r}$g | |
| B. | 如果调动“高分一号”卫星快速到达B位置的下方,必须对其加速 | |
| C. | 卫星“G1”由位置A运动到位置B所需的时间为$\frac{πr}{3R}$$\sqrt{\frac{r}{g}}$ | |
| D. | 若“高分一号”所在高度处有稀薄气体,则运行一段时间后,机械能会增大 |
分析 根据万有引力提供向心力和万有引力等于重力求出卫星的加速度和角速度,求出卫星1由位置A运动到位置B的时间.、“高分一号”卫星速度增大,万有引力不够提供向心力,做离心运动,轨道半径变大,速度变小,路程变长,运动时间变长.“高分一号”是低轨道卫星,其所在高度有稀薄气体,要克服阻力做功,机械能减小.
解答 解:A、根据万有引力提供向心力$G\frac{Mm}{{r}^{2}}=ma$得,a=$\frac{GM}{{r}^{2}}$,又GM=gR2,则a=$\frac{g{R}^{2}}{{r}^{2}}$,故A错误.
B、“高分一号”卫星加速,将做离心运动,轨道半径变大,速度变小,路程变长,运动时间变长,故如果调动“高分一号”卫星快速到达B位置的下方,必须对其减速,故B错误.
C、根据万有引力提供向心力$G\frac{Mm}{{r}^{2}}=mr{ω}^{2}$得,$ω=\sqrt{\frac{GM}{{r}^{3}}}$,所以卫星1由位置A运动到位置B所需的时间t=$\frac{\frac{π}{3}}{ω}$=$\frac{πr}{3R}\sqrt{\frac{r}{g}}$,故C正确.
D、“高分一号”是低轨道卫星,其所在高度有稀薄气体,克服阻力做功,机械能减小.故D错误.
故选:C.
点评 解决本题的关键掌握万有引力定律的两个重要理论:1、万有引力等于重力,2、万有引力提供向心力,并能灵活运用.

练习册系列答案
相关题目
11.如图为一物体沿直线运动的速度图象,由此可知( )


| A. | 2s末物体返回出发点 | |
| B. | 4s末物体运动方向改变 | |
| C. | 3s末与5s末的速度大小相等,方向相反 | |
| D. | 8s末物体返回出发点 |
5.天然放射性元素放出的三种射线的穿透能力实验结果如图所示,由此可推知( ) 

| A. | ②来自于原子核外的电子 | |
| B. | ①的电离作用最强,是一种电磁波 | |
| C. | ③照射食品可以杀死腐败的细菌 | |
| D. | ③的电离作用最弱,属于原子核内释放的光子 |
9.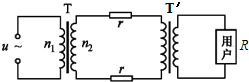 图为远距离输电示意图,两变压器均为理想变压器,升压变压器T的原、副线圈匝数比为k1.降压变压器T′的原、副线圈匝数比k2.原线圈两端接入一电压u=Umsinωt的交流电源,用户电阻为R(纯电阻),若用户消耗功率为P,输电线的总电阻为2r,不考虑其它因素的影响,则输电线上损失的电功率Pr和用户获得的电压U分别为( )
图为远距离输电示意图,两变压器均为理想变压器,升压变压器T的原、副线圈匝数比为k1.降压变压器T′的原、副线圈匝数比k2.原线圈两端接入一电压u=Umsinωt的交流电源,用户电阻为R(纯电阻),若用户消耗功率为P,输电线的总电阻为2r,不考虑其它因素的影响,则输电线上损失的电功率Pr和用户获得的电压U分别为( )
 图为远距离输电示意图,两变压器均为理想变压器,升压变压器T的原、副线圈匝数比为k1.降压变压器T′的原、副线圈匝数比k2.原线圈两端接入一电压u=Umsinωt的交流电源,用户电阻为R(纯电阻),若用户消耗功率为P,输电线的总电阻为2r,不考虑其它因素的影响,则输电线上损失的电功率Pr和用户获得的电压U分别为( )
图为远距离输电示意图,两变压器均为理想变压器,升压变压器T的原、副线圈匝数比为k1.降压变压器T′的原、副线圈匝数比k2.原线圈两端接入一电压u=Umsinωt的交流电源,用户电阻为R(纯电阻),若用户消耗功率为P,输电线的总电阻为2r,不考虑其它因素的影响,则输电线上损失的电功率Pr和用户获得的电压U分别为( )| A. | Pr=$\frac{r}{Rk_2^2}$P $U=(\frac{{\sqrt{2}{k_2}{U_m}}}{{2{k_1}}})(\frac{Rk_2^2}{2r+Rk_2^2})$ | |
| B. | Pr=$\frac{2r}{Rk_2^2}$P $U=(\frac{{\sqrt{2}{U_m}}}{{2{k_1}{k_2}}})(\frac{Rk_2^2}{2r+Rk_2^2})$ | |
| C. | Pr=$\frac{2r}{Rk_2^2}$P $U=(\frac{{\sqrt{2}{k_2}{U_m}}}{{2{k_1}}})(\frac{Rk_2^2}{2r+Rk_2^2})$ | |
| D. | Pr=$\frac{2r}{Rk_1^2}$P $U=(\frac{{\sqrt{2}{U_m}}}{{2{k_1}{k_2}}})(\frac{Rk_2^2}{2r+Rk_2^2})$ |
 如图所示,质量为1kg的物体A从倾角为30°的光滑斜面上由静止开始下滑,(g取10m/s2)问:
如图所示,质量为1kg的物体A从倾角为30°的光滑斜面上由静止开始下滑,(g取10m/s2)问:
 如图所示,是用频闪照相机拍摄到的一小球做平抛运动的闪光照片的一部分,图中方格的边长均为l=5cm,如果取g=10m/s2,那么:
如图所示,是用频闪照相机拍摄到的一小球做平抛运动的闪光照片的一部分,图中方格的边长均为l=5cm,如果取g=10m/s2,那么: 足够长的光滑水平面上有一质量为6kg的处于静止的木板M,停在M的右端的物块N质量为6kg,M、N间的动摩擦因数μ=0.1,用长l=0.8m的轻绳系一质量为m=1kg的小球悬挂在固定点O上,物块N与小球可视为质点,将轻绳拉直至水平位置后,由静止释放小球,小球在最低点与N发生碰撞后反弹,反弹所能达到的最大高度为h=0.2m,同时N获得1m/s的速度,不计空气阻力,g=10m/s2.求:
足够长的光滑水平面上有一质量为6kg的处于静止的木板M,停在M的右端的物块N质量为6kg,M、N间的动摩擦因数μ=0.1,用长l=0.8m的轻绳系一质量为m=1kg的小球悬挂在固定点O上,物块N与小球可视为质点,将轻绳拉直至水平位置后,由静止释放小球,小球在最低点与N发生碰撞后反弹,反弹所能达到的最大高度为h=0.2m,同时N获得1m/s的速度,不计空气阻力,g=10m/s2.求: