题目内容
1．
如图，轻弹簧上端与一质量为m的木块1相连，下端与另一质量为M的木块2相连，整个系统置于水平放置的光滑木坂上，并处于静止状态．现将木板沿水平方向突然抽出，设抽出后的瞬间，木块1、2的加速度大小分别为a1、a2，重力加速度大小为g．则有（ ）| A． | a1=0，a2=g | B． | a1=g，a2=g | C． | a1=0，a2＞g | D． | a1=g，a2＜g |
分析 通过共点力平衡求出弹簧的弹力大小，抓住抽出木板的瞬间，弹簧弹力不变，根据牛顿第二定律求出木块1、2的加速度．
解答 解：对1分析，弹簧的弹力F=mg．
撤去木板的瞬间，弹簧的弹力不变，木块1所受的合力仍然为零，则加速度a1=0．
对木块2，根据牛顿第二定律得，${a}_{2}=\frac{F+Mg}{M}=\frac{m+M}{M}g$．故a2＞g
故选：C．
点评 本题考查了牛顿第二定律的瞬时问题，抓住瞬间弹簧的弹力不变，结合牛顿第二定律进行求解．
练习册系列答案
名题金卷系列答案
相关题目
如图所示，一水平传送装置有轮半径均为R=$\frac{1}{π}$ m的主动轮O1和从动轮O2及传送带等构成．两轮轴心相距8.0m，轮与传送带不打滑．现用此装置运送一袋面粉，已知这袋面粉与传送带之间的动摩擦因数为μ=0.4，这袋面粉中的面粉可不断地从袋中渗出．（g取10m/s2）
17．
如图所示电路中L1发光，L2、L3不亮，
有读数，
没有读数，则产生的故障应是（ ）（只有一处有故障）
如图所示电路中L1发光，L2、L3不亮，有读数，没有读数，则产生的故障应是（ ）（只有一处有故障）| A． | 灯泡L1断路 | B． | 灯泡L2断路 | C． | 灯泡L3短路 | D． | 灯泡L2短路 |
4．
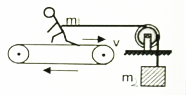如图所示的装置是运动员负重奔跑的跑步机，已知人的质量为m1，绳拴在腰间沿水平方向跨过滑轮（不计滑轮摩擦、质量）悬挂质量为m2的重物，人用力向后蹬使传送带以速率V转动（设人的重心相对地面不动），下面说法正确的是（ ）
如图所示的装置是运动员负重奔跑的跑步机，已知人的质量为m1，绳拴在腰间沿水平方向跨过滑轮（不计滑轮摩擦、质量）悬挂质量为m2的重物，人用力向后蹬使传送带以速率V转动（设人的重心相对地面不动），下面说法正确的是（ ）| A． | 人对重物做功的功率为m2gv | |
| B． | 人对传送带的摩擦力大小等于m2g，方向水平向右 | |
| C． | 人对传送带做功的功率为m2gv | |
| D． | 若增大传送带的速度，人对传送带做功的功率不变 |
6．在下列运动状态中，物体处于平衡状态的有（ ）
| A． | 正在自由下落过程中的石块 | |
| B． | 秋千摆动过程中到达最高点时 | |
| C． | 随传送带一起匀速运动的货物 | |
| D． | 航天员乘坐宇宙飞船进入轨道做圆周运动时 |
如图，有一木板静止在光滑的水平面上，质量为M=4kg，长为L=1.4m．木板的右端放一可视为质点的小木块，质量为m=1kg，两者之间的动摩擦因数为μ=0.4，取g=10m/s2．求：
10．图甲为一列简谐横波在t=0.7s时刻的波形图，图乙为质点P的振动图象，则下列说法正确的是（ ）
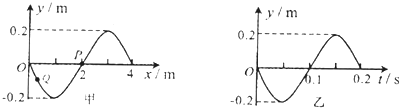
| A． | 波速v=20m/s，向右传播 | |
| B． | 波速v=20m/s，向左传播 | |
| C． | 从t=0.7s时刻开始，再经0.15s，波向左传播了3m | |
| D． | 从t=0.7s时刻开始，再经0.15s，质点P向左运动了3m |
11．
如图所示，质量为M、半径为R的半球形物体A放在水平地面上，通过最高点处的钉子用水平细线拉住一质量为m、半径为r的光滑球B．现整个系统处于静止状态，则（ ）
如图所示，质量为M、半径为R的半球形物体A放在水平地面上，通过最高点处的钉子用水平细线拉住一质量为m、半径为r的光滑球B．现整个系统处于静止状态，则（ ）| A． | A对地面没有摩擦力 | B． | A对地面的摩擦力方向向左 | ||
| C． | B对A的压力大小为$\frac{R+r}{R}$mg | D． | 细线对小球的拉力大小为$\frac{r}{R}$mg |