��Ŀ����
15�� ��ͼ��ʾ������ֱ���µĴŸ�Ӧǿ��ΪB����ǿ�ų��У�������ˮƽ�������ΪL���㹻����ƽ�н�������AB��CD���ڵ����AC������һ��ֵΪR��ĵ��裬һ������Ϊm��ֱ�ڵ�����õĽ�����ab������ΪM������ͨ��һ�������쳤���������Ƶ�ϸ������������ĵ��費�ƣ����뵼��ƽ�У���M�ɾ�ֹ��ʼ�ͷţ�����ֵΪr��ab�������ĵ繦�����ʱ�����ٶ�Ϊ���ab���뵼���Ķ�Ħ������Ϊ�̣�
��ͼ��ʾ������ֱ���µĴŸ�Ӧǿ��ΪB����ǿ�ų��У�������ˮƽ�������ΪL���㹻����ƽ�н�������AB��CD���ڵ����AC������һ��ֵΪR��ĵ��裬һ������Ϊm��ֱ�ڵ�����õĽ�����ab������ΪM������ͨ��һ�������쳤���������Ƶ�ϸ������������ĵ��費�ƣ����뵼��ƽ�У���M�ɾ�ֹ��ʼ�ͷţ�����ֵΪr��ab�������ĵ繦�����ʱ�����ٶ�Ϊ���ab���뵼���Ķ�Ħ������Ϊ�̣�
���� ������ab�Ӿ�ֹ��ʼ�ص��컬�����Ӷ�������Ӧ���������ְ��������������������ٶ���С�ļ����˶������������˶�����ʱab�������ĵ繦�������E=BLv��I=$\frac{E}{R+r}$��F=BIL�Ƶ�����������ʽ����ƽ�������������ٶȣ�
��� �⣺������֪��ab�������˶�ʱ�и�Ÿ��ߣ����������綯�ƣ������ֶ���֪����������ab����ĸ�Ӧ�������������ֶ����֪�������������ܵ��ĺ����ڼ�С�����������ٶ���С�ļ����˶�������������Ħ�����ĺ�������С����Mgʱ������ٶȼ�С��0ʱ���ﵽ����ٶȣ���Ϊv����ʱab�������ĵ繦�����
����Mg=��mg+BIL
����I=$\frac{E}{R+r}$��
E=BLv
��ã�v=$\frac{��M-��m��g��R+r��}{{B}^{2}{L}^{2}}$
�𣺵���ֵΪr��ab�������ĵ繦�����ʱ�����ٶ�Ϊ$\frac{��M-��m��g��R+r��}{{B}^{2}{L}^{2}}$��
���� ����Ҫ����ţ�ٶ��ɷ������������˶�����������ͼ��㰲�����ǹؼ���ע�������ǰ��ܵ�Ħ�������ã�

��ϰ��ϵ�д�
 Сѧ��ĩ���100��ϵ�д�
Сѧ��ĩ���100��ϵ�д� ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д� ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д� �Ƹ�360�ȶ����ܾ�ϵ�д�
�Ƹ�360�ȶ����ܾ�ϵ�д�
�����Ŀ
6�������İ뾶ΪR������Ϊm�������ھ����3R�ߴ��Ƶ���������Բ���˶�����֪���洦���������ٶ�Ϊg��������
| A�� | ���ǵ����ٶ�Ϊ$\sqrt{\frac{gR}{3}}$ | B�� | ���ǵĽ��ٶ�Ϊ $\sqrt{\frac{g}{64R}}$ | ||
| C�� | ���ǵļ��ٶ�Ϊ$\frac{g}{16}$ | D�� | ���ǵ�����Ϊ2��$\sqrt{\frac{64R}{g}}$ |
3��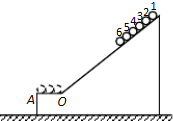 б�����Ͽ��а��ۣ����ڽ������������뾶��Ϊr����ͬ����С��������ͼ��б����ˮƽ���OAƽ�����ӣ�OA����Ϊ6r���ֽ�����С���ɾ�ֹͬʱ�ͷţ�С���뿪A������ƽ���˶�������һ��Ħ�������ڸ�С���˶������У�����˵����ȷ���ǣ�������
б�����Ͽ��а��ۣ����ڽ������������뾶��Ϊr����ͬ����С��������ͼ��б����ˮƽ���OAƽ�����ӣ�OA����Ϊ6r���ֽ�����С���ɾ�ֹͬʱ�ͷţ�С���뿪A������ƽ���˶�������һ��Ħ�������ڸ�С���˶������У�����˵����ȷ���ǣ�������
 б�����Ͽ��а��ۣ����ڽ������������뾶��Ϊr����ͬ����С��������ͼ��б����ˮƽ���OAƽ�����ӣ�OA����Ϊ6r���ֽ�����С���ɾ�ֹͬʱ�ͷţ�С���뿪A������ƽ���˶�������һ��Ħ�������ڸ�С���˶������У�����˵����ȷ���ǣ�������
б�����Ͽ��а��ۣ����ڽ������������뾶��Ϊr����ͬ����С��������ͼ��б����ˮƽ���OAƽ�����ӣ�OA����Ϊ6r���ֽ�����С���ɾ�ֹͬʱ�ͷţ�С���뿪A������ƽ���˶�������һ��Ħ�������ڸ�С���˶������У�����˵����ȷ���ǣ�������| A�� | ��6�Ļ�е���غ� | B�� | ��6��OA�λ�е������ | ||
| C�� | ��6��ˮƽ������ | D�� | ����������ص�λ����ͬ |
20����һ����Ϊ0.2m��ֱ������ͨ��2A�ĵ����������߷�����ǿ�ų��У��ܵ��İ�����Ϊ0.2N������ǿ�ų��ĴŸ�Ӧǿ�ȵĴ�С�����ǣ�������
| A�� | 0.8T | B�� | 0.4T | C�� | 0.2T | D�� | 0.1T |
17�� ��ͼ��ʾ�����߹�CD�ĵ����Ʒ�������������AB�������߹�ʱ����·����ͼʾ����ĸ�Ӧ�������������й������߹�C�˼��Ե��жϣ���ȷ���ǣ�������
��ͼ��ʾ�����߹�CD�ĵ����Ʒ�������������AB�������߹�ʱ����·����ͼʾ����ĸ�Ӧ�������������й������߹�C�˼��Ե��жϣ���ȷ���ǣ�������
 ��ͼ��ʾ�����߹�CD�ĵ����Ʒ�������������AB�������߹�ʱ����·����ͼʾ����ĸ�Ӧ�������������й������߹�C�˼��Ե��жϣ���ȷ���ǣ�������
��ͼ��ʾ�����߹�CD�ĵ����Ʒ�������������AB�������߹�ʱ����·����ͼʾ����ĸ�Ӧ�������������й������߹�C�˼��Ե��жϣ���ȷ���ǣ�������| A�� | C��һ����N�� | |
| B�� | C��һ����S�� | |
| C�� | C�˵ļ���һ�������B�˵ļ�����ͬ | |
| D�� | ���жϼ��ԣ������߹ܵ��Ʒ����� |

 ��ͼ��ʾ��б�泤5cm����1cm��������600N������б�����2400N�����������Ƶ����ϣ��������������Ĺ���3000J��б��Ļ�еЧ����60%��
��ͼ��ʾ��б�泤5cm����1cm��������600N������б�����2400N�����������Ƶ����ϣ��������������Ĺ���3000J��б��Ļ�еЧ����60%�� ��ͼ��ʾ���ʵ��A�㿪ʼ�ذ뾶r=20cm��Բ��˳ʱ�뷽��������Բ���˶������ٶ�Ϊ��=$\frac{��}{3}$rad/s�����ʱ�䣬�ʵ��λ�ƴ�СΪ20cm��
��ͼ��ʾ���ʵ��A�㿪ʼ�ذ뾶r=20cm��Բ��˳ʱ�뷽��������Բ���˶������ٶ�Ϊ��=$\frac{��}{3}$rad/s�����ʱ�䣬�ʵ��λ�ƴ�СΪ20cm��