题目内容
19.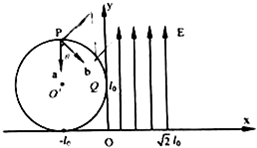 如图所示,在xoy坐标系第二象限内有一圆形匀强磁场区域,半径为l0,圆心O′坐标为(-l0,l0),磁场方向垂直xoy平面.在坐标(-l0,2l0)的P点,两个电子a、b以相同的速率v沿不同方向从P点同时射入磁场,电子a的入射方向为y轴负方向,b的入射方向与y轴负方向夹角为θ=45°.电子a经过磁场偏转后从y轴上的 Q(0,l0)点进入第一象限,在第一象限内紧邻y轴有沿y轴正方向的匀强电场,场强大小为$\frac{m{v}^{2}}{e{l}_{0}}$,匀强电场宽为$\sqrt{2}$l0.已知电子质量为m、电荷量为e,不计重力及电子间的相互作用.求:
如图所示,在xoy坐标系第二象限内有一圆形匀强磁场区域,半径为l0,圆心O′坐标为(-l0,l0),磁场方向垂直xoy平面.在坐标(-l0,2l0)的P点,两个电子a、b以相同的速率v沿不同方向从P点同时射入磁场,电子a的入射方向为y轴负方向,b的入射方向与y轴负方向夹角为θ=45°.电子a经过磁场偏转后从y轴上的 Q(0,l0)点进入第一象限,在第一象限内紧邻y轴有沿y轴正方向的匀强电场,场强大小为$\frac{m{v}^{2}}{e{l}_{0}}$,匀强电场宽为$\sqrt{2}$l0.已知电子质量为m、电荷量为e,不计重力及电子间的相互作用.求:(1)磁场的磁感应强度B的大小
(2)a、b两个电子经过电场后到达x轴的坐标差△x
(3)a、b两个电子从P点运动到达x轴的时间差△t.
分析 (1)带电粒子在磁场中做匀速圆周运动,由几何关系可知电子的运动半径,由洛仑兹力充当向心力可求得磁感应强度B;
(2)电子在电场中做类平抛运动,其中b粒子离开电场后做直线运动,由运动学规律可求得两电子到达x轴上的坐标值,进而求得坐标差
(3)分别求出两电子在磁场和电场中的时间,即可求得两电子从P运动到x轴的时间差.
解答 解:(1)
两电子轨道如图 ,有图可知,a电子做圆周圆周运动的半径为R=l0
,有图可知,a电子做圆周圆周运动的半径为R=l0
$Bve=m\frac{{v}^{2}}{R}$
解得B=$\frac{mv}{e{l}_{0}}$
(2)a在电场中$y=\frac{1}{2}{at}_{1}^{2}$
$a=\frac{eE}{m}$
$\sqrt{2}{l}_{0}=v{t}_{2}$
可得y=l0,即a电子恰好击中x轴上的$\sqrt{2}{l}_{0}$位置,
对b分析可知PO′NO″为菱形,所以PO′与O″N平行,有因PO′垂直于x轴,所以粒子出场速度平行于x轴,即b粒子经过磁场偏转后也恰好沿x轴正方向进入电场
由${y}_{b}=r+rcos45°={l}_{0}+\frac{\sqrt{2}}{2}{l}_{0}$
当b在电场中沿y方向运动l0后,沿与x轴方向成θ做匀速直线运动,
tan$θ=\frac{{v}_{y}}{v}$
vy=at1
由tan$θ=\sqrt{2}$
可得$tanθ=\frac{{y}_{b}-{y}_{a}}{△x}$
解得$△x=\frac{{l}_{0}}{2}$
(3)在磁场中,由t=$\frac{2π{l}_{0}}{v}$
ab在磁场中运动的时间差为△t1
$\frac{△{t}_{1}}{T}=\frac{△θ}{2π}$
$△θ=\frac{π}{2}-\frac{π}{4}=\frac{π}{4}$
$△{t}_{1}=\frac{T}{8}$
所以$△{t}_{1}=\frac{π{l}_{0}}{4v}$
b在第二象限内无场区域的匀速运动时间为△t2
$△{t}_{2}=\frac{r-rcos45°}{v}=\frac{(1-\frac{\sqrt{2}}{2}){l}_{0}}{v}$
ab在第一象限内运动的时间差为$△{t}_{3}=\frac{△x}{v}=\frac{{l}_{0}}{2v}$
所以时间差为$△t=△{t}_{1}+△{t}_{2}+△{t}_{3}=\frac{{l}_{0}}{4}(6-π-2\sqrt{2})$
答:(1)磁场的磁感应强度B的大小$\frac{mv}{e{l}_{0}}$
(2)a、b两个电子经过电场后到达x轴的坐标差△x$\frac{{l}_{0}}{2}$
(3)a、b两个电子从P点运动到达x轴的时间差△t$\frac{{l}_{0}}{4}(6-π-2\sqrt{2})$
点评 本题考查带电粒子在磁场和电场中的运动,要注意电子在磁场中做匀速圆周运动,在磁场中做平抛运动,要求正确利用好几何关系进行分析.

 名校课堂系列答案
名校课堂系列答案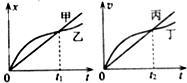 如图所示的x-t图象和v-t图象中给出了四条图线甲、乙、丙、丁,他们分别描述了四辆车由同一地点向同一方向的运动情况,则下列说法正确的是( )
如图所示的x-t图象和v-t图象中给出了四条图线甲、乙、丙、丁,他们分别描述了四辆车由同一地点向同一方向的运动情况,则下列说法正确的是( )| A. | 甲车做匀加速直线运动,乙车做变加速直线运动 | |
| B. | 0-t1时间内,甲乙两车通过的位移相等 | |
| C. | 0-t2时间内,丙、丁两车在t2时刻相距最远 | |
| D. | 0-t2时间内,丙车的平均速度大于丁车的平均速度 |
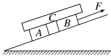 如图所示,三个物块A、B、C叠放在斜面上,用方向与斜面平行的拉力F作用在B上,使三个物块一起沿斜面向上做匀速运动.设物块C对A的摩擦力为fA,对B的摩擦力为fB,下列说法正确的是( )
如图所示,三个物块A、B、C叠放在斜面上,用方向与斜面平行的拉力F作用在B上,使三个物块一起沿斜面向上做匀速运动.设物块C对A的摩擦力为fA,对B的摩擦力为fB,下列说法正确的是( )| A. | 如果斜面光滑,fA与fB方向相反,且fA<fB | |
| B. | 如果斜面光滑,fA与fB方向相同,且fA>fB | |
| C. | 如果斜面粗糙,fA与fB方向相同,且fA>fB | |
| D. | 如果斜面粗糙,fA与fB方向相反,且fA<fB |
 轻绳一端系在质量为m的物体A上,另一端系在一个套在粗糙竖直杆MN的圆环上,在水平力F作用下,物体A从图中实线位置缓慢下降到虚线位置,但圆环仍保持在原来位置不动,则在这一过程中,环对杆的摩擦力F1和环对杆的压力F2的变化情况是( )
轻绳一端系在质量为m的物体A上,另一端系在一个套在粗糙竖直杆MN的圆环上,在水平力F作用下,物体A从图中实线位置缓慢下降到虚线位置,但圆环仍保持在原来位置不动,则在这一过程中,环对杆的摩擦力F1和环对杆的压力F2的变化情况是( )| A. | F1保持不变,F2逐渐减小 | B. | F1逐渐增大,F2保持不变 | ||
| C. | F1逐渐减小,F2保持不变 | D. | F1保持不变,F2逐渐增大 |
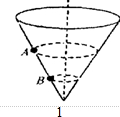 如图所示.固定的圆锥圆筒内壁光滑,壁上有两个小球A和B各自在不同高度的水平面内做匀速圆周运动,已知两小球质量为mA=2mB,则可以判定它们对壁筒的压力FN以及它们的线速度v、角速度ω和向心加速度a的大小关系应由( )
如图所示.固定的圆锥圆筒内壁光滑,壁上有两个小球A和B各自在不同高度的水平面内做匀速圆周运动,已知两小球质量为mA=2mB,则可以判定它们对壁筒的压力FN以及它们的线速度v、角速度ω和向心加速度a的大小关系应由( )| A. | vA>vB | B. | ωA>ωB | C. | aA>aB | D. | FNA>FNB |
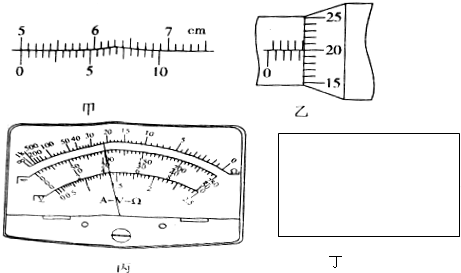

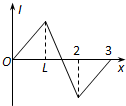
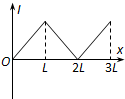
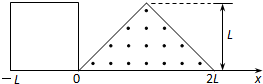 如图所示,等腰三角形内分布有垂直于纸面向外的匀强磁场,它的底边在x轴上且长为2L,高为L,纸面内一边长为L的正方形导线框沿x轴正方向做匀速直线运动穿过匀强磁场区域,在t=0时刻恰好位于如图所示的位置,以顺时针方向为导线框中电流的正方向,下面四幅图中能够正确表示导线框中的电流-位移(I-x)关系的是( )
如图所示,等腰三角形内分布有垂直于纸面向外的匀强磁场,它的底边在x轴上且长为2L,高为L,纸面内一边长为L的正方形导线框沿x轴正方向做匀速直线运动穿过匀强磁场区域,在t=0时刻恰好位于如图所示的位置,以顺时针方向为导线框中电流的正方向,下面四幅图中能够正确表示导线框中的电流-位移(I-x)关系的是( )

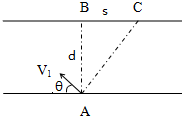 如图所示,一只小船从河岸A点出发,船头垂直于河岸行驶,经时间t到达距正对岸下游s处的C点.若小船速度不变,保持船身轴线与河岸成某夹角行驶,经过$\frac{5}{4}t$到达正对岸B点,则此河的宽度d为多少?
如图所示,一只小船从河岸A点出发,船头垂直于河岸行驶,经时间t到达距正对岸下游s处的C点.若小船速度不变,保持船身轴线与河岸成某夹角行驶,经过$\frac{5}{4}t$到达正对岸B点,则此河的宽度d为多少?