题目内容
8.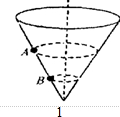 如图所示.固定的圆锥圆筒内壁光滑,壁上有两个小球A和B各自在不同高度的水平面内做匀速圆周运动,已知两小球质量为mA=2mB,则可以判定它们对壁筒的压力FN以及它们的线速度v、角速度ω和向心加速度a的大小关系应由( )
如图所示.固定的圆锥圆筒内壁光滑,壁上有两个小球A和B各自在不同高度的水平面内做匀速圆周运动,已知两小球质量为mA=2mB,则可以判定它们对壁筒的压力FN以及它们的线速度v、角速度ω和向心加速度a的大小关系应由( )| A. | vA>vB | B. | ωA>ωB | C. | aA>aB | D. | FNA>FNB |
分析 小球做匀速圆周运动,由合外力提供向心力,对物体正确进行受力分析,然后根据向心力公式列方程求解即可.
解答  解:A、设漏斗内壁母线与水平方向的夹角为θ.
解:A、设漏斗内壁母线与水平方向的夹角为θ.
以任意一个小球为研究对象,分析受力情况:重力mg和漏斗内壁的支持力N,它们的合力提供向心力,如图.
则根据牛顿第二定律得:
mgtanθ=m$\frac{{v}^{2}}{r}$,
得:v=$\sqrt{grtanθ}$,θ一定,则v与$\sqrt{r}$成正比,A球的圆周运动半径大于B球的圆周运动,所以vA>vB,故A正确;
B、角速度ω=$\frac{v}{r}$=$\sqrt{\frac{gtanθ}{r}}$,则角速度ω与$\sqrt{r}$成反比,A球的圆周运动半径大于B球的圆周运动,所以角速度ωA<ωB,故B错误;
C、向心加速度为:a=$\frac{{v}^{2}}{r}$=gtanθ,与半径r无关,故aA=aB,故C错误;
D、漏斗内壁的支持力为:FN=$\frac{mg}{cosθ}$,θ相同,mA=2mB,则FNA>FNB,故D正确;
故选:AD.
点评 解决这类圆周运动问题的关键是对物体正确受力分析,根据向心力公式列方程进行讨论,注意各种向心加速度表达式的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 如图所示,A是一个质量为M的盒子,B的质量为m,A、B用细绳相连,跨过光滑的定滑轮,A置于倾角为θ的斜面上,B悬于斜面之外处于静止状态,若向A中缓慢加入沙子,整个系统保持静止,则在加入沙子的过程中( )
如图所示,A是一个质量为M的盒子,B的质量为m,A、B用细绳相连,跨过光滑的定滑轮,A置于倾角为θ的斜面上,B悬于斜面之外处于静止状态,若向A中缓慢加入沙子,整个系统保持静止,则在加入沙子的过程中( )
 如图所示,A是一个质量为M的盒子,B的质量为m,A、B用细绳相连,跨过光滑的定滑轮,A置于倾角为θ的斜面上,B悬于斜面之外处于静止状态,若向A中缓慢加入沙子,整个系统保持静止,则在加入沙子的过程中( )
如图所示,A是一个质量为M的盒子,B的质量为m,A、B用细绳相连,跨过光滑的定滑轮,A置于倾角为θ的斜面上,B悬于斜面之外处于静止状态,若向A中缓慢加入沙子,整个系统保持静止,则在加入沙子的过程中( )| A. | 绳子拉力大小不变 | B. | A所受合力逐渐增大 | ||
| C. | A所受摩擦力逐渐增大 | D. | A对斜面压力逐渐增大 |
16. 如图所示,重2N的物体静止在粗糙水平面上,用F=6N的力斜向下推物体,已知F与水平面成30°角,物体与水平面间的动摩擦因数μ=0.5,已知物体与地面间的最大静摩擦力等于滑动摩擦力,则( )
如图所示,重2N的物体静止在粗糙水平面上,用F=6N的力斜向下推物体,已知F与水平面成30°角,物体与水平面间的动摩擦因数μ=0.5,已知物体与地面间的最大静摩擦力等于滑动摩擦力,则( )
 如图所示,重2N的物体静止在粗糙水平面上,用F=6N的力斜向下推物体,已知F与水平面成30°角,物体与水平面间的动摩擦因数μ=0.5,已知物体与地面间的最大静摩擦力等于滑动摩擦力,则( )
如图所示,重2N的物体静止在粗糙水平面上,用F=6N的力斜向下推物体,已知F与水平面成30°角,物体与水平面间的动摩擦因数μ=0.5,已知物体与地面间的最大静摩擦力等于滑动摩擦力,则( )| A. | 物体对地面的压力为5N | B. | 物体所受的摩擦力为1N | ||
| C. | 物体所受的合力为(3$\sqrt{3}$-2.5)N | D. | 物体所受的合力为零 |
13. 如图所示,带正电的电荷固定于点Q,电子在库仑力作用下,做以Q为焦点的椭圆运动,M、P、N为椭圆上的三点,P点是轨道上离Q最近的点,电子在从M经P到达N点的过程中( )
如图所示,带正电的电荷固定于点Q,电子在库仑力作用下,做以Q为焦点的椭圆运动,M、P、N为椭圆上的三点,P点是轨道上离Q最近的点,电子在从M经P到达N点的过程中( )
 如图所示,带正电的电荷固定于点Q,电子在库仑力作用下,做以Q为焦点的椭圆运动,M、P、N为椭圆上的三点,P点是轨道上离Q最近的点,电子在从M经P到达N点的过程中( )
如图所示,带正电的电荷固定于点Q,电子在库仑力作用下,做以Q为焦点的椭圆运动,M、P、N为椭圆上的三点,P点是轨道上离Q最近的点,电子在从M经P到达N点的过程中( )| A. | 速率先增大后减小 | B. | 速率先减小后增大 | ||
| C. | 电势能先减小后增大 | D. | 电势能先增大后减小 |
20. 有一秒摆悬点为O,在O点正下方O′处有一钉子,如图甲所示,摆从平衡位置向左摆时摆线碰到钉子,摆长改变,从平衡位置向右摆时又变为原摆的长度,其振动图象如图乙所示(g=π2),则( )
有一秒摆悬点为O,在O点正下方O′处有一钉子,如图甲所示,摆从平衡位置向左摆时摆线碰到钉子,摆长改变,从平衡位置向右摆时又变为原摆的长度,其振动图象如图乙所示(g=π2),则( )
 有一秒摆悬点为O,在O点正下方O′处有一钉子,如图甲所示,摆从平衡位置向左摆时摆线碰到钉子,摆长改变,从平衡位置向右摆时又变为原摆的长度,其振动图象如图乙所示(g=π2),则( )
有一秒摆悬点为O,在O点正下方O′处有一钉子,如图甲所示,摆从平衡位置向左摆时摆线碰到钉子,摆长改变,从平衡位置向右摆时又变为原摆的长度,其振动图象如图乙所示(g=π2),则( )| A. | 此摆的周期为2s | |
| B. | 悬点离钉子的距离为0.75m | |
| C. | 碰到钉子瞬间,摆球的速度大小不变 | |
| D. | 碰钉子后,摆球的角速度增大 |
12.用水平力F将木块M紧压在竖直的墙壁上,若以N表示墙壁对木块的弹力,R表示木块对墙壁的压力,下列对F、N、R判断中正确的是( )
| A. | N和F的合力为零 | B. | F和N是一对平衡力 | ||
| C. | R和N是作用力和反作用力 | D. | N和R是性质不同的力 |
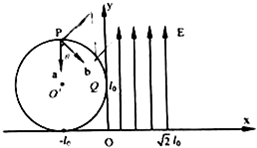 如图所示,在xoy坐标系第二象限内有一圆形匀强磁场区域,半径为l0,圆心O′坐标为(-l0,l0),磁场方向垂直xoy平面.在坐标(-l0,2l0)的P点,两个电子a、b以相同的速率v沿不同方向从P点同时射入磁场,电子a的入射方向为y轴负方向,b的入射方向与y轴负方向夹角为θ=45°.电子a经过磁场偏转后从y轴上的 Q(0,l0)点进入第一象限,在第一象限内紧邻y轴有沿y轴正方向的匀强电场,场强大小为$\frac{m{v}^{2}}{e{l}_{0}}$,匀强电场宽为$\sqrt{2}$l0.已知电子质量为m、电荷量为e,不计重力及电子间的相互作用.求:
如图所示,在xoy坐标系第二象限内有一圆形匀强磁场区域,半径为l0,圆心O′坐标为(-l0,l0),磁场方向垂直xoy平面.在坐标(-l0,2l0)的P点,两个电子a、b以相同的速率v沿不同方向从P点同时射入磁场,电子a的入射方向为y轴负方向,b的入射方向与y轴负方向夹角为θ=45°.电子a经过磁场偏转后从y轴上的 Q(0,l0)点进入第一象限,在第一象限内紧邻y轴有沿y轴正方向的匀强电场,场强大小为$\frac{m{v}^{2}}{e{l}_{0}}$,匀强电场宽为$\sqrt{2}$l0.已知电子质量为m、电荷量为e,不计重力及电子间的相互作用.求:
 如图所示是一种测量血压的压力传感器在工作时的示意图.薄金属片P固定有4个可以形变的电阻R1、R2、R3、R4,如图(乙),图(甲)是它的侧面图,这4个电阻连成的电路如图(丙)所示.试回答下列问题:
如图所示是一种测量血压的压力传感器在工作时的示意图.薄金属片P固定有4个可以形变的电阻R1、R2、R3、R4,如图(乙),图(甲)是它的侧面图,这4个电阻连成的电路如图(丙)所示.试回答下列问题: