题目内容
9.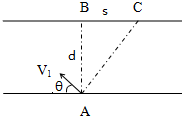 如图所示,一只小船从河岸A点出发,船头垂直于河岸行驶,经时间t到达距正对岸下游s处的C点.若小船速度不变,保持船身轴线与河岸成某夹角行驶,经过$\frac{5}{4}t$到达正对岸B点,则此河的宽度d为多少?
如图所示,一只小船从河岸A点出发,船头垂直于河岸行驶,经时间t到达距正对岸下游s处的C点.若小船速度不变,保持船身轴线与河岸成某夹角行驶,经过$\frac{5}{4}t$到达正对岸B点,则此河的宽度d为多少?
分析 将小船的运动分解为沿河岸方向和垂直于河岸方向,抓住分运动与合运动具有等时性,可以求出水流速度与小艇在静水中的速度,从而可求出河的宽度.
解答 解:设水流速度为v1,小艇在静水中速度为v2,
小艇身与河岸垂直时,s=v1t,则有:v1=$\frac{s}{t}$;
小艇保持原来的速度逆水斜向上游与河岸成的θ角,恰好到达正对岸的B处,
则有:d=$\sqrt{{v}_{2}^{2}-{v}_{1}^{2}}$$\frac{5}{4}$t,小艇身与河岸垂直时,d=v2t,
解得:v2=;
由上分析可知,河宽d=v2t=$\frac{\sqrt{16{d}^{2}+25{s}^{2}}}{5}$;
答:河宽为$\frac{\sqrt{16{d}^{2}+25{s}^{2}}}{5}$.
点评 解决本题的关键知道分运动和合运动具有等时性,以及会根据平行四边形定则对运动进行合成和分解.

练习册系列答案
相关题目
20. 有一秒摆悬点为O,在O点正下方O′处有一钉子,如图甲所示,摆从平衡位置向左摆时摆线碰到钉子,摆长改变,从平衡位置向右摆时又变为原摆的长度,其振动图象如图乙所示(g=π2),则( )
有一秒摆悬点为O,在O点正下方O′处有一钉子,如图甲所示,摆从平衡位置向左摆时摆线碰到钉子,摆长改变,从平衡位置向右摆时又变为原摆的长度,其振动图象如图乙所示(g=π2),则( )
 有一秒摆悬点为O,在O点正下方O′处有一钉子,如图甲所示,摆从平衡位置向左摆时摆线碰到钉子,摆长改变,从平衡位置向右摆时又变为原摆的长度,其振动图象如图乙所示(g=π2),则( )
有一秒摆悬点为O,在O点正下方O′处有一钉子,如图甲所示,摆从平衡位置向左摆时摆线碰到钉子,摆长改变,从平衡位置向右摆时又变为原摆的长度,其振动图象如图乙所示(g=π2),则( )| A. | 此摆的周期为2s | |
| B. | 悬点离钉子的距离为0.75m | |
| C. | 碰到钉子瞬间,摆球的速度大小不变 | |
| D. | 碰钉子后,摆球的角速度增大 |
4.关于两个物体间作用力与反作用力,下列说法中不正确的是( )
| A. | 作用力与反作用力的性质一定相同 | |
| B. | 只有两个物体处于平衡状态中,作用力与反作用力才大小相等 | |
| C. | 作用力与反作用力不一定沿着同一直线 | |
| D. | 有作用力才有反作用力,因此先有作用力后产生反作用力 |
12.用水平力F将木块M紧压在竖直的墙壁上,若以N表示墙壁对木块的弹力,R表示木块对墙壁的压力,下列对F、N、R判断中正确的是( )
| A. | N和F的合力为零 | B. | F和N是一对平衡力 | ||
| C. | R和N是作用力和反作用力 | D. | N和R是性质不同的力 |
13. 如图所示,真空中有一均匀玻璃球,虚线CD过球心O.两束单色光Ⅰ、Ⅱ分别由玻璃球表面上的A、B两点折射进入玻璃球,Ⅰ从D点射出,Ⅱ从E点射出(图中未画出离开玻璃球后的出射光线),Ⅰ、Ⅱ平行于CD且三线共面,∠AOC=∠BOC=60°,则下列说法正确的是( )
如图所示,真空中有一均匀玻璃球,虚线CD过球心O.两束单色光Ⅰ、Ⅱ分别由玻璃球表面上的A、B两点折射进入玻璃球,Ⅰ从D点射出,Ⅱ从E点射出(图中未画出离开玻璃球后的出射光线),Ⅰ、Ⅱ平行于CD且三线共面,∠AOC=∠BOC=60°,则下列说法正确的是( )
 如图所示,真空中有一均匀玻璃球,虚线CD过球心O.两束单色光Ⅰ、Ⅱ分别由玻璃球表面上的A、B两点折射进入玻璃球,Ⅰ从D点射出,Ⅱ从E点射出(图中未画出离开玻璃球后的出射光线),Ⅰ、Ⅱ平行于CD且三线共面,∠AOC=∠BOC=60°,则下列说法正确的是( )
如图所示,真空中有一均匀玻璃球,虚线CD过球心O.两束单色光Ⅰ、Ⅱ分别由玻璃球表面上的A、B两点折射进入玻璃球,Ⅰ从D点射出,Ⅱ从E点射出(图中未画出离开玻璃球后的出射光线),Ⅰ、Ⅱ平行于CD且三线共面,∠AOC=∠BOC=60°,则下列说法正确的是( )| A. | 玻璃球对Ⅱ光的折射率小于$\sqrt{3}$ | |
| B. | 在玻璃球中,Ⅰ光传播的速度大于II光传播的速度 | |
| C. | 无论怎样改变入射角的大小,进入玻璃球的II光总能射出玻璃球 | |
| D. | 用Ⅰ光与II光照射同一双缝干涉装置,光屏上Ⅰ比Ⅱ的明条纹间距大 |
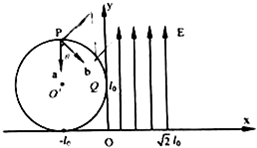 如图所示,在xoy坐标系第二象限内有一圆形匀强磁场区域,半径为l0,圆心O′坐标为(-l0,l0),磁场方向垂直xoy平面.在坐标(-l0,2l0)的P点,两个电子a、b以相同的速率v沿不同方向从P点同时射入磁场,电子a的入射方向为y轴负方向,b的入射方向与y轴负方向夹角为θ=45°.电子a经过磁场偏转后从y轴上的 Q(0,l0)点进入第一象限,在第一象限内紧邻y轴有沿y轴正方向的匀强电场,场强大小为$\frac{m{v}^{2}}{e{l}_{0}}$,匀强电场宽为$\sqrt{2}$l0.已知电子质量为m、电荷量为e,不计重力及电子间的相互作用.求:
如图所示,在xoy坐标系第二象限内有一圆形匀强磁场区域,半径为l0,圆心O′坐标为(-l0,l0),磁场方向垂直xoy平面.在坐标(-l0,2l0)的P点,两个电子a、b以相同的速率v沿不同方向从P点同时射入磁场,电子a的入射方向为y轴负方向,b的入射方向与y轴负方向夹角为θ=45°.电子a经过磁场偏转后从y轴上的 Q(0,l0)点进入第一象限,在第一象限内紧邻y轴有沿y轴正方向的匀强电场,场强大小为$\frac{m{v}^{2}}{e{l}_{0}}$,匀强电场宽为$\sqrt{2}$l0.已知电子质量为m、电荷量为e,不计重力及电子间的相互作用.求: 如图所示是一种测量血压的压力传感器在工作时的示意图.薄金属片P固定有4个可以形变的电阻R1、R2、R3、R4,如图(乙),图(甲)是它的侧面图,这4个电阻连成的电路如图(丙)所示.试回答下列问题:
如图所示是一种测量血压的压力传感器在工作时的示意图.薄金属片P固定有4个可以形变的电阻R1、R2、R3、R4,如图(乙),图(甲)是它的侧面图,这4个电阻连成的电路如图(丙)所示.试回答下列问题: