题目内容
6. 如图所示,质量分别为M和m的物体A和B静止在光滑水平面上,A左侧被很簿的油泥层粘在竖直墙壁上,AB之间用一轻质弹簧相连,现用一水平向右的外力F作用在B上,外力作用一段时间后,A离开墙壁开始运动,此时撤掉外力,且弹簧此时的弹性势能为E1,在以后的运动过程中,弹簧弹性势能的最大值为E2,设外力F对B的冲量为I0,求从静止到A开始运动的过程中A受到油泥层黏力的冲量I的大小.
如图所示,质量分别为M和m的物体A和B静止在光滑水平面上,A左侧被很簿的油泥层粘在竖直墙壁上,AB之间用一轻质弹簧相连,现用一水平向右的外力F作用在B上,外力作用一段时间后,A离开墙壁开始运动,此时撤掉外力,且弹簧此时的弹性势能为E1,在以后的运动过程中,弹簧弹性势能的最大值为E2,设外力F对B的冲量为I0,求从静止到A开始运动的过程中A受到油泥层黏力的冲量I的大小.
分析 弹簧形变量最大时,A、B速度相等,且该过程中系统动量守恒,能量也守恒,结合动量守恒,能量守恒和动量定理求解.
解答 解:设A开始运动前弹簧对B的冲量为I,A开始运动时B的速度为v0,A开始运动前的过程中,对B,根据动量定理得:
I0-I=mv0,
而A开始运动后,到弹簧形变量最大时,A、B速度相等,且该过程中系统动量守恒,能量也守恒,以向右为正方向,由动量守恒定律得:
mv0=(M+m)v,
由能量守恒定律得:$\frac{1}{2}$mv02+E1=$\frac{1}{2}$(M+m)v2+E2,
解得:I=I0-$\sqrt{\frac{2m(M+m)({E}_{2}-{E}_{1})}{M}}$,
而A开始运动前油泥层黏力的冲量与弹簧对A的弹力的冲量大小相等,
则:I′=I=I0-$\sqrt{\frac{2m(M+m)({E}_{2}-{E}_{1})}{M}}$;
答:从静止到A开始运动的过程中A受到油泥层黏力的冲量I的大小为I0-$\sqrt{\frac{2m(M+m)({E}_{2}-{E}_{1})}{M}}$.
点评 本题关键分析清楚两个物体和弹簧系统的运动规律,还要结合机械能守恒定律和动量守恒定律分析,较难.

练习册系列答案
相关题目
11.小球由地面竖直上抛,上升的最大高度为H,地面为零势能面,在上升至离地高度h处,小球的势能是动能的2倍,空气阻力不计,则h等于( )
| A. | $\frac{H}{4}$ | B. | $\frac{H}{3}$ | C. | $\frac{H}{2}$ | D. | $\frac{2H}{3}$ |
18. 用显微镜观察花粉颗粒在水中做布朗运动,如图是每隔30秒记录的花粉颗粒位置图,下列说法正确的是( )
用显微镜观察花粉颗粒在水中做布朗运动,如图是每隔30秒记录的花粉颗粒位置图,下列说法正确的是( )
 用显微镜观察花粉颗粒在水中做布朗运动,如图是每隔30秒记录的花粉颗粒位置图,下列说法正确的是( )
用显微镜观察花粉颗粒在水中做布朗运动,如图是每隔30秒记录的花粉颗粒位置图,下列说法正确的是( )| A. | 图中无规则的连线即为花粉颗粒的运动轨迹 | |
| B. | 每段30秒内连线也不是微粒的运动轨迹 | |
| C. | 悬浮在液体中的微粒越小,受到液体分子的撞击越容易平衡 | |
| D. | 布朗运动的剧烈程度与温度有关,所以布朗运动就是分子的热运动 |
15. 图中的实线表示电场线、虚线表示只受电场力作用的带电粒子的运动轨迹.粒子先经过M点,再经过N点,则可以判定( )
图中的实线表示电场线、虚线表示只受电场力作用的带电粒子的运动轨迹.粒子先经过M点,再经过N点,则可以判定( )
 图中的实线表示电场线、虚线表示只受电场力作用的带电粒子的运动轨迹.粒子先经过M点,再经过N点,则可以判定( )
图中的实线表示电场线、虚线表示只受电场力作用的带电粒子的运动轨迹.粒子先经过M点,再经过N点,则可以判定( )| A. | M点的电势高于N点的电势 | |
| B. | 粒子在M点的电势能小于N点的电势能 | |
| C. | 粒子在M点的加速度大于在N点的加速度 | |
| D. | 粒子在M点的速度小于在N点的速度 |
16.下列物理量不可能为负值的是( )
| A. | 加速度 | B. | 功 | C. | 动能 | D. | 重力势能 |
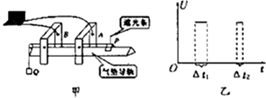 某学习小组利用气垫导轨验证机械能守恒定律,实验装置如图甲所示.当气垫导轨正常工作时导轨两侧喷出的气体使滑块悬浮在导轨上方,滑块与导轨间的阻力可忽略不计.在气垫导轨上相隔一定距离的两处安装两个光电传感器A、B,滑块P上固定一遮光条,若光线被遮光条遮挡,光电传感器会输出高电压,两光电传感器采集数据后与计算机相连.滑块在细线的牵引下向左加速运动,遮光条经过光电传感器A、B时,通过计算机可以得到如图乙所示的电压U随时间t变化的图线.
某学习小组利用气垫导轨验证机械能守恒定律,实验装置如图甲所示.当气垫导轨正常工作时导轨两侧喷出的气体使滑块悬浮在导轨上方,滑块与导轨间的阻力可忽略不计.在气垫导轨上相隔一定距离的两处安装两个光电传感器A、B,滑块P上固定一遮光条,若光线被遮光条遮挡,光电传感器会输出高电压,两光电传感器采集数据后与计算机相连.滑块在细线的牵引下向左加速运动,遮光条经过光电传感器A、B时,通过计算机可以得到如图乙所示的电压U随时间t变化的图线. 某粒子质量为m=1×10-18kg,电荷量为q=-1×10-8C,以v0=2$\sqrt{3}$×106m/s的速度与x轴成θ=$\frac{π}{3}$的角度射入磁感应强度为B=0.01T的匀强磁场中,最后落在x轴上的P点,如图所示(不计重力的作用).
某粒子质量为m=1×10-18kg,电荷量为q=-1×10-8C,以v0=2$\sqrt{3}$×106m/s的速度与x轴成θ=$\frac{π}{3}$的角度射入磁感应强度为B=0.01T的匀强磁场中,最后落在x轴上的P点,如图所示(不计重力的作用).