题目内容
1. 某粒子质量为m=1×10-18kg,电荷量为q=-1×10-8C,以v0=2$\sqrt{3}$×106m/s的速度与x轴成θ=$\frac{π}{3}$的角度射入磁感应强度为B=0.01T的匀强磁场中,最后落在x轴上的P点,如图所示(不计重力的作用).
某粒子质量为m=1×10-18kg,电荷量为q=-1×10-8C,以v0=2$\sqrt{3}$×106m/s的速度与x轴成θ=$\frac{π}{3}$的角度射入磁感应强度为B=0.01T的匀强磁场中,最后落在x轴上的P点,如图所示(不计重力的作用).求:(1)$\overline{OP}$的长度;
(2)粒子从由O点射入到落在P点所需的时间t.
分析 (1)粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律可以求出粒子的轨道半径,然后由几何知识求出OP间的距离.
(2)由几何知识求出粒子在磁场中转过的圆心角,然后求出粒子在磁场中的运动时间.
解答  解:(1)过O点和P点作速度方向的垂线,两线交点C即为粒子在磁场中做匀速圆周运动的圆心,如图所示,
解:(1)过O点和P点作速度方向的垂线,两线交点C即为粒子在磁场中做匀速圆周运动的圆心,如图所示,
则可知$\overline{OP}$=2R•sinθ
根据牛顿第二定律得
Bqv0=m$\frac{{v}_{0}^{2}}{R}$
解得:$\overline{OP}$=$\frac{2m{v}_{0}}{qB}$sinθ=6cm
(2)由图中可知:2θ=ωt=$\frac{2π}{T}$t
又v0=ωR=$\frac{2πR}{T}$
解得:t=$\frac{2θm}{qB}$=$\frac{2π}{3}×1{0}^{-8}$s
答:
(1)$\overline{OP}$的长度是6cm;
(2)粒子从由O点射入到落在P点所需的时间t是$\frac{2π}{3}×1{0}^{-8}$s.
点评 本题考查了求弦长、电子在磁场中的运动时间,知道电子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,应用牛顿第二定律及几何知识即可正确解题,作出电子的运动轨迹、求出电子转过的圆心角是正确解题的关键.

练习册系列答案
相关题目
11.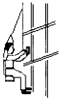 如图所示,清洗楼房玻璃的工人常用一根绳索将自己悬在空中,工作及其装备的总重量为G,绳索与竖直墙壁的夹角为α,绳索对工人的拉力大小为F1,墙壁对工人的弹力大小为F2,假定工人上升时姿式保持不变,不计一切摩擦及绳索的重力,则( )
如图所示,清洗楼房玻璃的工人常用一根绳索将自己悬在空中,工作及其装备的总重量为G,绳索与竖直墙壁的夹角为α,绳索对工人的拉力大小为F1,墙壁对工人的弹力大小为F2,假定工人上升时姿式保持不变,不计一切摩擦及绳索的重力,则( )
 如图所示,清洗楼房玻璃的工人常用一根绳索将自己悬在空中,工作及其装备的总重量为G,绳索与竖直墙壁的夹角为α,绳索对工人的拉力大小为F1,墙壁对工人的弹力大小为F2,假定工人上升时姿式保持不变,不计一切摩擦及绳索的重力,则( )
如图所示,清洗楼房玻璃的工人常用一根绳索将自己悬在空中,工作及其装备的总重量为G,绳索与竖直墙壁的夹角为α,绳索对工人的拉力大小为F1,墙壁对工人的弹力大小为F2,假定工人上升时姿式保持不变,不计一切摩擦及绳索的重力,则( )| A. | F1=$\frac{G}{sinα}$ | |
| B. | F2=$\frac{G}{sinα}$ | |
| C. | 若缓慢减小绳索的长度,F1与F2的合力变大 | |
| D. | 若缓慢减小绳索的长度,F1与F2都增大 |
12. 如图所示,间距为d的平行、光滑金属导轨,垂直放置在磁感应强度大小为B的匀强磁场中.质量为m的导体棒ab垂直于导轨放置,且与两导轨保持良好接触,现导体棒以初速度v0进入磁场,运动一段距离后速度为零.则此过程( )
如图所示,间距为d的平行、光滑金属导轨,垂直放置在磁感应强度大小为B的匀强磁场中.质量为m的导体棒ab垂直于导轨放置,且与两导轨保持良好接触,现导体棒以初速度v0进入磁场,运动一段距离后速度为零.则此过程( )
 如图所示,间距为d的平行、光滑金属导轨,垂直放置在磁感应强度大小为B的匀强磁场中.质量为m的导体棒ab垂直于导轨放置,且与两导轨保持良好接触,现导体棒以初速度v0进入磁场,运动一段距离后速度为零.则此过程( )
如图所示,间距为d的平行、光滑金属导轨,垂直放置在磁感应强度大小为B的匀强磁场中.质量为m的导体棒ab垂直于导轨放置,且与两导轨保持良好接触,现导体棒以初速度v0进入磁场,运动一段距离后速度为零.则此过程( )| A. | 导体棒做匀减速运动 | |
| B. | 导体棒上感应电流方向由a向b | |
| C. | 导体棒刚进入磁场时感应电动势大小为Bdv0 | |
| D. | 运动过程中回路中产生的焦耳热为$\frac{1}{2}$mv02 |
9.高一某同学在校运会上参加跳高比赛,其起跳后身体横着越过横杆,则其由起跳到最高点的过程中,克服重力做的功最接近( )
| A. | 5J | B. | 50J | C. | 500J | D. | 5000J |
13. 如图所示,一小物块以大小为v0的初速度从曲面的P点下滑,运动到Q点时速度大小仍为
如图所示,一小物块以大小为v0的初速度从曲面的P点下滑,运动到Q点时速度大小仍为
v0,若小物块以大小为v(v>v0)的初速度仍由P点下滑,则小物块运动到Q点时的速度大小为( )
 如图所示,一小物块以大小为v0的初速度从曲面的P点下滑,运动到Q点时速度大小仍为
如图所示,一小物块以大小为v0的初速度从曲面的P点下滑,运动到Q点时速度大小仍为v0,若小物块以大小为v(v>v0)的初速度仍由P点下滑,则小物块运动到Q点时的速度大小为( )
| A. | 大于v | B. | 等于v | ||
| C. | 小于v | D. | 条件不足,无法判断 |
10.大型强子对撞机加速一批质子,该对撞机“开足马力”后,能把数以百万计的粒子加速至接近3.0×108m/s,相当于光速的99.9%,粒子流每秒可在隧道内狂飙11245圈,单束粒子能量可达7万亿电子伏特.下列说法正确的是( )
| A. | 如果继续对粒子进行加速,粒子的速度将能够达到光速 | |
| B. | 如果继续对粒子进行加速,粒子的速度不能够超过光速 | |
| C. | 粒子高速运动时的质量将大于静止时的质量 | |
| D. | 粒子高速运动时的质量将小于静止时的质量 |
 如图,细绳的一端固定于O点,另一端系一个质量为m的小球,现在O点正下方的A点钉一个钉子,使细绳偏离竖直方向90°(细绳处于伸直状态),由静止释放小球.当细绳与钉子相碰时,小球对细绳的拉力为6mg.如将A点的钉子移至O点正下方的另一B点,小球仍从原来位置静止释放,细绳与钉子相碰,小球对细绳的拉力为4mg,已知A点与B点间距离h=0.2m,求细绳的长度l(不计一切摩擦和空气阻力,忽略小球大小).
如图,细绳的一端固定于O点,另一端系一个质量为m的小球,现在O点正下方的A点钉一个钉子,使细绳偏离竖直方向90°(细绳处于伸直状态),由静止释放小球.当细绳与钉子相碰时,小球对细绳的拉力为6mg.如将A点的钉子移至O点正下方的另一B点,小球仍从原来位置静止释放,细绳与钉子相碰,小球对细绳的拉力为4mg,已知A点与B点间距离h=0.2m,求细绳的长度l(不计一切摩擦和空气阻力,忽略小球大小). 如图所示,质量分别为M和m的物体A和B静止在光滑水平面上,A左侧被很簿的油泥层粘在竖直墙壁上,AB之间用一轻质弹簧相连,现用一水平向右的外力F作用在B上,外力作用一段时间后,A离开墙壁开始运动,此时撤掉外力,且弹簧此时的弹性势能为E1,在以后的运动过程中,弹簧弹性势能的最大值为E2,设外力F对B的冲量为I0,求从静止到A开始运动的过程中A受到油泥层黏力的冲量I的大小.
如图所示,质量分别为M和m的物体A和B静止在光滑水平面上,A左侧被很簿的油泥层粘在竖直墙壁上,AB之间用一轻质弹簧相连,现用一水平向右的外力F作用在B上,外力作用一段时间后,A离开墙壁开始运动,此时撤掉外力,且弹簧此时的弹性势能为E1,在以后的运动过程中,弹簧弹性势能的最大值为E2,设外力F对B的冲量为I0,求从静止到A开始运动的过程中A受到油泥层黏力的冲量I的大小. 在《探究力的平行四边形定则》实验中,某同学的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图,则:
在《探究力的平行四边形定则》实验中,某同学的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图,则: