题目内容
5. 如图所示,质量m=1kg的小球用细线拴住,线长l=0.5m,细线所受拉力达到F=18N时就会被拉断.当小球从图示位置释放后摆到悬点的正下方时,细线恰好被拉断.若此时小球距水平地面的高度h=5m.试求:
如图所示,质量m=1kg的小球用细线拴住,线长l=0.5m,细线所受拉力达到F=18N时就会被拉断.当小球从图示位置释放后摆到悬点的正下方时,细线恰好被拉断.若此时小球距水平地面的高度h=5m.试求:(1)绳子刚断时,小球的速度大小是多少,
(2)从绳子断开到小球落地时经历了多长时间,
(3)小球落地时速度.
分析 (1)在最低点,根据最大拉力,结合牛顿第二定律求出小球的速度大小.
(2)根据高度,结合位移时间公式求出小球平抛运动的时间.
(3)根据速度时间公式求出落地时竖直分速度,结合平行四边形定则求出落地速度的大小和方向.
解答 解:(1)在最低点,根据牛顿第二定律得:F-mg=$m\frac{{v}^{2}}{R}$,
代入数据解得:v=2m/s.
(2)绳子断开后,小球做以初速度为v0=2m/s的平抛运动,根据h=$\frac{1}{2}g{t}^{2}$得:t=$\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×5}{10}}s=1s$.
(3)小球落地时的竖直分速度为:vy=gt=10×1m/s=10m/s,
根据平行四边形定则知,小球落地的速度为:v=$\sqrt{{{v}_{0}}^{2}+{{v}_{y}}^{2}}=\sqrt{4+100}$m/s≈10.2m/s,
设落地时速度方向与水平方向成θ角度,则有:tanθ=$\frac{{v}_{y}}{{v}_{0}}=\frac{10}{2}=5$.
答:(1)绳子刚断时,小球的速度大小是2m/s;
(2)从绳子断开到小球落地时经历了1s时间;
(3)小球落地时的速度大小为10.2m/s,速度方向与水平方向的夹角正切值为5.
点评 本题考查了圆周运动和平抛运动的综合运用,知道圆周运动向心力的来源,以及平抛运动在水平方向和竖直方向上的运动规律是解决本题的关键.

练习册系列答案
相关题目
15. 如图所示,半径为r的转盘固定在水平桌面上,可绕过圆心O的竖直轴转动;一根长为l的轻绳的一端系质量为m的小球,另一端固定在转盘的边缘上,绳子绷直时与桌面平行.当转盘以角速度ω匀速转动时,绳子不会缠绕在转盘上,小球在桌面上做匀速圆周运动,在运动过程中绳子与转盘的边缘相切,不计空气阻力,下列判断正确的是( )
如图所示,半径为r的转盘固定在水平桌面上,可绕过圆心O的竖直轴转动;一根长为l的轻绳的一端系质量为m的小球,另一端固定在转盘的边缘上,绳子绷直时与桌面平行.当转盘以角速度ω匀速转动时,绳子不会缠绕在转盘上,小球在桌面上做匀速圆周运动,在运动过程中绳子与转盘的边缘相切,不计空气阻力,下列判断正确的是( )
 如图所示,半径为r的转盘固定在水平桌面上,可绕过圆心O的竖直轴转动;一根长为l的轻绳的一端系质量为m的小球,另一端固定在转盘的边缘上,绳子绷直时与桌面平行.当转盘以角速度ω匀速转动时,绳子不会缠绕在转盘上,小球在桌面上做匀速圆周运动,在运动过程中绳子与转盘的边缘相切,不计空气阻力,下列判断正确的是( )
如图所示,半径为r的转盘固定在水平桌面上,可绕过圆心O的竖直轴转动;一根长为l的轻绳的一端系质量为m的小球,另一端固定在转盘的边缘上,绳子绷直时与桌面平行.当转盘以角速度ω匀速转动时,绳子不会缠绕在转盘上,小球在桌面上做匀速圆周运动,在运动过程中绳子与转盘的边缘相切,不计空气阻力,下列判断正确的是( )| A. | 小球做圆周运动的线速度的大小v=ωl | |
| B. | 小球做圆周运动的线速度的大小v=ω$\sqrt{{r}^{2}+{l}^{2}}$ | |
| C. | 绳对小球的拉力大小为FT=mω2$\sqrt{{l}^{2}+{r}^{2}}$ | |
| D. | 绳对小球的拉力大小为FT=$\frac{m{ω}^{2}({l}^{2}+{r}^{2})}{l}$ |
16.下列关于动量的说法正确的是( )
| A. | 质量大的物体动量大 | B. | 速度大的物体动量大 | ||
| C. | 动量的方向与速度的方向相同 | D. | 动量的方向可能与速度方向相反 |
17.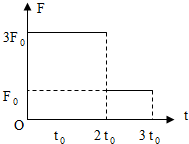 质量为m的物体静止在光滑水平面上,从t=0时刻开始受到水平力的作用.力的大小F与时间t的关系如图所示,力的方向保持不变,则( )
质量为m的物体静止在光滑水平面上,从t=0时刻开始受到水平力的作用.力的大小F与时间t的关系如图所示,力的方向保持不变,则( )
 质量为m的物体静止在光滑水平面上,从t=0时刻开始受到水平力的作用.力的大小F与时间t的关系如图所示,力的方向保持不变,则( )
质量为m的物体静止在光滑水平面上,从t=0时刻开始受到水平力的作用.力的大小F与时间t的关系如图所示,力的方向保持不变,则( )| A. | 3t0时刻的瞬时功率为$\frac{{5F_0^2{t_0}}}{m}$ | |
| B. | 3t0时刻的瞬时功率为$\frac{{7F_0^2{t_0}}}{m}$ | |
| C. | 在t=0到3t0这段时间内,水平力的平均功率为$\frac{{49F_0^2{t_0}}}{6m}$ | |
| D. | 在t=0到3t0这段时间内,水平力的平均功率为$\frac{{25F_0^2{t_0}}}{6m}$ |
14.下列关于分子热运动的说法中正确的是( )
| A. | 布朗运动就是液体分子的热运动 | |
| B. | 气体如果失去了容器的约束就会散开,这是因为气体分子之间存在斥力 | |
| C. | 对于一定量的理想气体,如果压强不变,体积增大,那么它的内能一定减小 | |
| D. | 如果气体温度升高,分子平均动能会增加,但并不是所有分子的速率都增大 |
9.一个质量为m的物体以a=2g的加速度竖直向上做匀加速运动,则在物体上升h高度的过程中,物体的( )
| A. | 重力势能增加了2mgh | B. | 重力势能增加了mgh | ||
| C. | 动能增加了2mgh | D. | 动能增加了mgh |

 如图所示的部分纸带记录了“测定匀变速直线运动的加速度”实验小车匀加速运动的情况,已知按打点先后记录的各计数点A、B、C、D之间的时间间隔相同,AB=13.0cm,BC=19.0cm,CD=25.0cm,打B点时小车运动的速度大小为0.8m/s,则A与B之间的时间间隔为△T=0.2S,小车运动的加速度大小是1.5m/s2,方向向左(填左或右).
如图所示的部分纸带记录了“测定匀变速直线运动的加速度”实验小车匀加速运动的情况,已知按打点先后记录的各计数点A、B、C、D之间的时间间隔相同,AB=13.0cm,BC=19.0cm,CD=25.0cm,打B点时小车运动的速度大小为0.8m/s,则A与B之间的时间间隔为△T=0.2S,小车运动的加速度大小是1.5m/s2,方向向左(填左或右).