题目内容
11. 一质量m=2kg的质点在空中以速度vo=2m/s沿y轴正方向(竖直方向)运动,经过原点O后始终受到一个沿X轴正方向(水平方向)的恒力F=20N作用,不计空气阻力,g=10m/s2求:
一质量m=2kg的质点在空中以速度vo=2m/s沿y轴正方向(竖直方向)运动,经过原点O后始终受到一个沿X轴正方向(水平方向)的恒力F=20N作用,不计空气阻力,g=10m/s2求:(1)质点在最高点M的坐标;
(2)质点再次回到X轴时与X轴交点为N,大致画出质点从O点到N点轨迹并求出N点的坐标;
(3)求质点经过N点的速度大小.
分析 (1)将运动分解成x与y轴方向,结合分运动与合运动等时性,及运动学公式,即可求解;
(2)根据抛体运动的特征,结合x方向匀加速直线运动,而y方向竖直上抛运动,从而即可求解;
(3)根据矢量的合成法则,结合速度公式,即可求解.
解答 解:(1)将运动分解成x方向匀加速直线运动,而y方向竖直上抛运动,
质点在空中以速度vo=2m/s沿y轴正方向(竖直方向)运动,
则运动时间t=$\frac{{v}_{0}}{g}$=$\frac{2}{10}$=0.2s;竖直方向的位移h=${v}_{o}t-\frac{1}{2}g{t}^{2}$=2×0.2-$\frac{1}{2}×10×0.{2}^{2}$=0.2m;
而受到一个沿X轴正方向(水平方向)的恒力F=20N作用,
那么水平方向的位移x=$\frac{1}{2}a{t}^{2}$=$\frac{1}{2}×\frac{20}{2}×0.{2}^{2}$=0.2m
因此质点在最高点M的坐标(0.2m,0.2m);
(2)在y轴方向先向上匀减速直线运动,再向下匀加速直线运动,时间相等,
在水平方向做匀加速直线运动,根据曲线运动条件,及抛体运动的特征,
运动轨迹,如图所示:
由上可知,质点从O点到N点的时间为t″=0.4s;
那么对应的位移为x′=$\frac{1}{2}at{″}^{2}$=$\frac{1}{2}×10×0.{4}^{2}$=0.8m;
因此N点的坐标(0,0.8m);
(3)根据速度公式,那么x方向的速度大小,vx=at″=10×0.4=4m/s;
而y方向的速度大小为,vx=2m/s;
依据速度的合成法则,则质点经过N点的速度大小vN=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$m/s
答:(1)质点在最高点M的坐标(0.2m,0.2m);
(2)质点从O点到N点轨迹如上图所示,N点的坐标(0,0.8m);
(3)质点经过N点的速度大小2$\sqrt{5}$m/s.
点评 考查运动的合成与分解的应用,掌握矢量的合成法则,理解运动学公式的内容,注意分运动与合运动的等时性,并理解抛体运动的特征.

| A. | 研究地球绕太阳做圆周运动中的地球 | |
| B. | 研究地球自转时的地球 | |
| C. | 研究花样滑冰姿态时的运动员 | |
| D. | 研究花样滑冰运动员的运动路线时的运动员 |
| A. | 不可能从单一热源吸收能量,使之完全变成功,而不产生其他影响 | |
| B. | 农民锄松土壤,是为了破坏土壤里的毛细管,保存土壤里的水分 | |
| C. | 随着分子间距增大,分子间的引力和斥力都减小,但斥力减小更快,合力表现为引力 | |
| D. | 温度升高,每个分子热运动的动能越大 | |
| E. | 对某种气体而言,已知阿伏伽德罗常数、气体的摩尔质量和密度,可计算出该种气体分子间的平均距离 |
| A. | 甲、乙两球的距离越来越大 | B. | 甲、乙两球的距离始终保持不变 | ||
| C. | 甲、乙两球的速度之差越来越大 | D. | 甲、乙两球的速度之差保持不变 |
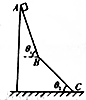 如图所示,AB与BC是两个场地相同的斜面,但倾角不同,AB与水平方向夹角为θ1,BC与水平方向夹角为θ2,两斜面间用光滑的小圆弧连接,物体通过时无能量损失,一物块从A点由静止释放,运动到C点速度刚好为0.已知物块与两斜面的动摩擦因数相同,则物块与两斜面的动摩擦因数为( )
如图所示,AB与BC是两个场地相同的斜面,但倾角不同,AB与水平方向夹角为θ1,BC与水平方向夹角为θ2,两斜面间用光滑的小圆弧连接,物体通过时无能量损失,一物块从A点由静止释放,运动到C点速度刚好为0.已知物块与两斜面的动摩擦因数相同,则物块与两斜面的动摩擦因数为( )| A. | $\frac{2}{cos{θ}_{1}+cot{θ}_{2}}$ | B. | $\frac{cos{θ}_{1}+cos{θ}_{2}}{sin{θ}_{1}+sin{θ}_{2}}$ | ||
| C. | $\frac{sin{θ}_{1}-sin{θ}_{2}}{cos{θ}_{1}-cos{θ}_{2}}$ | D. | $\frac{sin{θ}_{1}+sin{θ}_{2}}{cos{θ}_{1}+cos{θ}_{2}}$ |

 在一长为2L的轻杆的一端和中间分别固定质量相同的小球,杆的另一端可绕一无摩擦的轴转动.现将杆由竖直位置无初速度释放,则杆运动到水平位置时,两球的速度各为多大?
在一长为2L的轻杆的一端和中间分别固定质量相同的小球,杆的另一端可绕一无摩擦的轴转动.现将杆由竖直位置无初速度释放,则杆运动到水平位置时,两球的速度各为多大?