题目内容
1．
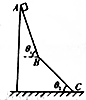如图所示，AB与BC是两个场地相同的斜面，但倾角不同，AB与水平方向夹角为θ1，BC与水平方向夹角为θ2，两斜面间用光滑的小圆弧连接，物体通过时无能量损失，一物块从A点由静止释放，运动到C点速度刚好为0．已知物块与两斜面的动摩擦因数相同，则物块与两斜面的动摩擦因数为（ ）| A． | $\frac{2}{cos{θ}_{1}+cot{θ}_{2}}$ | B． | $\frac{cos{θ}_{1}+cos{θ}_{2}}{sin{θ}_{1}+sin{θ}_{2}}$ | ||
| C． | $\frac{sin{θ}_{1}-sin{θ}_{2}}{cos{θ}_{1}-cos{θ}_{2}}$ | D． | $\frac{sin{θ}_{1}+sin{θ}_{2}}{cos{θ}_{1}+cos{θ}_{2}}$ |
分析 对全过程运用动能定理列式可求得动摩擦因数．整个过程中，物块动能的变化量为零，重力做正功，摩擦力做负功．由动能定理求解．
解答 解：对全过程，由动能定理得：
mgsinθ1•$\overline{AB}$-μmgcosθ1•$\overline{AB}$+mgsinθ2•$\overline{BC}$-μmgcosθ2•$\overline{BC}$=0
据题，$\overline{AB}$=$\overline{BC}$
联立解得 μ=$\frac{sin{θ}_{1}+sin{θ}_{2}}{cos{θ}_{1}+cos{θ}_{2}}$，故ABC错误，D正确．
故选：D
点评 在运用动能定理解题时首先要确定研究的过程，分析有哪些力做功，最后根据动能定理列出表达式进行求解．本题也可以分两段分别列式解答．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
一质量m=2kg的质点在空中以速度vo=2m/s沿y轴正方向（竖直方向）运动，经过原点O后始终受到一个沿X轴正方向（水平方向）的恒力F=20N作用，不计空气阻力，g=10m/s2求：
9．
2014年12月31日，搭载“风云二号”08星的运载火箭在西昌卫星发射中心点火发射．发射过程中“风云二号”08星的某一运行轨道为椭圆轨道，周期为T0，如图所示．则（ ）
2014年12月31日，搭载“风云二号”08星的运载火箭在西昌卫星发射中心点火发射．发射过程中“风云二号”08星的某一运行轨道为椭圆轨道，周期为T0，如图所示．则（ ）| A． | “风云二号”08星的发射速度小于第一宇宙速度 | |
| B． | “风云二号”08星在A→B→C的过程中，速率逐渐减小 | |
| C． | “风云二号”08星在A→B过程所用的时间小于$\frac{{T}_{0}}{4}$ | |
| D． | “风云二号”08星在B→C→D的过程中，万有引力对它先做正功后做负功 |
16．一同学要研究轻质弹簧的弹性势能与弹簧长度改变量的关系．实验装置如下图甲所示，在离地面高为h的光滑水平桌面上，沿着与桌子右边缘垂直的方向放置一轻质弹簧，其左端固定，右端与质量为m的小刚球接触．将小球向左压缩弹簧一段距离后由静止释放，使小球沿水平方向射出桌面，小球在空中飞行落到位于水平地面的记录纸上留下痕迹．重力加速度为g．
（1）若测得某次压缩弹簧释放后小球落点P痕迹到O点的距离为s，则释放小球前弹簧的弹性势能表达式为$\frac{mg{s}^{2}}{4h}$；（用m、g、s、h等四个字母表示）
（2）该同学改变弹簧的压缩量进行多次测量得到下表一组数据：
根据表中已有数据，表中缺失的数据可能是s=60.00cm；
（3）完成实验后，该同学对上述装置进行了如图乙所示的改变：
（I）在木板表面先后钉上白纸和复写纸，并将木板竖直立于靠近桌子右边缘处，使小球向左压缩弹簧一段距离后由静止释放，撞到木板并在白纸上留下痕迹O；（II）将木板向右平移适当的距离固定，再使小球向左压缩弹簧一段距离后由静止释放，撞到木板上得到痕迹P；（III）用刻度尺测量纸上O点到P点的竖直距离为y．若已知木板与桌子右边缘的水平距离为L，则（II）步骤中弹簧的压缩量应该为$\frac{L}{20}\sqrt{\frac{h}{y}}$．（用L、h、y等三个字母表示）
（1）若测得某次压缩弹簧释放后小球落点P痕迹到O点的距离为s，则释放小球前弹簧的弹性势能表达式为$\frac{mg{s}^{2}}{4h}$；（用m、g、s、h等四个字母表示）
（2）该同学改变弹簧的压缩量进行多次测量得到下表一组数据：
| 弹簧压缩量x/cm | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 |
| 小球飞行水平距离s/cm | 20.10 | 30.00 | 40.10 | 49.90 | 69.90 |
（3）完成实验后，该同学对上述装置进行了如图乙所示的改变：
（I）在木板表面先后钉上白纸和复写纸，并将木板竖直立于靠近桌子右边缘处，使小球向左压缩弹簧一段距离后由静止释放，撞到木板并在白纸上留下痕迹O；（II）将木板向右平移适当的距离固定，再使小球向左压缩弹簧一段距离后由静止释放，撞到木板上得到痕迹P；（III）用刻度尺测量纸上O点到P点的竖直距离为y．若已知木板与桌子右边缘的水平距离为L，则（II）步骤中弹簧的压缩量应该为$\frac{L}{20}\sqrt{\frac{h}{y}}$．（用L、h、y等三个字母表示）
如图所示，在某一均匀介质中，A、B是振动情况完全相同的两个波源，其振动方程均为y=0.2sin20πt（m），介质中P点与A、B两波源间的距离分别为7.5m和10m，两波源形成的简谐波沿各个方向传播，波速都为10m/s，则A、B两点连线上相邻的振动加强点间距为0.5m，P点的振动是减弱（填“加强”或“减弱”）的．
如图所示，一个固定在竖直平面上的光滑半圆形管道，管道里有一个直径略小于管道内径的小球，小球在管道内做圆周运动，从B点脱离后做平抛运动，经过0.3秒后又恰好垂直与倾角为45°的斜面相碰到．已知圆轨道半径为R=1m，小球的质量为m=1kg，g取10m/s2．求
10．下列说法正确的是（ ）
| A． | 固体分子间无间隙，液体分子间稍有空隙，气体分子间距约为10r0 | |
| B． | 液体与固体接触处的附着层内分子间距比液体分子间距大，与气体接触表面层内液体分子间距比液体内分子间距小 | |
| C． | 分子合力图象有三个单调区，物质呈固态说明分子间既有引力也有斥力 | |
| D． | 布朗运动是由周围液体大量分子对颗粒的频繁的无规则碰撞引起的 | |
| E． | 扩散现象说明分子间有空隙 |
