题目内容
19．
用控制变量法，可以研究影响平行板电容器电容C的因素．设两极板正对面积为S，极板间的距离为d．极板所带电荷量为Q，静电计指针偏角为θ．实验中（ ）| A． | 保持Q、S不变，增大d，则θ变大，C变小 | |
| B． | 保持d、S不变．增大Q．则θ变大，C变大 | |
| C． | 保持Q、d不变，减小S．则θ变小，C变小 | |
| D． | 保持Q、S、d不变，在两极板间插入电介质．则θ变小，C变小 |
分析 静电计测定电容器极板间的电势差，电势差越大，指针的偏角越大．根据电容的决定式C=$\frac{?S}{4πkd}$分析极板间距离、正对面积变化时电容的变化情况，由于极板所带电荷量不变，再由电容的定义式C=$\frac{Q}{U}$ 分析板间电势差的变化，即可再确定静电计指针的偏角变化情况．
解答 解：A、B、根据电容的决定式C=$\frac{?S}{4πkd}$得知，电容与极板间距离成反比，当保持Q、S不变，增大d时，电容C减小，因电容器的电量Q不变，由电容的定义式C=$\frac{Q}{U}$ 分析可知板间电势差增大，则静电计指针的偏角θ变大．故A正确；
B、当保持d、S不变，增大Q时，根据电容的决定式C=$\frac{?S}{4πkd}$得知，电容C不变，由电容的定义式C=$\frac{Q}{U}$ 分析可知板间电势差增大，则θ变大，B错误．
C、根据电容的决定式C=$\frac{?S}{4πkd}$得知，电容与极板的正对面积成正比，当保持d不变，减小S时，电容C减小，电容器极板所带的电荷量Q不变，则由电容的定义式C=$\frac{Q}{U}$ 分析可知板间电势差增大，静电计指针的偏角θ变大，故C错误；
D、当保持Q、S、d不变，在两极板间插入电介质，根据电容的决定式C=$\frac{?S}{4πkd}$得知，电容C变大，而由电容的定义式C=$\frac{Q}{U}$ 分析可知板间电势差减小，则θ变小，故D错误．
故选：A．
点评 本题是电容动态变化分析问题，关键抓住两点：一是电容器的电量不变；二是掌握电容的两个公式：电容的决定式C=$\frac{?S}{4πkd}$和C=$\frac{Q}{U}$．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，一水平放置的平行板电容器的两极板间距为d，极板间电压为U0，A板带正电，B板带负电，电容器上方有一个宽度为d足够长的匀强磁场，磁场方向垂直纸面向里，一个质量为m、电荷量为q的带正电微粒（不计重力）从A板边缘以水平向左的速度v0进人电容器，由于存在某种外力使粒子在水平方向做匀减速运动，经过一段时间后粒子从B上一个小孔N进人磁场，进人磁场的速度方向与竖直向上方向的夹角为37°．小孔N距离B板右端的距离也为d（sin37°=0.6）．试求：
10．下列说法中，不符合物理学史实的是（ ）
| A． | 牛顿总结出了万物间相互作用的规律 | |
| B． | 亚里士多德认为，力是物体运动状态改变的原因，而不是物体运动的原因 | |
| C． | 密立根测得电荷量e的数值 | |
| D． | 奥斯特发现导线通电时，导线附近的小磁针发生偏转 |
7．
一倾角为θ=37°的粗糙斜面与一光滑的半径R=0.9m的竖直圆轨道相切于P点，O点是轨道圆心，轨道上的B点是最高点，D点是最低点，C点是最右的点，斜面上的A点与B点等高．一质量m=1.0kg的小物块在A点以沿斜面向下的初速度v0刚好能在斜面上匀速运动，通过P点处的小孔进入圆轨道并恰能做完整的圆周运动．g=10m/s2，sin37°=0.6，cos37°=0.8．则下列说法正确的是（ ）
一倾角为θ=37°的粗糙斜面与一光滑的半径R=0.9m的竖直圆轨道相切于P点，O点是轨道圆心，轨道上的B点是最高点，D点是最低点，C点是最右的点，斜面上的A点与B点等高．一质量m=1.0kg的小物块在A点以沿斜面向下的初速度v0刚好能在斜面上匀速运动，通过P点处的小孔进入圆轨道并恰能做完整的圆周运动．g=10m/s2，sin37°=0.6，cos37°=0.8．则下列说法正确的是（ ）| A． | v0=3m/s | |
| B． | 小物块与斜面间的动摩擦因数μ=0.6 | |
| C． | 小物块在D点时对轨道压力F0=60N | |
| D． | 小物块在C点受到的合外力水平向左 |
4．丹麦物理学家奥斯特在1820年通过实验发现电流磁效应现象，下列说法正确的是（ ）
| A． | 奥斯特在实验中观察到电流磁效应，揭示了电磁感应定律 | |
| B． | 将直导线沿东西方向水平放置，把小磁针放在导线的正下方，给导线通以足够大电流，小磁针一定会转动 | |
| C． | 将直导线沿南北方向水平放置，把小磁针放在导线的正下方，给导线通以足够大电流，小磁针一定会转动 | |
| D． | 将直导线沿南北方向水平放置，把铜针（用铜制成的指针）放在导线的正下方，给导线通以足够大电流，铜针一定会转动 |
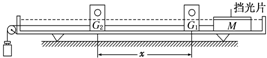
8．
伽利略在研究自由落体运动时，做了如下实验．他让一个铜球从阻力很小（可忽略不计）的斜面上由静止开始滚下，并且重复做了上百次实验．假设某次实验中伽利略是这样做的：在斜面上任取三个位置A、B、C，如图所示．让小球分别由A、B、C位置从静止滚下，A、B、C与斜面底端的距离分别为xl、x2、x3．小球由A、B、C运动到斜面底端的时间分别为t1、t2、t3，速度分别为vl、v2、v3，则下列关系式中正确并且是伽利略用来证明小球沿光滑斜面向下运动是匀变速直线运动的是（ ）
伽利略在研究自由落体运动时，做了如下实验．他让一个铜球从阻力很小（可忽略不计）的斜面上由静止开始滚下，并且重复做了上百次实验．假设某次实验中伽利略是这样做的：在斜面上任取三个位置A、B、C，如图所示．让小球分别由A、B、C位置从静止滚下，A、B、C与斜面底端的距离分别为xl、x2、x3．小球由A、B、C运动到斜面底端的时间分别为t1、t2、t3，速度分别为vl、v2、v3，则下列关系式中正确并且是伽利略用来证明小球沿光滑斜面向下运动是匀变速直线运动的是（ ）| A． | $\frac{{v}_{1}}{{t}_{1}}$=$\frac{{v}_{2}}{{t}_{2}}$=$\frac{{v}_{3}}{{t}_{3}}$ | B． | $\frac{{v}_{1}}{2}$=$\frac{{v}_{2}}{2}$=$\frac{{v}_{3}}{2}$ | ||
| C． | $\frac{{x}_{1}}{{t}_{1}^{2}}$=$\frac{{x}_{2}}{{t}_{2}^{2}}$=$\frac{{x}_{3}}{{t}_{3}^{2}}$ | D． | x1-x2=x2-x3 |