题目内容
11.为了探究加速度与力的关系,使用如图所示的气垫导轨装置进行实验.其中G1、G2为两个光电门,当滑块通过G1、G2光电门时,光束被遮挡的时间t1、t2都可以被测量并记录,滑块连同上面固定的条形挡光片的总质量为M,挡光片宽度为D,光电门间距离为x,牵引砝码的质量为m. 实验开始应先调节气垫导轨下面的螺钉,使气垫导轨水平.回答下列问题: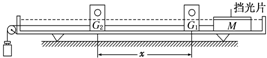
(1)若取细绳牵引滑块的拉力T=mg,测得滑块质量M=0.2kg,改变m的值,进行多次实验,以下m的取值不合适的一个是D.
A.m1=5g B.m2=15g C.m3=20g D.m4=200g
(2)在此实验中,需要测得每一个牵引力对应的加速度,其中求得的加速度的表达式为
a=$\frac{{{{(\frac{D}{t_2})}^2}-{{(\frac{D}{t_1})}^2}}}{2x}$(用t1、t2、D、x表示).
(3)以小车和牵引砝码为研究对象,小车质量M一定,改变牵引砝码的质量m,根据实验数据描绘的小车加速度a与牵引砝码的质量m之间的实验关系图象.能正确反映$\frac{1}{a}$-$\frac{1}{m}$关系的图是C.
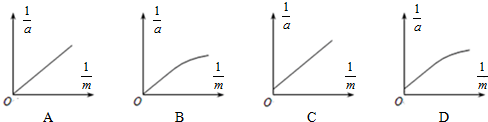
分析 (1)在实验中,认为m的重力等于滑块所受的合力,所以m的质量应远小于M的质量.
(2)根据v22-v12=2ax,结合v=$\frac{D}{t}$求出加速度的表达式.
(3)根据牛顿第二定律得出$\frac{1}{a}$-$\frac{1}{m}$的关系式,从而选择图象.
解答 解:(1)在实验中,认为m的重力等于滑块所受的合力,所以m的质量应远小于M的质量.故D不合适.
本题选不合适的,故选:D.
(2)滑块经过光电门的速度为:v2=$\frac{D}{{t}_{2}}$,v1=$\frac{D}{{t}_{1}}$,
则根据据v22-v12=2ax,得:a=$\frac{(\frac{D}{{t}_{2}})^{2}-(\frac{D}{{t}_{1}})^{2}}{2x}$.
(3)根据牛顿第二定律,则有:a=$\frac{mg}{M+m}$,$\frac{1}{a}$=$\frac{M}{g}$$\frac{1}{m}$+$\frac{1}{g}$,
则:$\frac{1}{a}$-$\frac{1}{m}$图象是一条倾斜的直线,且在纵轴上有截距,故C正确.故选:C;
故答案为:(1)D;(2)$\frac{{{{(\frac{D}{t_2})}^2}-{{(\frac{D}{t_1})}^2}}}{2x}$;(3)C.
点评 解决本题的关键理解实验的原理,知道当m的质量远小于M的质量,m的重力可以认为等于M所受的合力,计算加速度时利用运动学公式求解.以及推导出$\frac{1}{a}$与$\frac{1}{m}$关系式,进而选择图象,难度适中.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
2.用同一实验装置甲研究光电效应现象,分别用A、B、C三束光照射光电管阴极,得到光管两端电压与相应的光电流的关系如图乙所示,其中A、C两束光照射时对应的遏止电压相同,均为Uc1,根据你所学的相关理论下列论述正确的是( )


| A. | 三个光束的频率都大于阴极金属板的极限频率 | |
| B. | B光束光子的动量最大 | |
| C. | 三个光束中B光束照射时单位时间内产生的光电子数量最多 | |
| D. | 三个光束中A光束照射时单位时间内产生的光电子数量最多 | |
| E. | 若B光是氢原子由第2能级向基态跃迁时产生的,则C光可能是氢原子由更高能级跃迁到基态产生的 |
19. 用控制变量法,可以研究影响平行板电容器电容C的因素.设两极板正对面积为S,极板间的距离为d.极板所带电荷量为Q,静电计指针偏角为θ.实验中( )
用控制变量法,可以研究影响平行板电容器电容C的因素.设两极板正对面积为S,极板间的距离为d.极板所带电荷量为Q,静电计指针偏角为θ.实验中( )
 用控制变量法,可以研究影响平行板电容器电容C的因素.设两极板正对面积为S,极板间的距离为d.极板所带电荷量为Q,静电计指针偏角为θ.实验中( )
用控制变量法,可以研究影响平行板电容器电容C的因素.设两极板正对面积为S,极板间的距离为d.极板所带电荷量为Q,静电计指针偏角为θ.实验中( )| A. | 保持Q、S不变,增大d,则θ变大,C变小 | |
| B. | 保持d、S不变.增大Q.则θ变大,C变大 | |
| C. | 保持Q、d不变,减小S.则θ变小,C变小 | |
| D. | 保持Q、S、d不变,在两极板间插入电介质.则θ变小,C变小 |
6.在电磁学发展过程中,许多科学家做出了贡献.下列说法正确的是( )
| A. | 法拉第发现了电磁感应现象 | |
| B. | 安培发现了电流磁效应 | |
| C. | 库仑提出了用电场线来形象描述电场 | |
| D. | 麦克斯韦预言了电磁波并且实验证实了电磁波的存在 |
16. 如图所示,竖直放置在水平面上的圆筒,从圆筒上边缘等高处同一位置分别紧贴内壁和外壁以相同速率向相反方向水平发射两个相同小球,直至小球落地,不计空气阻力和所有摩擦,以下说法正确的是( )
如图所示,竖直放置在水平面上的圆筒,从圆筒上边缘等高处同一位置分别紧贴内壁和外壁以相同速率向相反方向水平发射两个相同小球,直至小球落地,不计空气阻力和所有摩擦,以下说法正确的是( )
 如图所示,竖直放置在水平面上的圆筒,从圆筒上边缘等高处同一位置分别紧贴内壁和外壁以相同速率向相反方向水平发射两个相同小球,直至小球落地,不计空气阻力和所有摩擦,以下说法正确的是( )
如图所示,竖直放置在水平面上的圆筒,从圆筒上边缘等高处同一位置分别紧贴内壁和外壁以相同速率向相反方向水平发射两个相同小球,直至小球落地,不计空气阻力和所有摩擦,以下说法正确的是( )| A. | 筒外的小球先落地 | |
| B. | 两小球的落地速度可能相同 | |
| C. | 两小球通过的路程不一定相等 | |
| D. | 筒内小球随着速率的增大.对筒壁的压力逐渐增加 |
3.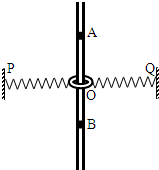 如图所示,一个质量为m的刚性圆环套在粗糙的竖直固定细杆上,圆环的直径略大于细杆的直径,圆环的两边与两个相同的轻质弹簧的一端相连,轻质弹簧的另一端连在和圆环同一高度的墙壁上的P、Q两点处,弹簧的劲度系数为k,起初圆环处于O点,弹簧处于原长状态且弹簧的原长为L,细杆上面的A、B两点到O点的距离都为L,将圆环拉至A点由静止释放,重力加速度为g,对于圆环从A点运动到B点的过程,下列说法正确的是( )
如图所示,一个质量为m的刚性圆环套在粗糙的竖直固定细杆上,圆环的直径略大于细杆的直径,圆环的两边与两个相同的轻质弹簧的一端相连,轻质弹簧的另一端连在和圆环同一高度的墙壁上的P、Q两点处,弹簧的劲度系数为k,起初圆环处于O点,弹簧处于原长状态且弹簧的原长为L,细杆上面的A、B两点到O点的距离都为L,将圆环拉至A点由静止释放,重力加速度为g,对于圆环从A点运动到B点的过程,下列说法正确的是( )
 如图所示,一个质量为m的刚性圆环套在粗糙的竖直固定细杆上,圆环的直径略大于细杆的直径,圆环的两边与两个相同的轻质弹簧的一端相连,轻质弹簧的另一端连在和圆环同一高度的墙壁上的P、Q两点处,弹簧的劲度系数为k,起初圆环处于O点,弹簧处于原长状态且弹簧的原长为L,细杆上面的A、B两点到O点的距离都为L,将圆环拉至A点由静止释放,重力加速度为g,对于圆环从A点运动到B点的过程,下列说法正确的是( )
如图所示,一个质量为m的刚性圆环套在粗糙的竖直固定细杆上,圆环的直径略大于细杆的直径,圆环的两边与两个相同的轻质弹簧的一端相连,轻质弹簧的另一端连在和圆环同一高度的墙壁上的P、Q两点处,弹簧的劲度系数为k,起初圆环处于O点,弹簧处于原长状态且弹簧的原长为L,细杆上面的A、B两点到O点的距离都为L,将圆环拉至A点由静止释放,重力加速度为g,对于圆环从A点运动到B点的过程,下列说法正确的是( )| A. | 圆环通过O点的加速度小于g | |
| B. | 圆环在O点的速度最大 | |
| C. | 圆环在A点时的加速度大小为g+$\frac{(2-\sqrt{2})kL}{m}$ | |
| D. | 圆环在B点的速度为2$\sqrt{gL}$ |

 如图所示为氢原子的能级图,n为量子数.若氢原子由n=3跃迁到n=2的过程释放出的光子恰好能使某种金属产生光电效应,则一群处于n=4的氢原子在向基态跃迁时,产生的光子中有4种频率的光子能使该金属产生光电效应,其中光电子的最大初动能Ekm=10.86eV.
如图所示为氢原子的能级图,n为量子数.若氢原子由n=3跃迁到n=2的过程释放出的光子恰好能使某种金属产生光电效应,则一群处于n=4的氢原子在向基态跃迁时,产生的光子中有4种频率的光子能使该金属产生光电效应,其中光电子的最大初动能Ekm=10.86eV. 风力发电作为新型环保新能源,近几年来得到了快速发展.如图是所建的风车阵.如果风车阵中发电机总输出功率为100kW,输出电压是250V,先后经过升压变压器和降压变压器传输到用户,设输电线的总电阻为10Ω.若要求输电线中因发热而损失的功率为输送功率的4%,试求:
风力发电作为新型环保新能源,近几年来得到了快速发展.如图是所建的风车阵.如果风车阵中发电机总输出功率为100kW,输出电压是250V,先后经过升压变压器和降压变压器传输到用户,设输电线的总电阻为10Ω.若要求输电线中因发热而损失的功率为输送功率的4%,试求: